(论文)[2022-SIGA-C] Marginal Multiple Importance Sampling

Posted on Edited on In Views:
MMIS 将每一次采样到的策略都认为是一种新策略（可以重复），然后对他们做 balance heuristic MIS，用复杂的计算带来了好的结果；SMIS 只能处理一个参数化的采样方式，但是 MMIS 能够处理多种采样方式；两个应用 path filtering、photon mapping

Marginal Multiple Importance Sampling

  • 作者
    • Rex West：The University of Tokyo Japan
    • Iliyan Georgiev：Autodesk United Kingdom
    • Toshiya Hachisuka：University of Waterloo Canada
  • 使用 MIS 的时候，如果 pdf 无法单点计算【例如是其他 pdf 的积分】，如何处理？
    • SMIS 只能处理一种采样方式【一个连续的 technique space \(\mathcal{T_1}\)】
    • 我们提出 MMIS 能够结合多种采样方式【可以处理多个连续的 technique space】
  • 另外给出了两个应用：path filtering、photon mapping

Introduction

  • CMIS 可以结合无穷多种【不可数也行】采样方式，但是计算代价高；于是其使用 SMIS 近似
    • SMIS 预先采样几种采样技术，然后只对这几种技术做 MIS
    • SMIS is limited to combining samples drawn from techniques that are defined (parameterized) in a single technique space.
      • 他说 SMIS 只能从一个单一的参数化采样方法中采样，MMIS 能够结合多种技术
      • 意思应该是 \(\mathcal{T}_1,\mathcal{T}_2\) 都是无穷的空间，SMIS 只能处理 \(\mathcal{T}_1\)，但是 MMIS 能够结合 \(\mathcal{T}_1,\mathcal{T}_2\)
  • 提出了 MMIS，然后以及几种应用
    • marginal path sampling framework
    • path-space filtering；CMIS 论文说可以将其构建成无偏采样形式
      • 对比 path graph
  • MMIS 和 SMIS 的区别
    • SMIS 只考虑了 1 种采样空间；MMIS 可以和处理多种采样空间
    • SMIS 脱胎于 CMIS，因此本文将 SMIS 的作用限制于只能采样一种采样方式【对应 CMIS 的那个连续空间】
    • 说实话这个扩展也太直观了，以至于我都没理解他在做这个
  • MMIS 的思路：把每一种边缘分布本身当作一种采样策略
    • MMIS 混合的是 \(nT\) 种采样技术
      • 看看副录中平衡启发式的表达形式你就懂了

MMIS

  • 积分

\[ I=\int_{\mathcal{X}}f(x)\;\mathrm{d}x \]

  • \(T\) 种采样技术 ，每种 \(n_i\) 个样本，每个样本采样概率 \(p_i\)
  • 无偏估计如下

\[ \langle I \rangle_{\text{MIS}} = \sum_{i=1}^{T} \sum_{j=1}^{n_i} \frac{w_i(x_{i,j}) f(x_{i,j})}{n_i p_i(x_{i,j})} = \sum_{i=1}^{T} \sum_{j=1}^{n_i} \langle I \rangle_{\text{MIS}}^{i,j} \tag{1} \]

  • \(p_i\) 可能没有闭式解，这样就无法无偏估计 \(I\)

\[ p_i(x) = \int_{\mathcal{T}_i} p_i(x, t) \,\mathrm{d}t = \int_{\mathcal{T}_i} p_i(x \vert t) p_i(t) \,\mathrm{d}t \tag{2} \]

Marginal MIS estimator

  • balance heuristic

\[ w_i(x) = \frac{n_i p_i(x)}{\sum_{i'=1}^{T} n_{i'} p_{i'}(x)} = \frac{n_i p_i(x)}{\sum_{i'=1}^{T} n_{i'} \int_{\mathcal{T}_{i'}} p_{i'}(x \vert t) p_{i'}(t) \,\mathrm{d}t} \tag{3} \]

  • 那么单样本的估计如下

\[ \langle I \rangle_{\text{MIS}}^{i,j} = \frac{f(x_{i,j})}{\sum_{i'=1}^{T} n_{i'} \int_{\mathcal{T}_{i'}} p_{i'}(x_{i,j} \vert t) p_{i'}(t) \,\mathrm{d}t} \tag{4} \]

  • 和 CMIS 类似，分母构建估计

\[ \langle I \rangle_{\text{MIS}}^{i,j} \approx \frac{f(x_{i,j})}{\sum_{i'=1}^{T} \cancel{n_{i'}} \left[ \frac{1}{\cancel{n_{i'}}} \sum_{j'=1}^{n_{i'}} \frac{p_{i'}(x_{i,j} \mid t_{i',j'}) \cancel{p_{i'}(t_{i',j'})}}{\cancel{p_{i'}(t_{i',j'})}} \right]} \tag{5} \]

  • 此时无偏估计如下
    • 条件是采样到的技术需要包含整个定义域【和 SMIS 相同】

\[ \langle I \rangle_{\text{MMIS}} = \sum_{i=1}^{T} \sum_{j=1}^{n_i} \frac{f(x_{i,j})}{\sum_{i'=1}^{T} \sum_{j'=1}^{n_{i'}} p_{i'}(x_{i,j} \mid t_{i',j'})} \tag{6} \]

  • SMIS 的形式如下

\[ \langle I\rangle_{\mathrm{SMIS}}=\sum_{i=1}^n\frac{\dot{w}(t_i,x_i)f(x_i)}{p(x_i|t_i)}=\sum_{i=1}^n\frac{f(x_i)}{\sum_{j=1}^np(x_i|t_j)} \]

\[ \dot{w}(t_{i},x)=\frac{p(x|t_{i})}{\sum_{j=1}^{n}p(x|t_{j})} \]

  • 二者的区别
    • 当 \(T=1\) 的时候，MMIS 退化为 SMIS【看下面实验计算 pdf 评估次数】
  • 无偏条件都是：采样到的技术需要包含整个定义域
  • classical 和 marginal 结合
    • classical technique：扩展 \(p(x\mid t)=p(x)\)
    • 或者将积分拆分为两个部分：classical + marginal

Canonical experiments

  • 一些 2D 实验
  • MMIS\(_n\) 表示每种策略使用 \(n\) 个样本（\(n_i=n\)）
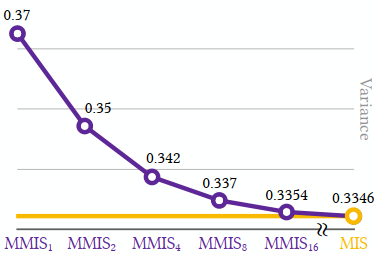
  • 实验 1
    • \(T=2\)，MMIS\(_1\) 能够结合 classical 算法 和 SMIS\(_2\)，然后实现更好的结果
  • 实验 2：一共 \(N\) samples，\(N/(nT)\) 轮取平均
    • MIS 表示式子 (1) 解析计算分母
    • MMIS\(_n\) pdf 评估次数：\(nNT=nT\times nT\times N/(nT)\)
      • 增大了计算开销
    • SMIS\(_n\) pdf 评估次数：\(nN=n^2\times N/n\)

Path Sampling Using MMIS

MCPT

\[ I = \int_{\mathcal{P}} f(\mathbf{\bar{x}}) \,\mathrm{d}\mathbf{\bar{x}} \approx \frac{1}{n} \sum_{i=1}^{n} \frac{f(\mathbf{\bar{x}}_i)}{\rho(\mathbf{\bar{x}}_i)} \tag{7} \]

  • UPT

\[ p(\mathbf{\bar{x}}) = p(x_1, \ldots, x_k) = p(x_1) p(x_2 \mid x_1) \prod_{i=3}^{k} p(x_i \mid x_{i-1}, x_{i-2}) \tag{8} \]

  • 任意方式构建 \(\mathbf{x}\)，只需要 pdf 能解析计算【readily computable】
  • 如下方式：移除 \(\mathbf{x}_2\) 构建，此时 pdf 不好算

\[ \begin{align} p^*(\mathbf{\bar{x}}) &= p^*(\mathbf{x}_1, \mathbf{x}_3, \ldots, \mathbf{x}_{k+1}) \tag{9} \\ &= p^*(\mathbf{x}_1) p^*(\mathbf{x}_3 \mid \mathbf{x}_1) p^*(\mathbf{x}_4 \mid \mathbf{x}_3) \prod_{i=5}^{k+1} p^*(\mathbf{x}_i \mid \mathbf{x}_{i-1}, \mathbf{x}_{i-2}) \tag{10} \\ \\ p^*(\mathbf{x}_3 \mid \mathbf{x}_1) &= \int_{\mathcal{M}} p^*(\mathbf{x}_3 \mid \mathbf{x}_2, \mathbf{x}_1) p^*(\mathbf{x}_2 \mid \mathbf{x}_1) \,\mathrm{d}\mathbf{x}_2 \tag{11} \\ p^*(\mathbf{x}_4 \mid \mathbf{x}_3) &= \int_{\mathcal{M}} p^*(\mathbf{x}_4 \mid \mathbf{x}_3, \mathbf{x}_2) p^*(\mathbf{x}_2 \mid \mathbf{x}_1) \,\mathrm{d}\mathbf{x}_2 \tag{12} \end{align} \]

  • 不能直接 MC 估计 \(p^{\ast}\)，结果有偏
  • MMIS 能解决这个问题

marginal path sampling framework

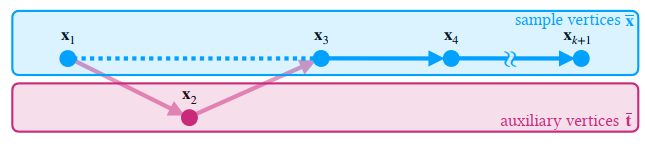
  • 采样得到的路径 \(\mathbf{\bar{x}}\) 依赖于辅助节点 \(\mathbf{\bar{t}}\)
  • 和式子 (6) 中的 MMIS 对应，(6) 中的 \(p_i(x_{i,j} \mid t_{i,j})\) 就是 \(p_i(\mathbf{\bar{x}}_{i,j} \mid \mathbf{\bar{t}}_{i,j})\)
    • classical 情况就是 \(\mathbf{\bar{t}}=\varnothing\)
  • 对于 \(T\) 种采样技术 \(p_i\)，分别采样 \(n_i\) 组 technique-sample 对 \((\mathbf{\bar{x}} \mid \mathbf{\bar{t}})\sim p_i(\mathbf{\bar{x}} \mid \mathbf{\bar{t}})\)，其中 \(\mathbf{\bar{t}\in \mathcal{T}_i}\)
  • marginal path sampling（MPS）estimator 如下
    • 【这里考虑只会删除节点 \(\mathbf{x}_2\)】

\[ \langle I_k \rangle_{\text{MPS}} = \sum_{i=1}^{T} \sum_{j=1}^{n_i} \frac{f(\mathbf{\bar{x}}_{i,j})}{\sum_{i'=1}^{T} \sum_{j'=1}^{n_{i'}} p_{i'}(\mathbf{\bar{x}}_{i,j} \mid \mathbf{\bar{t}}_{i',j'})} \tag{13} \]

  • 这假设 \(p(\mathbf{\bar{x}} \mid \mathbf{\bar{t}})\) 是能计算的，一般都是容易满足的
  • 策略 \(\mathbf{\bar{t}}\) 不一定需要时节点，也可以是波长等

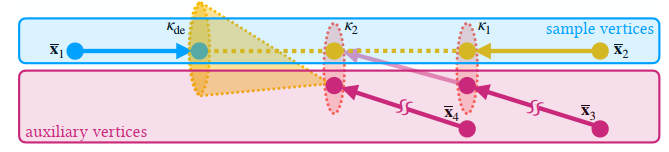
Multi-Vertex Path Filtering

  • CMIS 给出了一种 path filtering 的无偏形式【前缀路径作为 technique，后缀路径作为 sample】

  • MPS 可以处理这个
    • 前缀作为 \(\mathbf{t}\)，\(\mathcal{T}\) 就是所有满足 kernel \(\kappa\) 的前缀路径
    • 当前前缀 + \(\mathbf{t}\) 对应的后缀作为样本 \(\mathbf{x}\)

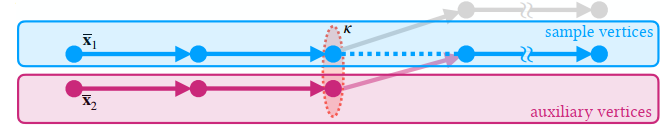
Extension to multi-vertex filtering

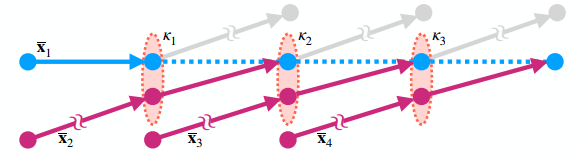
  • 传统的只用一个节点，我们均摊开销，filtering 多个样本
  • 例如下图，3 个节点依次进行采样【\(k=3\)】
    • 看他这个图的意思应该是：根据当前点采样一个 path，再根据采样到的 path 的下一个节点采样
    • 附录里的图就清晰多了

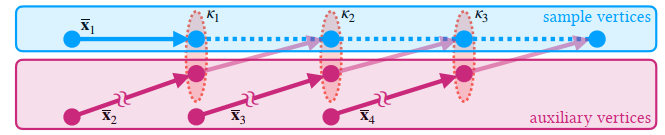
  • 那么采样总数：\(T=\prod_{i=1}^{k}N(\mathbf{P},\kappa_i)\)
    • \(N(\mathbf{P},\kappa_i)\) 表示满足 kernel 的前缀路径数量
    • \(T\) 关于 \(k\) 指数
  • 于是展开 MPS 的分母
    • \(k'\) 表示路径的第 \(k'\) 个节点

\[ \sum_{i'=1}^{T} \sum_{j'=1}^{n_{i'}} p_{i'}(\mathbf{\bar{x}}_{i,j} \mid \bar{t}_{i',j'}) = \sum_{i'=1}^{T} \sum_{j'=1}^{n_{i'}} \underbrace{\prod_{k'=1}^{k} p_{i'}(\mathbf{x}_{i,j,k'} \mid \mathbf{\bar{y}}_{i',j',k'})}_{p_{i'}(\mathbf{\bar{x}}_{i,j} | \mathbf{\bar{t}}_{i',j'})} \tag{14} \]

  • 式子展开之后，有很多公共项，复杂度从指数变为线性，副录有过程

Discussion

  • MPS 无偏条件：对于 \(f(\mathbf{x})>0\) 的点，存在任意一个 \(p_i(\mathbf{x}\mid\mathbf{t})>0\)
    • 选中的采样策略要覆盖定义域
    • 可以通过【including the classical path tracing techniques】实现，【query point 做 pt】
      • 所有策略都无法覆盖定义域时，这样也能实现无偏
  • 无偏实现很复杂，需要对每一个做可见性测试【ray casting】
  • 有偏近似：认为 kernel 内部可见性相同
    • 和 Path Graph 类似，依赖于高效 GPU 实现
  • 和 Path Graph 的区别【还没看 Path Graph 呢】
    • MMIS 在形式上提供了和 MC 的联系，不需要做 energy clamping
    • MMIS 权重和为 1，可以保证无偏
    • 聚类算法需要对每个查询点尽心最近邻查找，然后 pdf 评估，开销巨大；Path Graph 通过 k-means 均摊开销，但是 bias 不可控；我们可控【补充材料】

Result

  • 离谱比赛又来了：CPU ray tracer + cuda GPU filtering
  • 结果：我们用了 multi-vertex 效果好很多
    • SMIS 的 single-vertex 开销大，效果不好

Multi-Vertex Photon Mapping

  • 有些场景 PT 框架下就是效果差，需要 photon mapping【强方向光、焦散】
  • PM 算法：收集周围的 emitter subpaths

  • MPS 框架也适用，只是现在变成了收集 emitter subpath

  • 和之前的 PM 算法实现不兼容，因为他们不是基于 path sampling 的，没存 pdf
  • 实现：作为 PM emitter pass 之后的一个后处理
    • emitter pass -> path filtering（保持方向） -> standard photon-density estimation

Results

  • rendering system 和前面一样
  • 一个强焦散场景的结果：Path Graph < BDPT < PM < Photon Filtering

Conclusion

  • Limitations

    • 有些方式 conditional pdf 也不能算：例如 MCMC

    • 我们的方法引入了额外的内存开销

  • Future work

    • Path and photon filtering 如何结合【类似于 UPS/VCM】
    • 类似于 PM 缩半径，path filtering 能不能也在 kernel 内保持一致
    • MMIS 引入了额外开销
    • 多次复用，形成 Graph

Appedix

MMIS 无偏性证明

  • 采样逻辑等价于：先采样 \(T\) 种技术，才然每种技术分配样本 \(n_i\)
  • 保证了 MIS 和为 1，再加上全覆盖，就是无偏

\[ \begin{align} \mathbb{E}\big[\langle I \rangle_{\text{Mar}}\big] &= \mathbb{E}\big[\langle I \rangle_{\text{Mar}}\big]_{(t_{1,1}, x_{1,1}), \dots, (t_{T,n_T}, x_{T,n_T})} \tag{1a} \\ &= \mathbb{E}\Bigg[\mathbb{E}\big[\langle I \rangle_{\text{Mar}} \big| x_{1,1}, \dots, x_{T,n_T}\big]\Bigg]_{t_{1,1}, \dots, t_{T,n_T}} \tag{1b} \\ &= \mathbb{E}\Bigg[\mathbb{E}\bigg[\sum_{i=1}^T \sum_{j=1}^{n_i} \frac{f(x_{i,j})}{\sum_{i'=1}^T \sum_{j'=1}^{n_{i'}} p_{i'}(x_{i,j} | t_{i',j'})}\bigg]_{x_{1,1}, \dots, x_{T,n_T}}\Bigg]_{t_{1,1}, \dots, t_{T,n_T}} \tag{1c} \\ &= \mathbb{E}\Bigg[\sum_{i=1}^T \sum_{j=1}^{n_i} \int_{\mathcal{X}} \frac{f(x)}{\sum_{i'=1}^T \sum_{j'=1}^{n_{i'}} p_{i'}(x | t_{i',j'})} p_i(x | t_{i,j}) \, \mathrm{d}x\Bigg]_{t_{1,1}, \dots, t_{T,n_T}} \tag{1d} \\ &= \mathbb{E}\Bigg[\int_{\mathcal{X}} \underbrace{\sum_{i=1}^T \sum_{j=1}^{n_i} \frac{p_i(x | t_{i,j})}{\sum_{i'=1}^T \sum_{j'=1}^{n_{i'}} p_{i'}(x | t_{i',j'})}}_{=1} f(x) \, \mathrm{d}x\Bigg]_{t_{1,1}, \dots, t_{T,n_T}} \tag{1e}\\ &= \mathbb{E}\Bigg[\int_{\mathcal{X}} f(x) \, dx\Bigg]_{t_{1,1}, \dots, t_{T,n_T}} = I \tag{1f} \end{align} \]

  • 不一定是从 balance heuristic 推导，只要满足和为 1 就行

\[ \langle I \rangle_{\text{Mar}}^* = \sum_{i=1}^T \sum_{j=1}^{n_i} w_i(t_{i,j}, x_{i,j}) \frac{f(x_{i,j})}{p_i(x_{i,j} | t_{i,j})} \]

  • 使用如下平衡启发式，即得 MMIS estimator

\[ w_i(t, x) = \frac{p_i(x | t)}{\sum_{i'=1}^T \sum_{j'=1}^{n_{i'}} p_{i'}(x | t_{i',j'})} \]

MVPF 实现

  • multi-vertex path filtering（MVPF）

  • 上面的式子 (14)

\[ \sum_{i'=1}^{T} \sum_{j'=1}^{n_{i'}} p_{i'}(\mathbf{\bar{x}}_{i,j} \mid \bar{t}_{i',j'}) = \sum_{i'=1}^{T} \sum_{j'=1}^{n_{i'}} \underbrace{\prod_{k'=1}^{k} p_{i'}(\mathbf{x}_{i,j,k'} \mid \mathbf{\bar{y}}_{i',j',k'})}_{p_{i'}(\mathbf{\bar{x}}_{i,j} | \mathbf{\bar{t}}_{i',j'})} \tag{14} \]

  • 变换形式：预计算好每一种策略的 pdf
    • 复杂度从指数变成线性【指数是因为 \(N(\mathbf{P}, k')\) 这里对 \(k\) 累乘】
    • 感觉思路就是预计算，然后开销分摊给其他的点

\[ \sum_{i'=1}^T \sum_{j'=1}^{n_{i'}} p_{i'}(\bar{x}_{i,j} | \bar{t}_{i',j'}) = \prod_{k'=1}^k \underbrace{\sum_{m=1}^{N(\mathbf{P}, k')} p_m(x_{i,j,k'} | \overline{y}_{m,k'})}_{\text{filter local MIS}} \]

Iterative MVPF 算法

  • 初始化：每一个节点的入射辐射度初始化为原始前缀对应的无偏估计
    • 这在能量上比较稳定，允许任意次数 \(K\) 的迭代
  • 迭代完之后，质量比较高
  • 加入 NEE：相当于加入一种采样策略
    • 每一个节点多加上 \(\mathbf{N}\) 种 Light Sampling 策略
    • path sampling 的时候加上 NEE，cluster filtering 的时候，local MIS 分布修改为

\[ \sum_{m=1}^{N(\mathbf{P}, \kappa_{k'})} p_m(x_{k'} | \overline{y}_{m,k'}) {\color{red}+ N_L(\mathbf{P}, \kappa_{k'}) p_L(x_{k'})} \]

  • Greedy range query clustering
    • 逐个检查是否存在 id，如果没有 id，则执行给定半径的查询，将半径内无 id 的 vertex 和当前 vertex 都设置为新 id