(论文)[2020-SIG] Continuous Multiple Importance Sampling
CMIS
TLDR
- 能够处理无穷多种采样方式的 MIS,处理方式就是先采样 n 种采样技术,采样每个技术分配 1 个样本(NEE 可以理解为一种 n=2 的情况)
- 给了 3 个应用的例子
- Path Reuse
- Spectral Rendering
- Volume Single Scattering
Introduction
- MIS 能结合多种采样技术
- 如何结合 uncountably infinite number (i.e., a continuum) of
techniques?
- 传统的 MIS 理论需要拓展
- 我们将 MIS 泛化到 continuous MIS (CMIS),并给出最优结果(provably optimal balance heuristic)
- 因为最优不容易达到,给出另外一个近似:stochastic MIS (SMIS)
estimator
- 无偏的
- 有效性验证(应用):path space filtering、spectral rendering、volume rendering with photon planes
Background and Related Work
- 积分问题,n 样本 MC 估计
\[ I = \int_{\mathcal{X}}f(x) \mathrm{~d}x,\quad\langle I\rangle_n = \frac{1}{n}\sum_{i=1}^n\frac{f(x_i)}{p(x_i)},\quad(1) \]
- \(p(x)\propto f(x)\) 则方差小
- discrete MIS (DMIS):\(T\) 种采样技术
- 把积分拆分为 \(T\) 个部分
\[ I = \int_{\mathcal{X}} \underbrace{\sum_{t = 1}^Tw_t (x)}_{=1} f(x) \mathrm{~d}x = \sum_{t = 1}^T \underbrace{\int_{\mathcal{X}}w_t (x)f(x) \mathrm{~d}x}_{=I_t} = \sum_{t = 1}^TI_t. (2) \]
- one-sample DMIS estimator
- \(P_t\) 的概率选中积分 \(I_t\)
\[ \langle I\rangle_{\text{DMIS}}=\frac{\langle I_t\rangle_1}{\mathrm{P}_t}=\frac{w_t(x)f(x)}{\mathrm{P}_tp_t(x)}.\quad(3) \]
- multi-sample DMIS estimator(\(n\)
样本)
- \(I_t\) 使用 \(n_t=\mathrm{P}_tn\) 个样本估计
\[ \langle I\rangle_{\text{MDMIS}}=\sum_{t=1}^T\langle I_t\rangle_{n_t}=\sum_{t=1}^T\frac{1}{n_t}\sum_{i=1}^{n_t}\frac{w_t(x_{t,i})f(x_{t,i})}{p_t(x_{t,i})}.\quad(4) \]
- \(w_t(x)\) 任意选择,只需要满足
- \(\sum_{t=1}^{T}w_t(x)=1,\forall f(x)\ne0\)
- \(w_t(x)=0,\forall p_t(x)=0\)
- 平衡启发式(balance heuristic):单样本最优
\[ \hat{w}_t(x)=\frac{\mathrm{P}_tp_t(x)}{\sum_{t'=1}^T\mathrm{P}_{t'}p_{t'}(x)}.\quad(5) \]
- 现有研究
- 研究如何分配样本
- 提高 weighting heuristics
- 利用 domain-specific auxiliary information
- 考虑方差:balance heuristic with variance estimates,
- optimize the sampling densities for balance-heuristic combination
- 多样本的 Optimal MIS(允许权重为负的前提下找到最优 weight function)
- stochastic technique selection
CMIS
- Continuous Multiple Importance Sampling
- DMIS 的扩展
CMIS formulation
- \(\mathcal{T}\):technique space,任意 \(t\in\mathcal{T}\) 都是一种采样策略
- CMIS 的形式如下,其中 \(\int_{\mathcal{T}}w(t,x)\mathrm{~d}t=1,\forall x\in\mathcal{X}\land f(x)\ne0\)
\[ I=\int_{\mathcal{X}}\underbrace{\int_{\mathcal{T}}w(t,x)\mathrm{~d}t}_{=1}f(x)\mathrm{~d}x=\int_{\mathcal{T}}\int_{\mathcal{X}}w(t,x)f(x)\mathrm{~d}x\mathrm{~d}t.\quad(6) \]
- 此时 one-sample MC 估计如下
- \(p(t,x)\):联合分布
\[ \langle I\rangle_{\text{CMIS}}=\frac{w(t,x)f(x)}{p(t,x)}=\frac{w(t,x)f(x)}{p(t)p(x\mid t)}.\quad(7) \]
- 对于 \(w\) 的要求:\(C_1\) 和 \(C_2\)
\[ \begin{aligned} (C_1)\quad&\int_{\mathcal{T}}w(t,x) \mathrm{d}t=1,&\text{whenever } f(x)\neq0.&\quad(8\text{a})\\ (C_2)\quad& w(t,x)=0,&\text{whenever } p(t,x)=0.&\quad(8\text{b}) \end{aligned} \]
- 对于 \(f(x)\ne0\) 的地方,至少存在一个 \(t\) 使得 \(p(t,x)=p(t)p(x\mid t)>0\)
- 最简单的 CMIS 函数:uniform
\[ w_{\text{u}}(t,x)=\frac{1}{\int_{\mathcal{T}}\mathrm{~d}t} \]
- CMIS 版本的平衡启发式(balance heuristic),最优性证明见副录 A
- \(p(x)\) 和 \(p(t)\) 的 \(p\) 不是一个含义,只是都表示概率
- 是 one-sample 最优的平衡启发式的泛化形式
\[ \bar{w}(t,x)=\frac{p(t)p(x|t)}{\int_{\mathcal{T}}p(t')p(x|t') \mathrm{d}t'}=\frac{p(t,x)}{\int_{\mathcal{T}}p(t',x) \mathrm{d}t'}=\frac{p(t,x)}{p(x)}.\quad(9) \]
- 类似的,这也相当于用 \(p(x)\) 对整体进行采样(和 DMIS 相同)
\[ \langle I\rangle_{\mathrm{CMIS}}=\frac{\bar{w}(t,x)f(x)}{p(t,x)}=\frac{\cancel{p(t,x)}f(x)}{p(x)\cancel{p(t,x)}}=\frac{f(x)}{p(x)}.\quad(10) \]
讨论
- 前人的工作:无穷但是可数 \(\aleph_0\),本文允许任意维度 \(\aleph_1,\cdots\)
- 【2019-SIG】Photon surfaces for robust, unbiased volumetric density estimation.
- 将不可数转化为可数
- \(\mathcal{T}\) 离散化,只选取其中若干技术
- 让 \(p(t,x)\) 分段常数
- multi-samples:直接操作不现实(不可数无穷样本),对每个技术 \(t\) 自身平均(\(/n(t)\))
SMIS formulation
- stochastic MIS (SMIS) estimator
- 式子 10
的分母部分可能并没有闭式解(大部分情况下)
- 策略:需要构建 \(1\big/p(x)\)
的无偏估计(倒数的无偏估计)
- 这段话啥意思???
- However, this method requires special care when \(p(x)>1\), which is generally the case as \(p(x)\) is a probability density
- 策略:需要构建 \(1\big/p(x)\)
的无偏估计(倒数的无偏估计)
- 论文给出更简单的估计:初始有偏 -> 转变成无偏
- 采样 \(n\) 个样本对 \((t_i,x_i)\) 用于估计 \(p(x)\),使用式子 9
的平衡启发式
- 此时,估计是有偏的(\(p(x)\) 的无偏估计并不是 \(1\big/p(x)\) 的无偏估计)
\[ \begin{aligned} &\underbrace{\frac{1}{n}\sum_{i=1}^{n}\frac{p(t_{i},x_{i})}{\int_{\mathcal{T}}p(t,x_{i})\mathrm{d}t}\cdot\frac{f(x_{i})}{p(t_{i},x_{i})}}_{n\text{-sample CMIS}}\\ \approx\quad&\underbrace{\frac{1}{n}\sum_{i=1}^{n}\frac{p(t_{i},x_{i})}{\frac{1}{n}\sum_{j=1}^{n}\frac{p(t_{j},x_{i})}{p(t_{j})}}\cdot\frac{f(x_{i})}{p(t_{i},x_{i})}}_{n\text{-sample SMIS approximation}} \end{aligned} \quad(11) \]
- 条件概率展开:\(p(t_i,x_i)=p(t_i)p(x_i\mid t_i)\)
\[ \langle I\rangle_{\mathrm{SMIS}}=\sum_{i=1}^n\frac{\dot{w}(t_i,x_i)f(x_i)}{p(x_i|t_i)}=\sum_{i=1}^n\frac{f(x_i)}{\sum_{j=1}^np(x_i|t_j)} ,\quad(12) \]
\[ \dot{w}(t_{i},x)=\frac{p(x|t_{i})}{\sum_{j=1}^{n}p(x|t_{j})} \]
- \(\langle
I\rangle_{\mathrm{SMIS}}\) 是 \(\langle{I}\rangle_{\text{CMIS}}\)
的有偏估计,但是 \(\langle
I\rangle_{\mathrm{SMIS}}\) 是 \(I\) 的无偏估计
- 核心关键:计算 MIS 的时候只使用了采样得到的 \(n\) 种采样技术,没有管剩余的其他技术
- 在 Proxy Tracing 文章中,考虑了所有的剩余技术
- 整个采样逻辑等价于:先采样 \(n\) 种技术【可重复】,然后每种技术采样一个样本
- 无偏性证明
- 和 DMIS 的区别,使用的技术是先从 \(\mathcal{T}\) 中采样得到的,而不是固定的
- 可以理解为 random DMIS-discretization
- SMIS 的方式有了近似,不再是原始的 balance heuristic,因此不再有方差最小的性质
- \(n^2\) 次 pdf 计算过于复杂,解析解近似(应用 3)
- SMIS 同时兼容了有限、可数情况种采样技术
方差分析
- 没有理论分析,而是进行了实验验证
- 限定:一共采样 \(N\) 个样本
- 含义
- \(\text{SMIS}_{n}\) 表示使用 \(n\) 种技术的 SMIS,\(N/n\) 次实现
- \(\text{CMIS}_{\text{b}}\):balance heuristic 的 CMIS
- \(\text{CMIS}_{\text{u}}\):均匀采样的 CMIS,\(w_{\text{u}}(t,x) = 1/\int_{\mathcal{T}}\mathrm{d}t\)
- 实验:第一行为分布,下面两行为不同的 \(f(x)\) 对应的方差
- \(p(x),p(t)\) 都是边缘分布
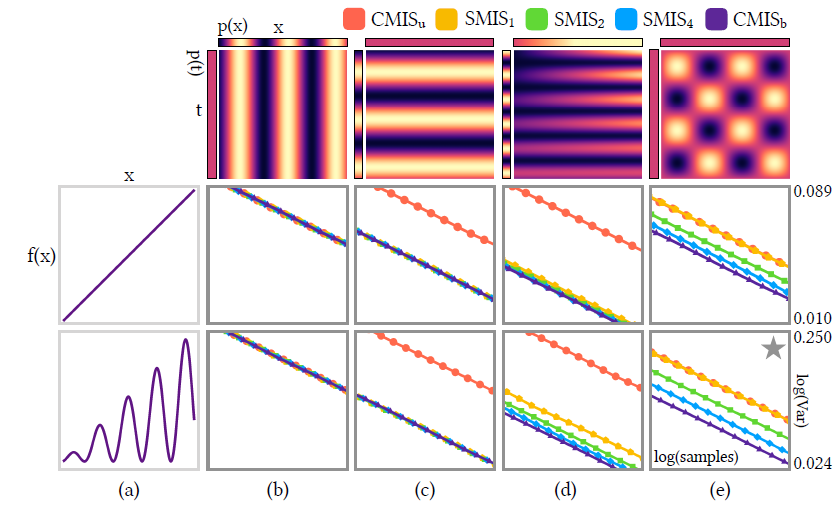
- 图 (b)
- \(p(t)=\text{const}\)
- 结果都一样
- 图 (c)
- \(p(x)\) 相同、\(p(x\mid t)=F(x)\):与 \(t\) 无关
- 除了 \(\text{CMIS}_{\text{u}}\) 最差,其他都一样(处理 \(p(t)\) 的方式相同)
- 图 (d)
- \(p(t)\) 正弦,\(p(x)\) 均匀到线性(程度不同)
- \(\text{CMIS}_{\text{u}}\)
最差,\(\text{CMIS}_{\text{b}}\)
最好,\(\text{SMIS}_{\text{b}}\) 中
\(b\) 越大越好
- \(\text{CMIS}_{\text{u}}<\text{SMIS}_{\text{b}}<\text{CMIS}_{\text{b}}\)
- 图 (e)
- 边缘分布是均匀的,但是 \(p(x\mid x)\) 不是均匀的
- \(\text{CMIS}_{\text{u}}=\text{SMIS}_{\text{1}}<\text{SMIS}_{\text{b}}<\text{CMIS}_{\text{b}}\)
- 结果:上面 \(\star\) 图的结果
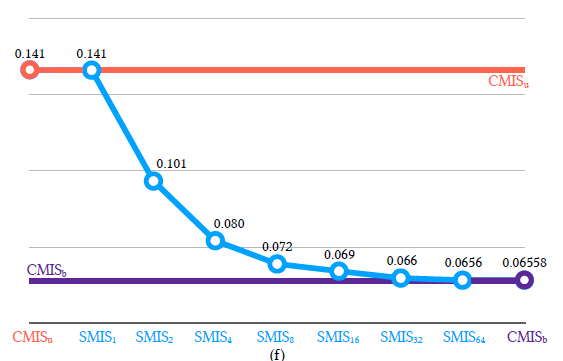
- 在这里,我们是可以计算 \(\text{CMIS}_{\text{b}}\)(式子 9)分母中的积分部分的,因此可以实现 \(\text{CMIS}_{\text{b}}\)
- 最高效率的 SMIS,总采样数(如下)与方差的 trade-off
- \(\text{SMIS}_{\text{n}}\):\(\dfrac{n}{n}\times n^2=n^2\)
- \(\text{SMIS}_{\text{n/2}}\):\(\dfrac{n}{n/2}\times \left(\dfrac{n}{2}\right)^2=\dfrac{n^2}{2}\)
应用1:Path Reuse
- reusing (sub)paths across multiple pixel estimations
- 之前的工作
- Path and (ir)radiance filtering methods:灵活但是引入了 bias
problem statement
- 像素积分
- eye subpath 贡献 \(f_{\text{e}}\),prefix subpaths \(\overline{\mathbf{y}}\)
- light subpath 贡献 \(f_{\text{l}}\), suffix subpaths \(\overline{\mathbf{z}}\)
- 路径 \(\overline{\mathbf{x}}=\mathbf{x}_1\mathbf{x}_2\cdots \in\mathcal{P}=\mathcal{M}^{\infty}\) (路径空间)
- \(\overline{\mathbf{x}}=\overline{\mathbf{yz}}\),我们认为 \(\mathcal{P}\times\mathcal{P}=\mathcal{M}^{\infty}\)(因为路径长度有限)
\[ I=\int_{\mathcal{P}}f(\overline{\mathbf{x}}) \mathrm{d}\overline{\mathbf{x}}=\int_{\mathcal{P}}f_{\mathrm{e}}(\overline{\mathbf{y}})\underbrace{\int_{\mathcal{P}}f_{\mathrm{l}}(\overline{\mathbf{y}},\overline{\mathbf{z}}) \mathrm{d}\overline{\mathbf{z}}}_{I(\overline{\mathbf{y}})} \mathrm{d}\overline{\mathbf{y}}=\int_{\mathcal{P}}f_{\mathrm{e}}(\overline{\mathbf{y}}) I(\overline{\mathbf{y}}) \mathrm{d}\overline{\mathbf{y}},\quad(13) \]
- 需要求 \(I(\overline{\mathbf{y}})\) 的一个无偏估计
\[ \langle I\rangle=\frac{f_\mathbf{e}(\overline{\mathbf{y}})}{p(\overline{\mathbf{y}})}\langle I(\overline{\mathbf{y}})\rangle_n=\frac{f_\mathbf{e}(\overline{\mathbf{y}})}{p(\overline{\mathbf{y}})}\sum_{i=1}^nw(\overline{\mathbf{y}},\overline{\mathbf{z}}_i)\frac{f_\mathbf{l}(\overline{\mathbf{y}},\overline{\mathbf{z}}_i)}{p(\overline{\mathbf{z}}_i)},\quad(14) \]
- splitting:\(p(\overline{\mathbf{z}}_i)=p(\overline{\mathbf{z}}_i\mid
\overline{\mathbf{y}}),w=\dfrac{1}{n}\)
- 效率低:\(\overline{\mathrm{z}}_i\) 关于 \(\overline{\mathrm{y}}\) 是特异化的(不同的 \(\overline{\mathrm{y}}\) 不同)
- 直接连接其他的未分裂路径(下图所示),后缀路径的开销被摊销了,如何计算?
- 现有策略:所有像素得到的后作 DMIS;直接核函数收集末端附近的后缀路径(biased)
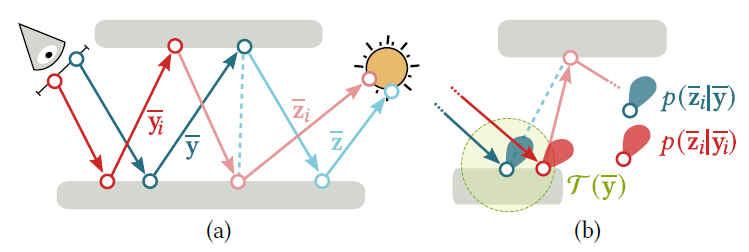
CMIS formulation
- \(\overline{\mathbf{y}}\) 作为 technique, \(\overline{\mathbf{z}}_i\) 作为样本
\[ I(\overline{\mathbf{y}})=\int_{\mathcal{P}}\underbrace{\int_{\mathcal{T}}w(\overline{\mathbf{y}}^{\prime},\overline{\mathbf{z}}) \mathrm{d}\overline{\mathbf{y}}^{\prime}}_{=1}f_1(\overline{\mathbf{y}},\overline{\mathbf{z}}) \mathrm{d}\overline{\mathbf{z}}=\int_{\mathcal{T}}\int_{\mathcal{P}}w(\overline{\mathbf{y}}^{\prime},\overline{\mathbf{z}}) f_1(\overline{\mathbf{y}},\overline{\mathbf{z}}) \mathrm{d}\overline{\mathbf{z}}\mathrm{d}\overline{\mathbf{y}}^{\prime},\quad(15) \]
- 和之前的 CMIS 部分类似,我们可以构建 CMIS、SMIS 估计子
算法
- Practical path-space filtering algorithm
- \(\text{SMIS}_{\text{n}}\) 需要 \(n^2\) 次可见性测试,\(\sum\) 中有 \(n\times\),\(w\) 求解需要 \(n\) 次
- 加速:限制 \(\mathcal{T}\) 的范围在原始前缀路径末端顶点附近
- biased 近似:认为一直可见,认为光子路末端顶点的 BSDF 不变
- 近似原因:都在原始前缀末端顶点的附近
- 不用可见性测试,同时不需要重新计算 BSDF 函数
实现
- two-stage algorithm
- 1:1spp 路径,然后将他们的顶点保存在 hashed spatial grid 中
- 2:对于每一个 \(\overline{\mathbf{y}}\),我们搜集其末端顶点周围的顶点构成技术
\(\mathcal{T}\),构建 SMIS 估计
- 采样 \(\overline{\mathbf{y}}_i\in \mathcal{T}\),然后将将 \(\overline{\mathbf{y}}\) 和 \(\overline{\mathbf{z}}_i\) 连接,进行估计计算
- 搜索半径:6spp in screen space(换算)
- 随着时间进行减小
- 评估:SMAPE(symmetric mean absolute percentage error)
- reference and estimated value
\[ E=\frac{1}{P}\sum_{i=1}^{P}\frac{|r_{i}-e_{i}|}{|r_{i}|+|e_{i}|} \]
- 对比:同时间、同样本都有
- Path Space Filtering(Keller 2014)
- 相关性问题
应用2:Spectral Rendering
\[ I=\int_{\mathcal{P}}\int_{\Lambda}f(\overline{\mathbf{x}},\lambda)\mathrm{~d}\lambda\mathrm{d}\overline{\mathbf{x}}=\int_{\mathcal{S}}f(\overline{\mathbf{s}})\mathrm{~d}\overline{\mathbf{s}}, \]
- Wilkie 2014:Hero Wavelength Spectral Sampling
- 每条路径携带多个波长,每次选择一个波长作为 \(\lambda_h\)(hero
wavelength),生成散射光线
- 多个波长是等间隔分布(如图 7)
- 为什么可以这么做:大多数路径都和波长无关
- 遇到 spectral power distributions(SPDs)时,能量集中在特定波长位置,效果不好,例如荧光灯
- 每条路径携带多个波长,每次选择一个波长作为 \(\lambda_h\)(hero
wavelength),生成散射光线
\[ \langle I\rangle_{\text{HeroMIS}}=\sum_{i=1}^{n}\frac{f(\overline{\mathbf{x}},\lambda_{i})}{\sum_{j=1}^{n}p(\lambda_{j})p(\overline{\mathbf{x}}|\lambda_{j})}.\quad(19) \]
CMIS formulation
\[ I=\int_{\mathcal{S}}\underbrace{\int_Tw(\xi,\overline{\mathbf{s}}) \mathrm{d}\xi}_{=1}f(\overline{\mathbf{s}}) \mathrm{d}\overline{\mathbf{s}}, \]
- 采样的时候,要求路径重用:\(\mathbf{\overline{s}}_{i}=\{\mathbf{\overline{x}},\lambda_{i}\}\),和
Hero 的区别在于我们在波长选择上更自由
- 这不就是一个重要性采样吗
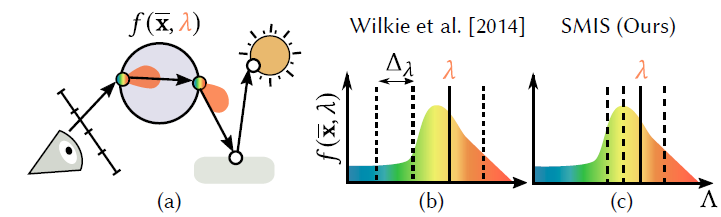
实现
- 图片:RGB -> sRGB -> spectral
- CIE 1931 standard observer chromatic response curves
- 2019 Jakob
- 实现
\[ p(\overline{\mathbf{s}}|\xi)=p(\overline{\mathbf{x}},\lambda)=p(\lambda)p(\overline{\mathbf{x}}|\lambda) \]
- \(p(\lambda)\):正比于如下两个量的乘积,然后使用分层的模式进行采样
- the observer response
- a mixture of the scenes’ light-source SPDs
- 分层:We use a stratified sample pattern that is warped according to
that PDF
- 好像没仔细说?
- 对比算法:除了 uniform 都使用 \(p(\lambda)\),不说明都采样 4 个波长
- \(\text{SMIS}\)(论文)、\(\text{SMIS}_{\text{i}}\)(不分层)、brute-force(\(\text{CMIS}\),直接对 512 个波长进行计算)
- HeroMIS(\(p(\lambda)\) 采样主波长)
- 只采样一个波长:Uniform(均匀采样波长)、SpectralIS
- 感觉提升就是:重要性采样好于普通采样
应用3:Volume Single Scattering(没看懂)
- volumetric light transport simulation
Problem statement
- Deng 2019 提出了 photon planes,用于求解矩形光源、单次散射的的体渲染
- phone plane:给定光源上的线段 \(e\),采样出射方向 \(\omega_l\)
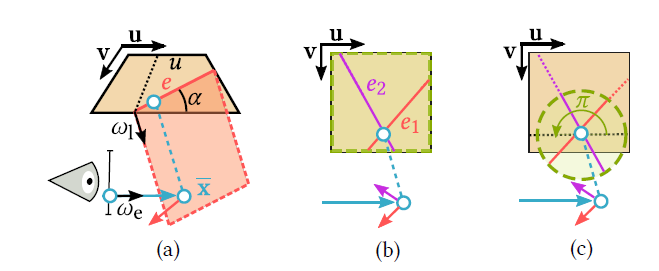
- A primary ray shot from the camera gathers contribution from a given photon plane if it intersects it.
- 线段:\(e=(u,\alpha)\in\mathbb{R}\times[0,\pi]\)
- 采样技术:\(\mathcal{T}\) 就是采样
\(e\)
- 问题:ray 和 photon plane 平行?此时需要 MIS 考虑所有可能性
\[ \langle I\rangle_e=\frac{f(\overline{\mathbf{x}})}{p(\overline{\mathbf{x}}|e)}.\quad(22) \]
CMIS Formulation
\[ I=\int_{\mathcal{P}}f(\overline{\mathbf{x}})\mathrm{d}\overline{\mathbf{x}}=\int_{\mathcal{T}}\int_{\mathcal{P}}w(e,\overline{\mathbf{x}})f(\overline{\mathbf{x}})\mathrm{~d}\overline{\mathbf{x}}\mathrm{d}e,\quad(23) \]
- CMIS
\[ \langle I\rangle_{\text{CMIS}}=\frac{\bar{w}(e,\overline{\mathbf{x}})f(\overline{\mathbf{x}})}{p(e,\overline{\mathbf{x}})},\quad\text{with}\quad\bar{w}(e,\overline{\mathbf{x}})=\frac{p(e,\overline{\mathbf{x}})}{\int_{\mathcal{T}}p(e',\overline{\mathbf{x}}) \mathrm{d}e'}.\quad(24) \]
- 这里往后就都不是太懂了?主要不太懂流程?得看看 Deng2019 的论文
- 式子转换:式子 25
- \(p(e)=C\) ,是常数,均匀采样?
\[ p(e,\overline{\mathbf{x}})=p(e)\cdot p(\overline{\mathbf{x}}|e)=C\cdot p(\overline{\mathbf{x}}) \underbrace{|(e\times\omega_1)\cdot\omega_\mathrm{e}| }_{J(e,\overline{\mathbf{x}})} \]
- 假设:the photon plane width does not change with orientation
- \(\Vert{e}\Vert\) 相同,\(\mathbf{u},\mathbf{v}\) 对光源边长归一化
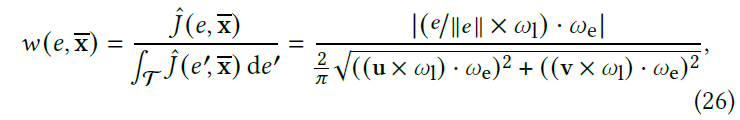
- SMIS:不近似 \(J\),而是先采样若干技术
副录
平衡启发式最优
- 证明和离散类似
- 首先推导方差形式如下
\[ \begin{aligned} \mathbb{V}[\langle I\rangle_{\text{CMIS}}] &=\mathbb{E}\big[\langle I\rangle_{\text{CMIS}}^{2}\big]-\mathbb{E}\big[\langle I\rangle_{\text{CMIS}}\big]^{2}&(28\mathrm{a})\\ &=\int_{\mathcal{X}}\int_{\mathcal{T}}\frac{w^{2}(t,x)f^{2}(x)}{p(t,x)}\mathrm{~d}t\mathrm{~d}x-I^{2}.&(28\mathrm{b}) \end{aligned} \]
- 找到 \(w\)
最小化方差,就是最小化如下式子
- 第一个等号:外层与 \(w\) 无关
- 第二个等号:积分与 \(f(x)\) 无关
\[ \bar{w}=\underset{w}{\operatorname*{argmin}}\bigg[\int_{\mathcal{T}}\frac{w^2(t,x)f^2(x)}{p(t,x)}\mathrm{d}t\bigg]=\underset{w}{\operatorname*{argmin}}\bigg[\int_{\mathcal{T}}\frac{w^2(t,x)}{p(t,x)}\mathrm{d}t\bigg],\quad(29) \]
证明
- 带约束的优化问题(chatgpt)
\[ \underset{w}{\operatorname*{argmin}} \left[ \int_{\mathcal{T}} \frac{w^2(t)}{p(t)} \mathrm{d}t \right] \]
- 约束条件
\[ \int_{\mathcal{T}} w(t) \, \mathrm{d}t = 1 \]
引入拉格朗日乘子法
- 首先定义拉格朗日函数如下,其中 \(\lambda\) 是拉格朗日乘子
\[ \mathcal{L}[w, \lambda] = \int_{\mathcal{T}} \frac{w^2(t)}{p(t)} \mathrm{d}t + \lambda \left( \int_{\mathcal{T}} w(t) \, \mathrm{d}t - 1 \right) \]
计算拉格朗日函数的变分
- 引入扰动函数 $ (t) $,并考虑 $ w(t) $ 的变分
\[ w(t) \rightarrow w(t) + \epsilon \eta(t) \]
- 拉格朗日函数的变分为
\[ \mathcal{L}[w + \epsilon \eta, \lambda] = \int_{\mathcal{T}} \frac{(w(t) + \epsilon \eta(t))^2}{p(t)} \mathrm{d}t + \lambda \left( \int_{\mathcal{T}} (w(t) + \epsilon \eta(t)) \, \mathrm{d}t - 1 \right) \]
- 展开并计算一阶条件
\[ \mathcal{L}[w + \epsilon \eta, \lambda] = \int_{\mathcal{T}} \left( \frac{w^2(t)}{p(t)} + \frac{2\epsilon w(t) \eta(t)}{p(t)} + \frac{\epsilon^2 \eta^2(t)}{p(t)} \right) \mathrm{d}t + \lambda \left( \int_{\mathcal{T}} w(t) \, \mathrm{d}t - 1 \right) + \epsilon \lambda \int_{\mathcal{T}} \eta(t) \, \mathrm{d}t \]
- 忽略二阶小量 \(\epsilon^2\) 项,得到
\[ \mathcal{L}[w + \epsilon \eta, \lambda] \approx \int_{\mathcal{T}} \frac{w^2(t)}{p(t)} \mathrm{d}t + \epsilon \int_{\mathcal{T}} \frac{2 w(t) \eta(t)}{p(t)} \mathrm{d}t + \lambda \left( \int_{\mathcal{T}} w(t) \, \mathrm{d}t - 1 \right) + \epsilon \lambda \int_{\mathcal{T}} \eta(t) \, \mathrm{d}t \]
- 要求该函数在 \(\epsilon = 0\) 处的一阶导数为零
\[ \frac{\mathrm{d}}{\mathrm{d}\epsilon} \mathcal{L}[w + \epsilon \eta, \lambda] \bigg|_{\epsilon=0} = \int_{\mathcal{T}} \frac{2 w(t) \eta(t)}{p(t)} \mathrm{d}t + \lambda \int_{\mathcal{T}} \eta(t) \, \mathrm{d}t = 0 \]
消去扰动函数
- 由于 \(\eta(t)\) 是任意函数,这意味着系数必须为零
\[ \frac{2 w(t)}{p(t)} + \lambda = 0 \]
- 因此,我们得到
\[ w(t) = -\frac{\lambda p(t)}{2} \]
确定拉格朗日乘子
- 利用约束条件 \(\int_{\mathcal{T}} w(t) \, \mathrm{d}t = 1\),我们可以求解 \(\lambda\):
\[ \int_{\mathcal{T}} -\frac{\lambda p(t)}{2} \, \mathrm{d}t = 1\implies \lambda = -\frac{2}{\int_{\mathcal{T}} p(t) \, \mathrm{d}t } \]
得到最优解
\[ \boxed{w(t) = \frac{p(t)}{\int_{\mathcal{T}} p(t) \, \mathrm{d}t}} \]
SMIS 无偏性
- 整个采样逻辑等价于:先采样 \(n\)
种技术【可重复】,然后每种技术采样一个样本【33a 到 33b
其实就是独立,才能变换】
- NEE 类似,确定两种(\(n=2\))技术,然后各分配一个样本
- 更像是:\(p(t_i)\cdot\frac{1}{n}\cdot p(x_i\mid t_i)\)
\[ \begin{aligned} \mathbb{E}[\langle I\rangle_{\mathrm{SMIS}}] & =\mathbb{E}\Big[\langle I\rangle_{\mathrm{SMIS}}\Big]_{(t_{1},x_{1}),...,(t_{n},x_{n})} & \text{(33a)} \\ &=\mathbb{E}\Big[\mathbb{E}\Big[\langle I\rangle_{\text{SMIS}}\Big]_{x_{1},...,x_{n}}\Big]_{t_{1},...,t_{n}}& \text{(33b)} \\ &=\mathbb{E}\left[\mathbb{E}\left[\sum_{i=1}^{n}\dot{w}(x_{i},t_{i})\frac{f(x_{i})}{p(x_{i}|t_{i})}\right]_{x_{1},...,x_{n}}\right]_{t_{1},...,t_{n}}& \text{(33c)} \\ &=\mathbb{E}\left[\underbrace{\sum_{i=1}^{n}\int_{\mathcal{X}}\dot{w}(x,t_{i})\frac{f(x)}{\cancel{p(x|t_{i})}}\cancel{p(x|t_{i})} \mathrm{~d}x}_{=\sum_{i=1}^{n}I_{t_{i}}=I}\right]_{t_{1},...,t_{n}}= I& \text{(33d)} \end{aligned} \]
- 条件是采样到的 \(n\) 种技术【可重复】,需要包含整个定义域