(论文)[2025-EGSR] Neural Resampling with Optimized Candidate Allocation
NRIS
- 作者:Rath Alexander【EARS 作者】、Manzi Marco
- Disney Research | Studios, Switzerland
- large-scale CPU renderers,网络训练用
GPU,推理用 CPU
- 不好转 GPU 的原因:massive code-bases, intricate architectures, and
substantial memory requirements
- 不好转 GPU 的原因:massive code-bases, intricate architectures, and
substantial memory requirements
- 学习 5-dimensional unnormalized
incident radiance field,然后重采样 radiance x
BSDF
- 这样的设计允许 neural caching
- 优化 spatially-varying candidate counts 实现最大化效率
- EARS 的框架
- 定位在 path guiding,之前的方法要么慢要么表达能力不足,我们先用网络缓存 radiance,然后重采样,实现又好又快的 path guiding
- 【唉,撞 idea 了,不过毕竟是 EARS 的后续】
Introduction
- PT
- modern CPU hardware can reach hundreds of core hours per frame in complex production scenes
- 我们将入射辐射场建模为:non-parametric, nonsampleable neural model
- 表达能力比参数化模型更好
- 同时可以用于其他任务:radiance caching
- 网络训练推理会带来额外开销
- 大规模 CPU renderer:训练用 GPU,推理用 CPU
- 不需要重新设计 renderer 底层逻辑
- 测试:large-scale production scenes
- 贡献
- 提出非参数化不可采样的 path guiding 算法,RIS 实现
- 给出最优 RIS 次数的数学框架
- 大规模工业场景测试
BackGround & Related Work
- Monte Carlo Light Transport
- Importance sampling
- 限制:采样 pdf 需要解析存在,或者能够算 CDF
- Resampled Importance Sampling(RIS)
- 目的:生成样本近似 \(\hat{p}\)
- 流程:先通过 \(p\) 采样 \(c\) 个样本 \(x_i\);然后根据权重 \(w(x_i)=\hat{p}(x_i)\Big/ q(x_i)\) 重采样
- 无偏估计如下
- 无偏条件:\(\hat{p}>0\Rightarrow \langle f; c \rangle>0\)【覆盖定义域】
- \(1/c\) 是 MIS
\[ \langle f; c \rangle = f(x_s) W_{\text{RIS}},\; W_{\text{RIS}} = \frac{1}{c \hat{p}(x_s)} \sum_{i=1}^{c} w(x_i) \tag{4} \]
- Path guiding
- 试图近似 \(L_{\text{i}}\) 或者 \(L_{\text{i}}\times \text{BSDF}\)
- \(p(\omega_i\mid x)\) 或者 \(p(\omega_i\mid x,\omega_o)\)【5D / 7D】
- 使用之前迭代轮信息近似 \(L_{\text{i}}\)
- 【CVM-2020】A practical path guiding method for participating media
- 学习 incident radiance field + RIS 重采样结合 BSDF response
- 好处是更容易采样,比之前的方式更高效
- 大部分都是细分场景,学习一个 5D 结构,然后认为内部 radiance
分布相同,使用 2D 分布近似
- 不连续性问题:Parallax-Aware 、SDMM 试图解决,但还是存在
- Neural Sampling
- NPM 能快速采样、评估,但是表示能力不足
- NIS、NCV 表示能力强,但是训练推理慢
- 我们的方法:快 + 表示能力强
Neural Resampling
- 学习 incident radiance field:5d【pos、dir】 -> 3d【color】
- 不需要能够采样、不需要归一化【容易训练】
- 另外:还可以用于 Neural Radiance Caching
- 流程如下图
- 迭代训练:训练 GPU,推理 CPU
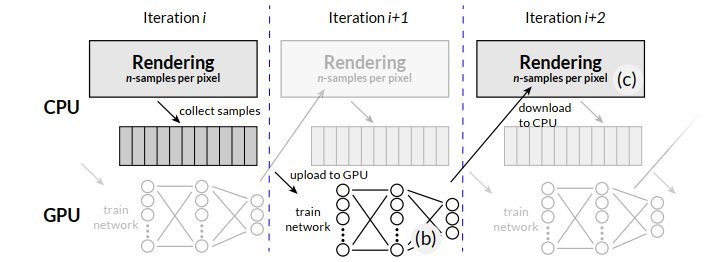
- MLP:\(\mathcal{N}_{\Theta}(\omega_i, x)\)
- 目标分布 \(\hat{p}\) 就是整条光路的贡献【参考了 EARS】【RGB 取平均】
\[ \hat{p}(\omega_i \mid \omega_o, \bar{x}) = \frac{1}{3} \sum_{c \in \{ \text{R}, \text{G}, \text{B} \}} T^c(\bar{x}) B^c(\omega_i \mid x, \omega_o) \mathcal{N}_{\Theta}^c(\omega_i, x) \tag{6} \]
Source Distribution
- source distribution \(q\)
- 权衡学习 guiding 的成本和质量
- 比只使用 \(p_{\text{B}}\) RIS 样本数更少,更快
\[ q(\omega_i \mid x) = \frac{1}{2} p_{\text{G}}(\omega_i \mid x) + \frac{1}{2} p_{\text{B}}(\omega_i \mid x) \tag{7} \]
Defensive Resampling
- 问题:可能会忽略 hard-to-find light source【一块来网络缓存 radiance
准确性】
- MIS 可以解决,但是 RIS 的 pdf 未知【其实感觉 SMIS 的思路 ok】
- 解决:所有可能的采样方向加上一个常数
- 不行,因为实际场景 radiance 大小变化大
- 目标分布加上 defensive target \(\hat{p}_2\)
- \(\hat{p}_1\):上面提到的
- \(\hat{p}_2\):\(q\)
\[ w'(x_i) = \alpha \frac{c \hat{p}_1(x_i)}{\sum_{j=1}^{c} \hat{p}_1(x_j) q^{-1}(x_j)} + (1 - \alpha) \frac{c \hat{p}_2(x_i)}{\sum_{j=1}^{c} \hat{p}_2(x_j) q^{-1}(x_j)} \tag{8} \]
- \(\alpha=0.9\) 很好的平衡了
exploration and exploitation
- \(\alpha\) 概率使用 \(\hat{p}_1\)
Optimized Resampling Candidate Allocation
- RIS 种样本数量的选择很重要
- mitsuba0.6 的测试结果,同时间测试
- \(q\):BSDF 采样
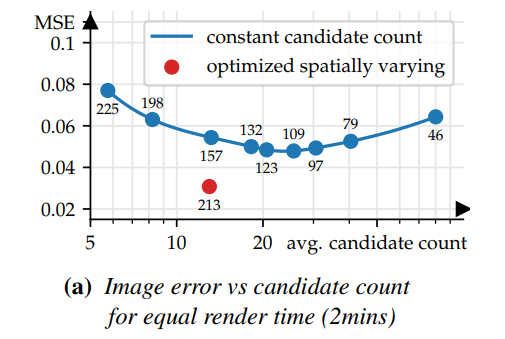
- 【EG-2005】Importance resampling for global illumination
- 确定了单个目标函数的最优采样数
- 我们需要联合优化所有的
- 参考 EARS 的框架
Optimazion Goal
- 最大化效率
\[ c^{\star} = \arg\max_{c} \left( \underbrace{\left( \sum_{\mathrm{px}} \mathbb{C}[\langle I_{\mathrm{px}}; c \rangle] \right)}_{\mathbb{C}_I} \underbrace{\left( \sum_{\mathrm{px}} \mathbb{V}[\langle I_{\mathrm{px}}; c \rangle] \right)}_{\mathbb{V}_I} \right)^{-1} \tag{9} \]
Fixed Point Scheme
- 转化为偏导数为 0
\[ \mathbb{V}_I \frac{\partial}{\partial c(\bar{x})} \mathbb{C}[\langle L_{\text{r}}(\bar{x}); c(\bar{x}) \rangle] + \mathbb{C}_I T^2(\bar{x}) \frac{\partial}{\partial c(\bar{x})} \mathbb{V}[\langle L_{\text{r}}(\bar{x}); c(\bar{x}) \rangle] = 0 \tag{10} \]
- RIS variance
- \(s\):source distribution
- \(t\):target distribution
\[ \mathbb{V}[\langle L_{\text{r}}; c \rangle] = \frac{1}{c} \mathbb{V}_s[\langle L_{\text{r}} \rangle] + \left( 1 - \frac{1}{c} \right) \mathbb{V}_t[\langle L_{\text{r}} \rangle] \tag{11} \]
- RIS cost
- \(K_0\):1 次重采样的开销
- \(K_1\):为 RIS 预计算的一次性开销
- 注意这里的
- RIS 最终样本数为 1,因此不需要局部 cost 的估计【和 RRS 的分裂不同】
\[ \mathbb{C}[\langle L_{\text{r}}; c \rangle] = c K_0 + K_1 + \mathbb{C}[\langle L_{\text{r}} \rangle]\tag{12} \]
- \(\mathbb{C}[\langle L_{\text{r}}; c \rangle]\) 可能不一样,因为 \(c\) 不一样的话,RIS 计算权重不一样【没有闭式解,这里近似为常数】
- 于是求解式子 (9),得到不动点迭代算法
- 当根号内为负数的时候,说明 RIS 不如 source sampling,直接使用 source sampling
\[ c(\bar{x}) = \sqrt{ \frac{T^2(\bar{x}) \left( \mathbb{V}_s[\langle L_{\text{r}}(\bar{x}) \rangle] - \mathbb{V}_t[\langle L_{\text{r}}(\bar{x}) \rangle] \right)}{\mathbb{V}_I} \frac{\mathbb{C}_I}{K_0} } \tag{13} \]
- 具体使用 \(c\):stochastic rounding
- 需要的统计量:全局方差开销,局部二阶矩
- 图片整体的估计:\({\mathbb{V}_I}\)【通过二阶矩、期望转换】、\({\mathbb{C}_I}\)【光线数】
- 局部统计量:方差的差就是二阶矩的差【无偏一阶矩相同】
- 式子 11 的变形如下
\[ \mathbb{M}[\langle L_{\text{r}}; c \rangle] = \frac{1}{c} \mathbb{M}_s[\langle L_{\text{r}} \rangle] + \left( 1 - \frac{1}{c} \right) \mathbb{M}_t[\langle L_{\text{r}} \rangle] \tag{11-M} \]
- RIS 估计:\(\omega_i\)
为重采样得到的方向
- \(W_{\text{RIS}}\) 是 \(p_{\text{RIS}}^{-1}\) 的无偏估计
\[ \langle L_{\text{r}}(\bar{x}); c \rangle = W_{\text{RIS}} \langle L_{\text{r}}(\bar{x}, \omega_j) \rangle \tag{15} \]
- 二阶矩估计如下【source distribution】
- 根据采样过程确定的
\[ \mathbb{E}_{\omega_i \sim p_{\text{RIS}}} \left[ W_{\text{RIS}} \frac{\langle L_{\text{r}}^2(\bar{x}, \omega_i) \rangle}{q(\omega_i \mid \bar{x})} \right] = \mathbb{M}_s[\langle L_{\text{r}} \rangle] \tag{16} \]
- 我们不知道【target distribution】
- 但是我们知道最终结果,RIS estimator 估计最终结果【式子 11 的左边项】
\[ \mathbb{E}_{\omega_i \sim p_{\text{RIS}}} \left[ W_{\text{RIS}}^2 \langle L_{\text{r}}^2(\bar{x}, \omega_i) \rangle \right] = \mathbb{M}[\langle L_{\text{r}}; c \rangle] \tag{17} \]
- 于是根据式子 11 的变形(11-M),可以算出【target distribution】
\[ \mathbb{M}_t[\langle L_{\text{r}} \rangle] = \frac{c \mathbb{M}[\langle L_{\text{r}}; c \rangle] - \mathbb{M}_s[\langle L_{\text{r}} \rangle]}{c - 1} \tag{18} \]
- 变化量就是 16 和 18 的差
\[ \langle \mathbb{V}_s[\langle L_{\text{r}} \rangle] - \mathbb{V}_t[\langle L_{\text{r}} \rangle] \rangle = \frac{c}{c - 1} W_{\text{RIS}} \langle L_{\text{r}}^2(\bar{x}, \omega_i) \rangle \left( \frac{1}{q} - W_{\text{RIS}} \right) \tag{19} \]
- 于是我们只需要缓存 \(L_{\text{r}}^2\),这个可以通过空间树结构+方向结构实现
- RIS 可能变差,我们要检测这样的情况
- 只有在能够提升效率的情况下【被 source sampling \(p\) 相比】,才使用 RIS
- 不是特别理解这个不等式?
- 这里的 variance 是考虑路径,但是 cost 是不考虑的
\[ \left( \mathbb{V}_I + {\color{red}T^2}\mathbb{V}[\langle L_r; c \rangle] \right) \left( \mathbb{C}_I + \mathbb{C}[\langle L_r; c \rangle] \right) < \left( \mathbb{V}_I + {\color{red}T^2}\mathbb{V}_s[\langle L_r \rangle] \right) \left( \mathbb{C}_I + \mathbb{C}_s[\langle L_r \rangle] \right) \tag{20} \]
- 感觉这样更好?因为都是基于 RIS,然后考虑当前节点不使用 RIS
- 感觉也怪怪的,因为 base 不一定是全用 RIS【都可以推导得到式子 21,忽略高阶累乘结果一样了】
- 还是说 \(\mathbb{V}_I\) 应该换成 \(\mathbb{V}_I-\mathbb{V}_{\text{px}}\)【去掉当前路径对应的像素,\(\mathbb{C}_I\) 同理】【?】
\[ \left( \mathbb{V}_I \right) \left( \mathbb{C}_I + \mathbb{C}[\langle L_r; c \rangle] \right) < \left( \mathbb{V}_I - {\color{red}T^2}\mathbb{V}[\langle L_r; c \rangle] + {\color{red}T^2}\mathbb{V}_s[\langle L_r \rangle] \right) \left( \mathbb{C}_I + \mathbb{C}_s[\langle L_r \rangle] \right) \]
- 近似:global 是和,因此大很多,忽略低阶项累乘
\[ \mathbb{V}_I \mathbb{C}[\langle L_r; c \rangle] + \mathbb{C}_I T^2 \mathbb{V}[\langle L_r; c \rangle] < \mathbb{V}_I \mathbb{C}_s[\langle L_r \rangle] + \mathbb{C}_I T^2 \mathbb{V}_s[\langle L_r \rangle] \tag{21} \]
- 进一步推导得到
\[ c>\sqrt{\frac{K1}{K_0}} \]
- 只有满足如上关系才使用 RIS,否则不使用
- 推导
$$ \[\begin{align} \Leftrightarrow & \ T^2 \frac{\mathbb{V}[\langle L_r; c \rangle] - \mathbb{V}_s[\langle L_r \rangle]}{\mathbb{V}_I} + \frac{\mathbb{C}[\langle L_r; c \rangle] - \mathbb{C}_s[\langle L_r \rangle]}{\mathbb{C}_I} < 0 \\ \Leftrightarrow & -\left( 1 - \frac{1}{c} \right) T^2 \frac{\mathbb{V}_s[\langle L_r \rangle] - \mathbb{V}_t[\langle L_r \rangle]}{\mathbb{V}_I} + \frac{\mathbb{C}[\langle L_r; c \rangle] - \mathbb{C}_s[\langle L_r \rangle]}{\mathbb{C}_I} < 0 \\ \Leftrightarrow & -\left( 1 - \frac{1}{c} \right) \underbrace{T^2 \frac{\mathbb{V}_s[\langle L_r \rangle] - \mathbb{V}_t[\langle L_r \rangle]}{\mathbb{V}_I} \frac{\mathbb{C}_I}{K_0}}_{= c^2} + \underbrace{\frac{\mathbb{C}[\langle L_r; c \rangle] - \mathbb{C}_s[\langle L_r \rangle]}{K_0}}_{= c + \frac{K_1}{K_0}} < 0 \end{align}\] $$
这感觉方程也算错了啊,应该是:\(c^2-2c>K_1/K_0\)
如果不使用 RIS 会导致迭代不更新,无法估计 variance delta,于是我们将最小值 clamp 到1-2之间的一个数【1.125】,让部分样本继续 RIS
实现
- Walt Disney Animation Studio’s CPU production renderer Hyperion
Pipeline
- 初始 1 path per pixel,然后几何增长到 16 paths per pixel
- 数据收集:动态调节比例,~4 paths per pixel
- 9 floats:radiance、pos、dir
- ~3.5 G,1920 x 804
- 编码和流程如下图
- 编码
- One-Blob(8 bins)
- HashGrid(8 levels 4 features,分辨率 8 -> 2048)
- MLP:3 x 64,ReLU
- Adam:lr(1e-3 decays to 1e-5)
- 样本:维护一个 ring buffer(FIFO),避免过拟合最近样本,使用 24 spp 样本
- 编码
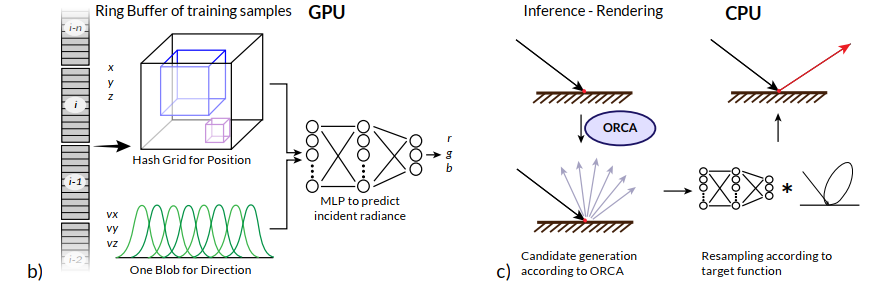
- CPU 推理:优化的 Eigen
- source distribution:Robust fitting of parallax-aware mixtures for path guiding【SIG-2020】【本文后续称他为 VMM】
- 缓存:spatial KD-tree
实验
- 32 threads on an AMD EPYC 7763 server CPU + an Nvidia RTX 4090 GPU
- RR:albedo based
- PG 的时候减小 DI 的方向
- 论文设备:\(K_0=0.01,K_1=0.04\)
- 对比实验
- NPM、NIS 学习 product 的时候,小场景占优;测试场景中,学习 radiance,我们一致的好
- VMM
- VMM + 8 RIS + tree cache
- 测试场景:工业场景光传输简单、焦散少、光源简单;几何、材质复杂
- 测试:相比 PT
- VMM+RIS:25% speedup
- Ours:77%
Future
- 我们估计了 incident radiance
- 使用相同数据结构结合 RR、Radiance Caching 可能是个好方向
- 可以应用在其他方面,例如体的深度采样、DI 采样
- RIS 和 Low-Discrepancy Sampling 结合
- 限制最大深度,导致 incident radiance 和剩余 bounce 数相关,如果加入前缀路径信息效果会更好【我去,这我也想过】