(论文)[2025-SIG] Segment-based Light Transport Simulation

Posted on Edited on In Views:
论文你提出了一套新的渲染框架，基于线段（而不是传统的基于顶点）；基于这套框架，作者给出了一些采样方案和估计方案；大部分方法这样表示没啥优势，优势在于他可以实现双向的 path filtering；作者给出了实验，表明这样实现的双向 path filtering 鲁棒高效；细节不是特别明白

Segment-based Light Transport Simulation

  • Wenyou Wang、Rex West、Toshiya Hachisuka

    • 1、3：University of Waterloo, Canada
    • 2：Aoyama Gakuin University, Japan

  • 主页

  • 代码：好像只有空仓

  • 贡献

    • 新渲染框架：以 segment 作为基本元素，而不是 vertex

    • 采样框架基于 MMIS

    • 验证：实现了 robust bidirectional path filtering method

Background

  • 渲染方程
    • \(\bar{\mathrm{x}} = \{ \mathrm{x}_1, \ldots, \mathrm{x}_k \}\)

\[ I_{\rho} = \int_{\mathcal{P}} f_{\rho}(\mathrm{\bar{x}}) \,\mathrm{d}\mathrm{\bar{x}} = \sum_{k=1}^{\infty} \underbrace{\int_{\mathcal{P}_k} f_{\rho}(\mathrm{\bar{x}}) \,\mathrm{d}\mathrm{\bar{x}}}_{= I_k} \tag{1} \]

\[ f_{\rho}(\bar{\mathrm{x}}) = W_{\rho}(\mathrm{x}_1, \mathrm{x}_2) \prod_{i=1}^{k} G(\mathrm{x}_i, \mathrm{x}_{i+1}) \prod_{i=2}^{k-1} f_r(\mathrm{x}_{i-1}, \mathrm{x}_i, \mathrm{x}_{i+1}) L_e(\mathrm{x}_{k-1}, \mathrm{x}_k) \tag{2} \]

Disconnected Subpaths

  • BDPT
  • PM：收集周围光子 \(\mathrm{x}_2\) 收集 \(\mathrm{x}_2'\)，构建新光路

  • Path filtering
    • UPT 框架中，收集 kernel 内的前缀路径，连接他们的后缀路径形成新路径
    • SMIS 将 path filtering 看成一个采样过程：前缀是 technique，新路径是 sample

Paths to Segments

  • 之前的做法都是让其归约到传统 PT，采样后移除多余节点
    • VCM：kernel 内部采样【rejection sampling process】
    • SMIS：对前缀路径（technique）采样
  • UPS：连接 disconnected subpaths
    • 以 segment（节点对）为单位，light transport（根据连接概率）
    • 后续发展少（segment sampling，segment path construction）

Segment-Based Light Transport

  • 基于线段【segment】积分的框架【第一个】

Formulation

  • 积分形式

\[ J_{\rho} = \int_{\mathcal{S}} g_{\rho}(\bar{\text{s}}) \, \mathrm{d}\bar{\text{s}} = \sum_{k=1}^{\infty} \underbrace{\int_{\mathcal{S}_k} g_{\rho}(\bar{\text{s}}) \, \mathrm{d}\bar{\text{s}}}_{= J_{\rho,k}} \]

  • \(\rho\)：像素
  • \(\mathcal{S}_k=\mathcal{M}^{2k}\)：长度为 \(k\) 的线段 \(\bar{\text{s}} = \{ \text{s}_1 \ldots \text{s}_k \}\) 的集合
    • \(\text{s}_i=(\mathrm{x}_i,\mathrm{y}_i)\)
  • \(g_{\rho}(\bar{\text{s}})\) 是对像素的贡献

\[ g_{\rho}(\bar{\text{s}}) = W_{\rho}(\text{s}_1) \prod_{i=1}^{k} G(\text{s}_i) \prod_{i=1}^{k-1} K(\text{s}_i, \text{s}_{i+1}) f_r(\text{s}_i, \text{s}_{i+1}) L_e(\text{s}_k) \]

  • 相机敏感度函数 \(W_{\rho}(s) = W_{\rho}(x_1, y_1)\)
  • kernel 函数 \(K(\text{s}_i, \text{s}_{i+1})\)
  • 几何项 \(G(\text{s}_i)\)

\[ G(\text{s}_i)=\frac{|\mathrm{n}_{\text{x}_i} \cdot \bar{\text{s}}_i| \, |\mathrm{n}_{\text{y}_i} \cdot \bar{\text{s}}_i|}{|\text{x}_i - \text{y}_i|^2} V(\text{x}_i, \text{y}_i) \]

  • 自发光项 \(L_e(\text{s}_k) = L_e(\text{x}_k, \text{y}_k)\)

  • 注意
    • \(W,G,L\) 只和线段本身相关【不变的】
    • \(K,f_{r}\) 和相邻的线段相关

kernel 函数

  • \(K\) 的设计允许和方向相关，而不是简单的两个顶点
    • 可以任意给定，只需要满足能量守恒

\[ \int_{\mathcal{M}} K(\text{s}_i, \text{s}_{i+1}) \, \mathrm{d}\text{x}_{i+1} = 1 \tag{5} \]

  • 本文：有限范围内的均匀分布
    • 类似 PM，如何选择 Kernel 可以是后续工作

\[ K(\text{s}_i, \text{s}_{i+1}) = \left( \int_{\mathcal{K}(y_i)} \mathrm{d}\text{x}_{i+1} \right)^{-1} \]

  • 当 \(K\) 是 Delta 分布的时候，我们的算法退化到之前的基于顶点的表达

Throughput function

  • 为了和 Delta 时保持一致，当 \(\mathrm{x}_i=\mathrm{y}_{i+1}\) 的时候，退化为三元组

\[ f_r(\text{s}_i, \text{s}_{i+1})=f_r(\text{x}_i, \text{y}_i, \text{y}_{i+1}) \]

  • 我们提出 shift invariant【不变量】
    • \(\text{x}_{i+1}\) 依赖于 \(\text{y}_{i}\)
    • 和 path filtering 一致：不做方向修正的复用 incident radiance

\[ f_r(\text{s}_i, \text{s}_{i+1})=f_r(\text{x}_i, \text{y}_i, \text{y}_{i+1}-(\text{x}_{i+1},\text{y}_{i})) \]

  • 论文使用 shift invariant，其他作为后续工作
  • 将渲染方程展开为递归形式

\[ L(\text{s}) = L_e(\text{s}) + \int_{\mathcal{S}_1} K(\text{s}, \text{s}') f_r(\text{s}, \text{s}') G(\text{s}') L(\text{s}') \, \mathrm{d}\text{s}' \tag{7} \]

\[ J_\rho = \int_{\mathcal{S}_1} W_\rho(\text{s}) G(\text{s}) L(\text{s}) \, \mathrm{d}\text{s} \tag{8} \]

Segment Samplers and Estimators

Samplers

  • 采样示意图

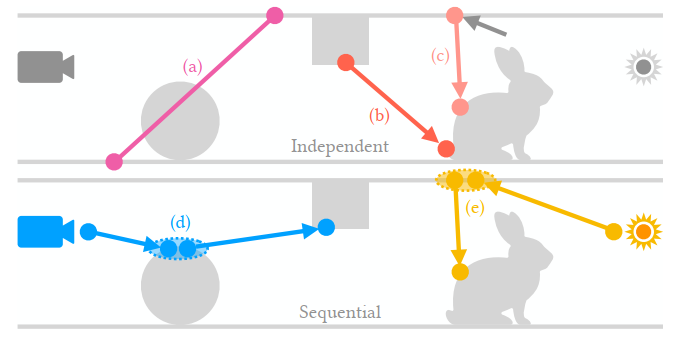
Uniform segment sampler

  • 上图的 (a)
  • 随机采样两个点，然后连起来
    • \(|\mathcal{M}|\) 表示场景面积

\[ p(\text{s}) = p(\text{x}) p(\text{y}) = \frac{1}{|\mathcal{M}|^2} \tag{12} \]

  • impractical，无重要性采样，低效

Ray tracing segment sampler

  • 稍改进一些
  • 第一个随机采，第二个点 cosine 半球采样
    • 需要从立体角转化度量为面积度量

\[ p(\text{s}) = p(\text{x}) p(\text{y} \mid \text{x}) = \frac{1}{|\mathcal{M}|} \cdot \frac{|\mathrm{n}_{\text{x}_i} \cdot \vec{\text{s}}_i| \, |\mathrm{n}_{\text{y}_i} \cdot \vec{\text{s}}_i|}{\pi |\text{x} - \text{y}|^2} = \frac{G(\text{s})}{\pi |\mathcal{M}|} \tag{13} \]

  • 结果上来说重要性采样了几何项 \(G(\text{s})\)
  • 直接重要性采样 \(\mathrm{x}\) 的BSDF：上图的 (c)
    • \(p(\bar{\text{s}} \mid \text{x}, \bar{\text{s}}')\) 正比于 BSDF，立体角度量分布

\[ p(\text{s} \mid \bar{\text{s}}') = p(\text{x}) p(\text{y} \mid \text{x}, \bar{\text{s}}') = \frac{1}{|\mathcal{M}|} \cdot \frac{p(\bar{\text{s}} \mid \text{x}, \bar{\text{s}}') \, |\mathrm{n}_{\text{y}_i} \cdot \bar{\text{s}}|}{|\text{x} - \text{y}|^2} \tag{14} \]

  • 上面方法的问题：segment 独立采样【效率低】

Sequential segment sampler

  • 类似于【path tracing、light tracing】
    • 采样一个序列【上图的 (d) (e)】
  • 初始
    • path tracing：\(p_W(\text{s}_1) \sim W_{\rho}(\text{s}_1) G(\text{s}_1)\)
    • light tracing：\(p_L(\text{s}_1) \sim L_e(\text{s}_1) G(\text{s}_1)\)
  • 后续 segment
    • 按照 kernel 采样第一个点：\(p_K(\text{x}_{i+1}\mid\text{s}_i)\sim K(\text{s}_i,\text{s}_{i+1})\)
    • 按照 BSDF 采样第二个点
$$ \[\begin{aligned} p(\text{s}_{i+1} \mid \text{s}_i) &= p(\text{x}_{i+1} \mid \text{s}_i) p(\text{y}_{i+1} \mid \text{x}_{i+1}, \text{s}_i) \\ &= p_K(\text{x}_{i+1} \mid \text{s}_i) \cdot \frac{p_\omega(\vec{\text{s}_{i+1}} \mid \text{x}_{i+1}, \text{s}_i) \, |\mathrm{n}_{\text{y}_{i+1}} \cdot \vec{\text{s}_{i+1}}|}{|\text{x}_{i+1} - \text{y}_{i+1}|^2} \end{aligned}\tag{15}\]

$$

  • virtual perturbation：复制 \(\mathrm{x}_{i+1}=\mathrm{y}_{i}\)
    • 保留 pdf \(p_K(\text{x}_{i+1}\mid\text{s}_i)\)【这样估计之后就不是无偏的了吧】
  • bridge segment：采样的线段【区别于传统的确定性连接】
    • 只是这样，没有带来好处

Estimators

  • 和 vertex 不同，segment 的采样方式不需要知道【给了更大的自由度】
  • 给一些基础算法

Sequential

  • 采样 \(k\) 个线段

\[ \langle J_{\rho k} \rangle = \frac{g_{\rho}(\bar{\text{s}})}{p(\bar{\text{s}})},\quad p(\bar{\text{s}}) = p(\text{s}_1, \ldots, \text{s}_k) \tag{16} \]

Multiple sampling techniques

  • BDPT 启发
  • \(T\) 种采样技术，每种采样技术 \(n_i\) 个样本

\[ \langle J_{\rho k} \rangle_{\text{MIS}} = \sum_{i=1}^{T} \sum_{j=1}^{n_i} \frac{w_i(\bar{\text{s}}_{i,j}) g_{\rho}(\bar{\text{s}}_{i,j})}{n_i p_i(\bar{\text{s}}_{i,j})} \tag{17} \]

  • 只需要满足对于所有路径：\(\sum_{i=1}^{T}w_i(\bar{\text{s}})=1\) 即可

Recursive estimation

\[ \langle L(\text{s}) \rangle_{\text{BH}} = L_e(\text{s}) + \sum_{i=1}^{T} \sum_{j=1}^{n_i} \frac{K(\text{s}, \text{s}_{i,j}') f_r(\text{s}, \text{s}_{i,j}') G(\text{s}_{i,j}') \langle L(\text{s}_{i,j}') \rangle_{\text{BH}}}{\sum_{i'=1}^{T} \sum_{j'=1}^{n_{i'}} p_{i'}(\text{s}_{i,j}' \mid t_{i',j'})} \tag{18} \]

  • pixel forming equation【式子 8】

\[ \langle J_{\rho} \rangle_{\text{BH}} = \sum_{i=1}^{T} \sum_{j=1}^{n_i} \frac{W_{\rho}(\text{s}_{i,j}) G(\text{s}_{i,j}) \langle L(\text{s}_{i,j}) \rangle_{\text{BH}}}{\sum_{i'=1}^{T} \sum_{j'=1}^{n_{i'}} p_{i'}(\text{s}_{i,j} \mid t_{i',j'})} \tag{19} \]

  • 直接展开有植树问题：使用 multi-vertex path filtering 高效实现
    • 类似 Path Graph / MMIS

Marginal segment path sampling

  • 不是所有的都适合递归展开
  • MMIS 对于整条路径的版本

\[ \langle J_{\rho k} \rangle_{\text{BH}} = \sum_{i=1}^{\bar{T}} \sum_{j=1}^{n_i} \frac{g_{\rho}(\bar{\text{s}}_{i,j})}{\sum_{i'=1}^{\bar{T}} \sum_{j'=1}^{n_{i'}} p_{i'}(\bar{\text{s}}_{i,j} \mid \bar{t}_{i',j'})} \tag{20} \]

Practical Algorithm

Segment-based path tracing

  • sequential segment sampler + sequential estimation
  • 避免单向的问题：BSDT + bridge segment【MIS】
  • 效果比不过 vertex-based，没有发挥 segment 的优势

Segment-based multi-vertex path filtering

  • path filtering 的 segment 版本
  • 参考 MMIS 的 path filtering
  • 相机出发：multi-vertex filtering（MVF）
  • 光源出发：photon filtering（PhF）

Bidirectional path filtering

  • 基于 vertex 的版本很难实现 bidirectional filtering【不确定？】
  • 基于线段的算法能够天然的处理来自于任意分布
  • 直接两头出发 sequential sampling，然后使用 MMIS 连接

  • 是 bidirectional photon mapping 的超集
  • kernel 的帮助下非常鲁棒

实验与讨论

  • CPU-based RGB renderer
  • 设定
    • 1200 x 800
    • segment path depth = 8
    • 1 segment path per pixel【per iteration】
    • light paths / camera paths：\(\beta=0.25\)
    • kernel 初始大小：4x average pixel footprint
      • \(\alpha=0.67\) 缩圈

Bidirectional Filtering

  • 同时间对比：MVF、PhF、BPM、UPS
    • 说是 MVF 一致的比 PT 好，所以不加 PT
    • 类似的原因不比 BDPT【但是感觉 UPS 不一定比 BDPT 好吧，而且 BDPT 后续发展还很多】
  • 复杂场景：\(\beta=1.0\)
  • 结果上来说
    • MVF、PhF【单向】存在优势场景，但是有明显的失败场景
    • BPM、UPS【双向】收敛没有我们快

其他实验

  • Filtering Efficiency and Kernel Size
    • 大 kernel 收敛快，bias 大；小 kernel 收敛慢
    • PPM 类似的缩半径策略做到了平衡
  • Path Reuse Efficiency
    • 和 BPM 相比，我们是超集；不同的 \(\beta\)
    • 我们一致的好
    • \(\beta\) 增大，MMIS 的平方计算开销导致很大的 \(\beta\) 结果反而不一定好
  • Adding Bridge Segments【具体看补充材料】
    • 同时间差；同样本好【平方计算代价高】
    • 【留给 future work】

未来工作

  • Segment sampling
    • path guiding
    • MCMC
    • 和 vertex-based sampler 结合
    • bridge segment 的重要性采样
    • 类似 BDPT 的概率链接
  • Segment paths construction
    • 泛化成 directionaless variant
  • Path filtering
    • MMIS 平方计算量
    • 如何提高 filtering efficiency
  • Temporal Filtering

补充材料

Bridge Segment Sampler

  • 最简单的策略：kernel 采样两个点，然后可见性测试连起来

\[ p(\text{s}_i \mid \text{s}_{i-1}, \text{s}_{i+1}) = p(\text{s} \mid \text{z}_{i-1}, \text{z}_{i+1}) = p_K(\text{x}_i \mid \text{z}_{i-1}) p_K(\text{y}_i \mid \text{z}_{i+1}) \tag{S6} \]

  • 类似 NEE，可以对光源（相机）采样
    • kernel 采样一个点；然后光源（相机）采样一个点

\[ p(\text{s}_i \mid \text{s}_{i-1}) = p(\text{s} \mid \text{z}_{i-1}) = p_W(\text{x}_i) p_K(\text{y}_i \mid \text{z}_{i-1}) \tag{S7} \]

\[ p(\text{s}_i \mid \text{s}_{i-1}) = p(\text{s} \mid \text{z}_{i-1}) = p_L(\text{x}_i) p_K(\text{y}_i \mid \text{z}_{i-1}) \tag{S8} \]

MMIS

  • 采样 techinque、sample 对 \((t_i,s_i)\)，然后做 MIS
  • 具体看 MMIS

实现细节

  • 核心：segment samplers、clustering algorithms、propagation
  • 每轮迭代
    • 采样线段
    • 线段顶点聚类
    • 传播线段 throughput
  • 采样线段：sequential segment samplers + bridge segment sampler
    • virtual perturbation【拷贝顶点】
    • 就是和传统的差不多
  • 聚类
    • kernel：uniform kernel
      • 定义域由 position-normal voxel encoding method 决定【spatial hashing 常用，不懂】
      • 保存所有线段端点的哈希值
      • 根据哈希值排序，实现聚类
      • 类内顶点使用相同定义域
      • 量化误差使用 jittering 转化为噪声
    • 评估 kernel 函数：计算 voxel 内部的平均位置、法向
      • 值设置为位置、法向张成平面和 voxel 的相交面积的倒数【也不太懂】
      • 这样估计会有扁案的 bias；缩 voxel 能解决
  • 传播
    • 预先计算 MMIS 权重，每一个线段最多和两个类别相关
    • 与计算完之后迭代计算，传播

  • 大概懂思路，具体细节还得看他开源代码