(论文)[2025-EGSR] Neural Path Guiding with Distribution Factorization

Posted on Edited on In Views:
neural path guiding 算法；将输出的 2D 方向拆分为两个 1D 分布的乘积；然后使用神经网络近似 1D 分布，具体上网络输出一个离散的向量，然后使用插值的方式构建 pdf（最近邻、线性）

Neural Path Guiding with Distribution Factorization

  • 作者：Pedro Figueiredo、Qihao He、Nima Khademi Kalantari
    • Texas A&M University
  • 之前的 PG 方法只占了一点【快、表达能力好】，我们试图又快又好
    • 将 2D 分布拆分为两个 1D 的条件分布【神经网络输出1D 数组作为离散分布】
    • 训练的时候，使用另外一个网络缓存 \(L_i\) 作为真值训练

Related Work

  • Global Path Guiding

    • primary sample space（PSS）
    • curse of dimensions、长路径表现差
    • 偏镜面光路算法：specular chains 那一套

  • Local Path Guiding

    • 空间、方向数据结构：kdtree、octree、vmf
    • neural
      • 近似分布参数、normalizing flow【问题在于表达能力不够】
      • 基于 CNN，甚至只能在第一跳 pg【慢】

  • Radiance Caching

  • Histogram Prediction

Method

  • 渲染方程

\[ L_o(\mathbf{x}, \omega_o) = L_e(\mathbf{x}, \omega_o) + \int_{\Omega} \rho(\mathbf{x}, \omega_o, \omega) L_i(\mathbf{x}, \omega) \lvert \cos(\theta) \rvert \,\mathrm{d}\omega \tag{1} \]

  • pg 目的
    • \(\Theta\) 表示 NN

\[ \hat{p}_{\Theta}(\omega \vert \mathbf{x}, \omega_o) \propto \rho(\mathbf{x}, \omega_o, \omega) L_i(\mathbf{x}, \omega) \vert \cos(\theta) \vert \]

  • pipeline

Distribution Factorization

  • 需求
    • 分布正比于目标分布
    • 快速采样、计算 pdf
  • 转换
    • \(\phi=2\pi\epsilon_1,\theta=\arccos(1-2\epsilon_2)\)
    • \(\hat{p}(\omega \vert \mathbf{x}, \omega_o)\) 可以转化为 \(\hat{p}(\epsilon_1, \epsilon_2 \vert \mathbf{x}, \omega_o)\)
      • 需要考虑 Jacobian 矩阵
  • 直接网络输出离散化的值【\(M_1\times M_2\)】 开销太大
  • 拆分
    • 如此只需要两个独立的网络分别输出 \(M_1\) 维的向量 \(\mathbf{v}_1\)、\(M_2\) 维的向量 \(\mathbf{v}_2\) 即可

\[ \hat{p}_{\Theta}(\epsilon_1, \epsilon_2 \vert \mathbf{x}, \omega_o) = \hat{p}_{\mathbf{w}_1}(\epsilon_1 \vert \mathbf{x}, \omega_o) \, \hat{p}_{\mathbf{w}_2}(\epsilon_2 \vert \epsilon_1, \mathbf{x}, \omega_o) \tag{3} \]

  • 如何使用离散向量：nearest neighbor、linear

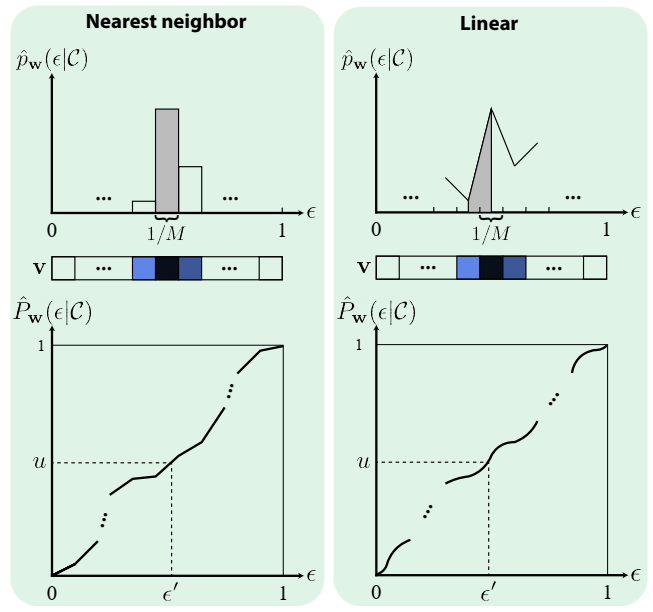
nearest neighbor

  • \(\mathcal{C}\) 是条件的简记，忽略 \(\mathbf{v}\) 的下标【二者类似】
  • pdf

\[ \hat{p}_{\mathbf{w}}(\epsilon \vert \mathcal{C}) = \mathbf{v}[\lfloor\epsilon M\rfloor] \tag{4} \]

  • cdf

\[ \hat{P}_{\mathbf{w}}(1) = \int_{0}^{1} \hat{p}_{\mathbf{w}}(\epsilon \vert \mathcal{C}) \,\mathrm{d}\epsilon = \sum_{i=0}^{M-1} \mathbf{v}[i] \frac{1}{M} = 1 \tag{5} \]

  • 需要网络输出的向量 \(\mathbf{v}\) 和为 \(M\)
    • 输出：softmax 归一化；乘上 \(M\)
  • 采样：算出 cdf，然后用它的逆

linear

  • 类似的，只不过 \(\mathbf{v}[i]\) 表示区间的中间值，然后剩余值插值【更平滑】
  • pdf

\[ \begin{align} \hat{p}_{\mathbf{w}}(\epsilon \vert \mathcal{C}) &= (1 - \alpha) \, \mathbf{v}[\lfloor m\rfloor] + \alpha \, \mathbf{v}[\lceil m\rceil] \tag{7} \\ \\ \text{where }&m = \epsilon M - 0.5,\alpha = m - \lfloor m \rfloor \tag{8} \end{align} \]

  • cdf

\[ \hat{P}_{\mathbf{w}}(1) = \int_{0}^{1} \hat{p}_{\mathbf{w}}(\epsilon \vert \mathcal{C}) \,\mathrm{d}\epsilon = \sum_{i=0}^{M-1} \frac{\mathbf{v}[i] + \mathbf{v}[i+1]}{2} \cdot \frac{1}{M} = 1 \tag{9} \]

  • 边界处理：\(\epsilon<\dfrac{1}{2M},\epsilon>1-\dfrac{1}{2M}\)
    • \(\epsilon_1\)（\(\phi\)）：对 \(\mathbf{v}_1[0],\mathbf{v}_1[M-1]\) 线性插值【\(0=2\pi\)】
    • \(\epsilon_2\)（\(\theta\)）：最近邻
  • 两种处理结果都是正确的
    • 中间部分 pdf 求和是：\(1-\dfrac{\mathbf{v}[0] + \mathbf{v}[M-1]}{2}\)
  • 采样类似

Connection to NIS

  • NIS 使用 normalizing flow 变换分布；而我们直接拆分后估计分布【离散向量】

Optimization with Radiance Caching

  • NPM 训练使用 MC 的结果，我们使用 NN 缓存 incident radiance
  • KL 散度估计【然后使用 MC 估计 KL 散度的积分】
  • 理想目标分布

\[ p(\omega_i) = \underbrace{\rho(\mathbf{x}, \omega_o, \omega_i) L_i(\mathbf{x}, \omega_i) \vert \cos(\theta_i) \vert}_{\text{integrand}} \underbrace{L_r(\mathbf{x}, \omega_o)^{-1}}_{\text{normalization factor}} \tag{13} \]

  • NPM 等实现
    • \(L_i\) 使用 MC 估计【噪声大】
    • \(L_r\) 忽略
      • 如果针对一个 \(\mathbf{x}, \omega_o\) 进行训练是 ok 的
      • 但是网络训练存在很多样本，这样会导致效果不好
  • 使用 NRC（\(f_{\Phi}\)）缓存 \(L_r\)【NRC 论文中明确说了缓存的就是 \(L_r\)，所以和本文是一样的】
  • 获取 \(L_i\)

\[ L_i(\mathbf{x}, \omega_i) = L_r(\mathbf{x}', \omega_o')=f_{\Phi}(\mathbf{x}', \omega_o') \]

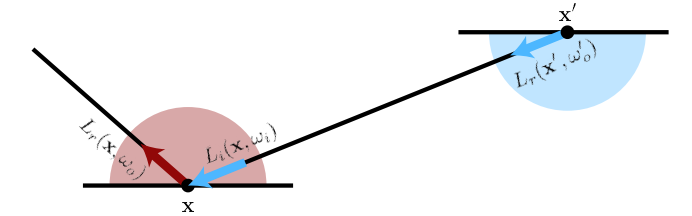
  • 同样 normalizing factor 也被解决了
  • 实验效果上缓存 \(L_r\) 的效果比 \(L_i\) 更好
    • 相当于过了一层 BSDF 的 filter
  • 理论上这只是把方差从估计 KL 散度转移到了 NRC 上
    • 但是效果确实很好
    • 得益于估计 \(L_r\)、NRC 的高效实现【relative L2 loss】
  • 和强化学习中的 actor-critic techniques 很像
    • RL：缓存 reward，从而降低优化 policy 的噪声

Implementation

  • Kiraray + TCNN
  • 30% budget 用于训练
  • 3 个网络：\(f_{\mathbf{w}_1}\)、\(f_{\mathbf{w}_2}\)、\(f_{\Phi}\)
  • 70% guiding；30% BSDF
  • \(M_1=32,M_2=16\)

Results

  • NEE off，RR off
  • max depth 6
  • RTX 3080
  • relMSE，去除 0.1% outlier，10 次取平均
  • 场景：小光源、光路难
  • 对比算法
    • PPG、Variance-Aware PG【估计 radiance】
    • NIS、NPM、我们（DF-N、DF-L）【估计 product】
      • We implement NIS with two fully-fused networks (L = 2) using piecewise quadratic coupling layers and fixed bin size and resolutions of 32 × 16 to match the capacity of our approach.
  • 等时间比较【大概都是 DF-L 最优，DF-N 次优】
    • 120s，30% 训练
    • NIS 样本数更少【说明慢但是质量高】

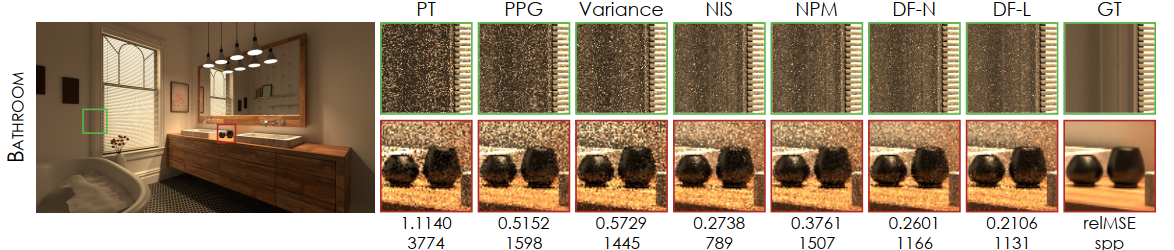
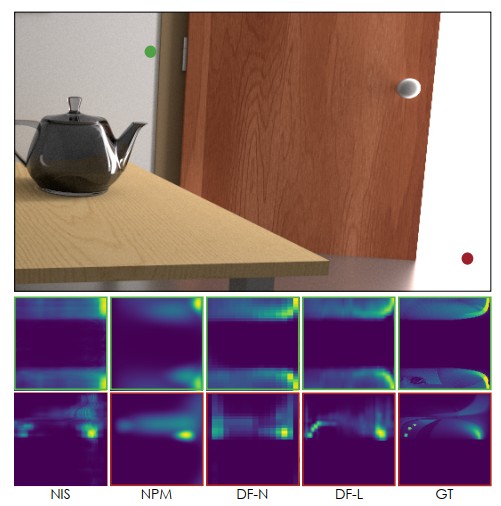
  • 上面实验的分布好坏【这个例子设计的很难，6k spp PT 还是糊的不行】
    • 只看了 product-based 的方法
    • NIS 缺失细节，因为慢导致训练样本少
    • NPM 糊了

  • 收敛性分析

Ablation

  • \(M_1,M_2\) 大小
    • trade off：开销、质量
  • caching \(L_r\)，对比
    • 式子中 \(L_i\) 用 MC 样本计算，\(L_r\) 忽略【No Cache】
    • 式子中 \(L_i\) 用 \(L_r\) 计算，\(L_r\) 忽略【\(L_i\)】
    • 式子中 \(L_i\) 用 \(L_r\) 计算，\(L_r\) 也用【\(L_i+L_r\)】

Future

  • 网络直接估计可变的 \(M_1,M_2\)
  • 局限
    • pdf 不够 sharp：游泳池场景不能很好学到光源方向，比不上 PPG 传统方法
    • 简单场景 PT、NPM 可能更好
  • Futrue：把 NN 和显式数据结构结合