(论文)[2025-EG] Neural Two-Level Monte Carlo Real-Time Rendering

Posted on Edited on In Views:
和 NRC 类似的思路，但是缓存入射辐射场 NIRC；引入双层 MC，估计 NIRC 和 GT 的残差用于保证无偏；优化了 NRC 的路径终止策略，使其能够在第一跳停止；实现做了一些优化，使其更快，能够用更多样本估计

Neural Two-Level Monte Carlo Real-Time Rendering

  • 和 NRC 类似的思路，但是缓存入射辐射场 NIRC
  • 两步 MC 算法（Two-Level Monte Carlo，subset of Multi-Level Monte Carlo，MLMC）
    • 先估计积分，然后估计残差
    • 估计积分使用 Neural Incident Radiance Cache（NIRC）
    • 估计残差使用 NIRC + PT
  • 在线学习
  • 实现上做了一些优化，推理更快

Introduction

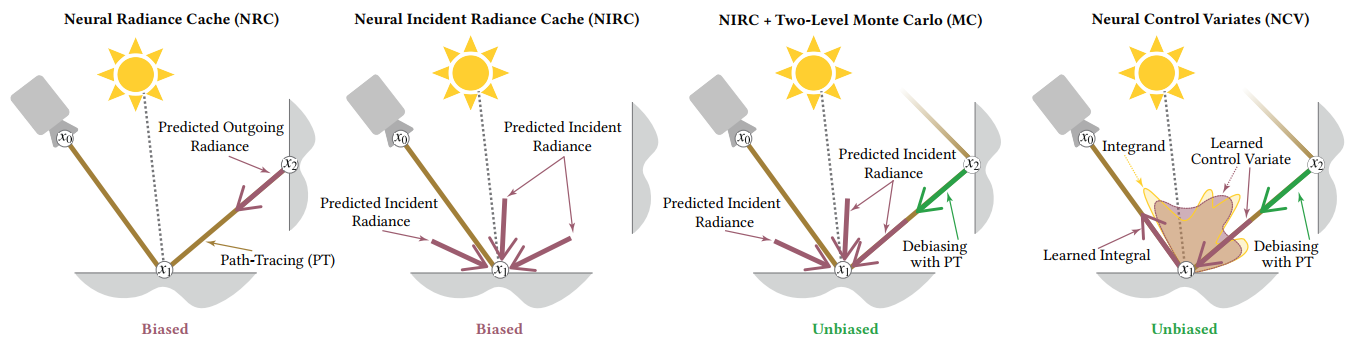
  • 一些对比
    • NIRC 直接缓存 incident radiance，比 NRC 少一次光追开销
    • biased 版本：提出了一种新的路径终止策略【Balanced Termination Heuristic（BTH）】
      • NRC 的 Spread Angle Heuristic（SPH）不能直接在第一跳使用缓存
    • 感觉确实和 CV 很像；论文中说 CV 用的一般是解析模型（SH、vMF）近似【NCV 也是近似一个分布】
  • MLMC+NIRC 在短训练时间下比 CV 效果更好
  • 比 NRC 更高效【具体看论文】
  • 环境光特殊使用，同时近似可见性

Background

  • 渲染方程、MC 求解
  • Multi-Level Monte Carlo（MLMC）
    • \(F_c\)：NIRC
      • \(\mathbf{w}\) 表示可学习的参数
    • \(F_r\)：残差的 MC 估计
    • 二者可以用不同的样本数，只要 \(F_c\) 的期望存在，那么 \(F_{tl}\) 就是无偏的

\[ F_c \approx \frac{1}{N_c} \sum_{i}^{N_c} \frac{f_c(X_i, \mathbf{w})}{p_c(X_i)} \tag{4} \]

\[ F_r \approx \frac{1}{N_r} \sum_{i}^{N_r} \frac{f(Y_i) - f_c(Y_i, \mathbf{w})}{p_r(Y_i)} \tag{5} \]

\[ F_{tl}\approx F_c+F_r \tag{6} \]

  • Control Variates（CV）
    • 形式很像，但是一般来说 \(F_c\) （期望）是数值计算得到的

Related Work

  • Radiance Caching
  • Neural Methods
  • Neural Control Variates

NIRC

  • Neural Incident Radiance Cache
  • 拆分为直接光和间接光，需要和 NEE 做 MIS
    • 这个写法感觉怪怪的？感觉不如直接写成两种策略，但是式子 9 又没有 MIS 权重

\[ L_i(x, \omega_i) = L_{ind}(x, \omega_i) + L_{nee}(x, \omega_i) \tag{8} \]

  • 间接光使用 NIRC【\(n_i\)】
    • \(\phi\) 表示辅助信息

\[ L_{ind} \approx f_c(x, \omega_i, \omega_o, \phi, \mathbf{w}) = n_i(x, \omega_i, \phi, \mathbf{w}) f_r(x, \omega_i, \omega_o) \cos\theta_i \tag{9} \]

  • 展开渲染方程
    • 有偏的就是直接不管残差项

\[ \hat{L}_o(x, \omega_o) \approx L_e(x, \omega_o) + \hat{L}_{nee}(x, \omega_o) + \hat{L}_c(x, \omega_o) + \hat{L}_r(x, \omega_o) \tag{10} \]

\[ \hat{L}_{\text{biased}}(x, \omega_o) \approx L_e(x, \omega_o) + \hat{L}_{nee}(x, \omega_o) + \hat{L}_c(x, \omega_o) \tag{13} \]

Radiance Cache Optimization

  • 损失函数两个部分
    • 残差项的方差最小化
    • 残差项的期望最小化

方差

  • 单样本方差；方差估计直接使用 MC 样本【同一个采样 pdf \(p_r\)】

\[ \left\langle \mathcal{L}_{\mathbb{V}}(f, f_c, \mathbf{w}) \right\rangle \approx \left( \frac{f(x) - f_c(x, \mathbf{w})}{p_r(x)} - F_r \right)^2 \tag{16} \]

\[ F_r = \mathbb{E} \left[ \frac{f(X) - f_c(X, \mathbf{w})}{p_r(X)} \right] \]

期望

  • 只用方差的话，biased 版本效果差

\[ \left\langle \mathcal{L}_{\text{rel}}^2(f, f_c, \mathbf{w}) \right\rangle = \frac{(f(x) - f_c(x, \mathbf{w}))^2}{p_r(x) \left( \text{sg}(f_c(x, \mathbf{w}))^2 + \epsilon \right)} \tag{18} \]

  • 原理就是让 \(\int(f(x) - f_c(x, \mathbf{w}))^2\;\mathrm{d}x\) 最小【分母是为了补偿暗区域】

Path Termination Heuristics

  • NRC

\[ \begin{align} a(x_1 \cdots x_n) &= \left( \prod_{i=2}^{n} \frac{\| x_{i-1} - x_i \|}{p(\omega_i | x_{i-1}, \omega) \cos\theta_i} \right)^2 \tag{19} \\ \\ a_0 &= \frac{\| x_0 - x_1 \|^2}{4\pi \cos\theta_1} \tag{20}\\ \\ a(x_1 \cdots x_n) &>c\cdot a_0 \tag{21} \end{align} \]

  • 扩展，使得可以在 primary hit 终止
  • 从平衡启发式得到灵感
    • NIRC glossy 处理不好，将其认为是 virtual diffuse 采样方法

\[ P_s = \frac{p(\omega_i)}{p(\omega_i) + \dfrac{N_c}{\pi}} \tag{22} \]

  • 终止条件 BTH

\[ \begin{align} i = 1: &\quad \text{stop if } \xi > P_s, \notag \\ i > 1: &\quad \text{stop if } \xi > P_s \text{ or } a(x_1 \cdots x_i) > c \cdot a_0, \tag{23} \end{align} \]

Cache Application

  • megakernel
  • 估计 \(L_c,L_r\) 的时候，使用独立的 BSDF 采样

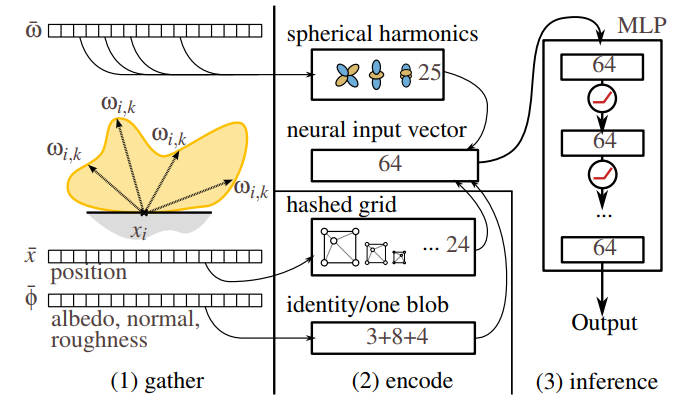
Neural Network Architecture

  • 输入：64 d
    • 位置：hash grid【12 level x 2 features】【24】
    • 方向：4 阶 SH【25】
    • albedo：identity【3】
    • normal：one-blob【8】
    • roughness：one-blob【4】

Performance Optimization

  • hash encoding 需要获取离散的位置
    • 优化：将相同的 shading surface 的 request 一起做
    • \(\phi\) 同样可以这么优化
  • SH 优化【代码开源了仔细学学】
    • full-fused，不存到 global memory，直接保存到 shared memory
    • packing + compressing 方向分量能最大化系统带宽
  • tcnn 输出的时候不使用临时 buffer【这个我也这么用了，是有优化的】
  • 优化提升：3.64x speedup【！！！】
    • sample count 表示 NIRC 样本数

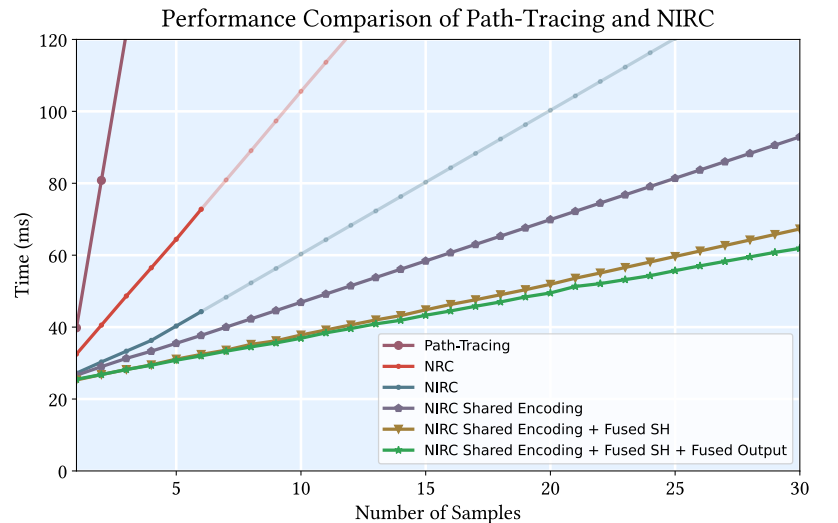
  • 训练路径、渲染路径分开 kernel
    • 训练路径长、渲染路径短【megakernel divergence 大】
    • 实现方便，而且提升了效率

Neural Visibility Cache

  • 估计环境光的可见性，0-1 实数，sigmoid 激活函数

Results

MLMC vs CV

  • 公平对比：每个像素维护自己的参数
    • 720p
    • Falcor 7 + Pytorch（TCNN bindings）
  • CV：SH、vMF【内存相当】
    • vMF：11 lobes per pixel \(\times\) 7 coeffs
      • 初始化：spherical Fibonacci lattice
      • 优化：stepwise-EM
    • SH：5 阶
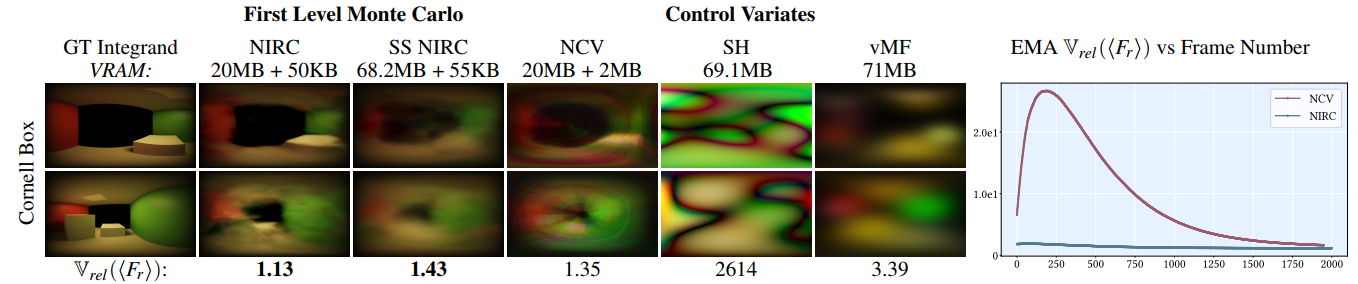
  • Screen Space NIRC（SS NIRC）
    • 输入修改为 one latent vector per pixel
    • 6 层
    • 训练帧数：4000【面向实时】
  • 学习的不仅是 incident radiance，而是整个积分【上面不是说 radiance 吗？实现上无所谓】
  • 和 NCV 对比：开源 NIS 代码【但是 NCV 本身比较也不能这么比吧，他也是优化残差的方差，下图比较合理吗？】
    • NCV 需要另外一个网络近似 BSDF
    • NCV 需要访问 MLP 18 次，NIRC 1 次
  • 同内存比较

Evaluation

  • Falcor 4.4（D3D12），TCNN（cuda）
  • NIRC
    • 4 layers 64 neurons、ReLU、Adam（lr=0.01）
    • 因为快了，所以每帧优化 4 次
  • NRC 只访问一次网络【原论文一样】
  • 训练和 NRC 相同【不使用 self-training strategy，因为效果不好】
  • 1080P，RTX3080，i7-12700k CPU 32G
  • MRSE、FLIP
  • NEE 开，light BVH
  • RR（0.1 终止）
  • 版本
    • unbiased：前 3 non-specular 跳使用预定义样本数【per-scene】访问网络，使用完整 PT 估计残差
    • biased：使用 BTH 终止 NIRC；SPH 终止 NRC【不估计残差】
      • NIRC 少光追一次，因此可以有多个样本访问网络

  • Environment map lighting：不用环境光前提下也比 NRC 好【额外实验】
  • NIRC 的样本数
    • 目前只在前 3 non-specular 跳使用 NIRC；实验没有显示出使用更多跳数的好处
    • 具体 NIRC 的样本数也是个研究话题【论文给了一些例子】
  • Memory consumption
    • surface parameter buffer：9 floats
    • encoded parameter buffer：39 half
    • encoded parameter buffer：4 bytes each direction【转化为下图的 (u,v)，估计是两个 half】
    • 前 3 跳一共 25 个样本
    • 1080P 大概 879.1 MB

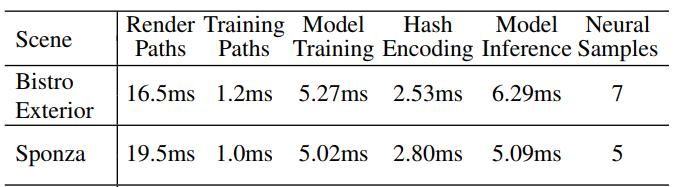
  • 大概开销分布

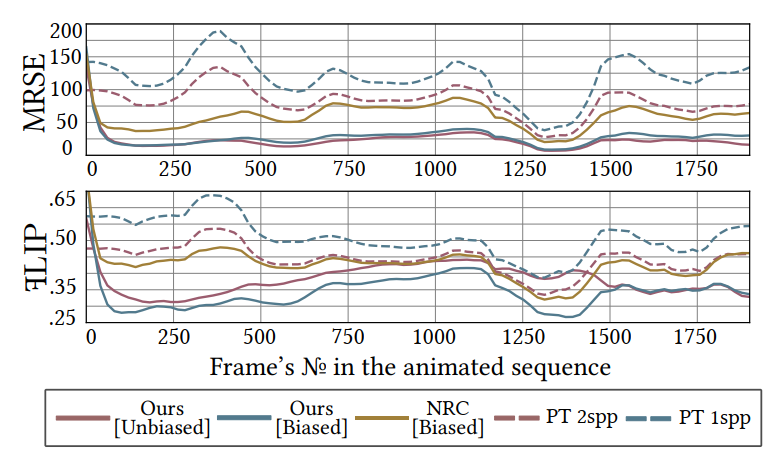
  • 动态场景支持
    • 20 帧之后就比 PT 好了【GT 1k spp】

  • Neural Visibility Cache（NVC）【这个估计的得看环境光的具体实现了】

Cache Analysis

  • NIRC vs NRC：bias，variance，path length，render time
  • 实验
    • RTX 4080，32GB RAM
    • NEE off，无环境光
    • train 2000 frames with 4 epochs

Discussion and Future Work

  • 提高 NIRC 质量【incident radiance 比较复杂】
    • 结合 NRC 和 NIRC
    • ReSTIR
  • MLMC 在哪里使用
    • MLMC 引入方差，近似的好的地方不需要用 MLMC
  • 更好适配动态场景
    • NN 陷入局部最值
  • 多层级的 MC【小的 MLP 作为低层级】
  • 残差有负值
    • 需要引入 path guiding 的时候，需要考虑这个
  • rel L2 loss 不够
    • 引入 tone mapping、perceptual loss
    • 减小梯度噪声
  • In Place Execution【内存问题】