(论文)[2022-SIG] Unbiased and consistent rendering using biased estimators

Posted on Edited on In Views:
论文提出了两种使用有偏估计构建无偏（或一致）估计的方法，分别是通过泰勒展开和伸缩和实现，给了一个通用框架；并根据这个理论实现了 3 个应用：可微渲染中的有限差分、体渲染中的 transmittance 估计、无偏光子映射

Unbiased and consistent rendering using biased estimators

  • 代码
  • 论文提出了两种使用有偏估计构建无偏（或一致）估计的方法，分别是通过泰勒展开和伸缩和实现
    • 其实重要的就是上面两个思想
  • 并根据这个理论实现了 3 个应用：可微渲染中的有限差分、体渲染中的 transmittance 估计、无偏光子映射

Introduction

  • 渲染中有很多情况都需要估计积分值
    • 虽然有很多无偏估计，但是很多时候还是得用到有偏估计
  • 假定我们有 \(I\) 的可控的有偏估计 \(\langle{I(k)}\rangle\)
    • \(k\) 可以是离散的、连续的
    • \(I(\infty)\) 不能被直接计算（复杂度太高），智能计算有限值

\[ \lim_{k\to\infty}I(k)=I\tag{1} \]

  • 将误差表示为无限和的形式
    • \(B(k):=I-I(k)\)

\[ I = I(k) + \underbrace{\sum_{j = k}^{\infty} \Delta_j}_{B(k)} \tag{2} \]

Taylor-Series Debiasing

  • 需要估计的积分可能在一个非线性函数中
    • 例如倒数，用于估计归一化因子：\(g(x)=\dfrac{1}{x}\)
    • 直接使用 MC 进行估计导致有偏
    • 在数学上这类问题被称为：期望的函数（functions of expectations）

\[ I := g(F) = g\left(\int_{\Omega} f(x) \, \mathrm{d}x\right). \tag{3} \]

  • 假定 \(f\) 有限，在 \(\alpha\) 处有收敛的泰勒展开
    • \(g^{(j)}\) 表示 \(j\) 阶微分
    • 这里使用 Taylor 的前 \(k\) 项作为有偏估计，剩余项作为偏差

\[ I := g(F) = \underbrace{\sum_{j = 0}^{k - 1} \Delta_j^{\mathrm{tay}}}_{I(k)} + \underbrace{\sum_{j = k}^{\infty} \Delta_j^{\mathrm{tay}}}_{B(k)}, \text{ with } \Delta_j^{\mathrm{tay}} = g^{(j)}(\alpha) \frac{(F - \alpha)^j}{j!}, \quad (4) \]

  • 示例如下：\(g(x)=\dfrac{1}{x}\)

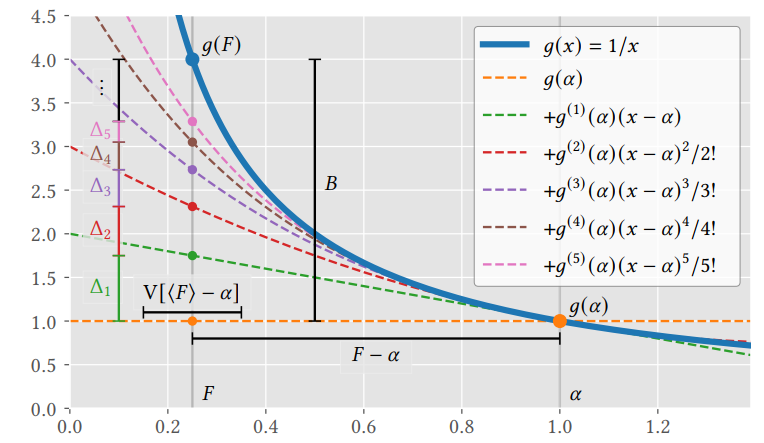
  • 泰勒展开去除了复杂的非线性项，将 \(g\) 和 \(f\) 的计算分开了
    • \((F-\alpha)^j\) 的计算可以作为 \(j\) 个独立的 \(F-\alpha\) 的乘积

之前工作

  • 形式上已经有人在图形学中用过了，但是是从其他数学形式推导过来的
    • 接下来这里讲如何转化为 Taylor 的推导形式

倒数估计

\[ g(F) := \dfrac{1}{F}\tag{5} \]

  • 令 \(k=1\)，于是有

\[ g(F) = \frac{1}{\alpha} + \sum_{j = 1}^{\infty} \Delta_j^{\mathrm{recip}}, \quad \text{where} \quad \Delta_j^{\mathrm{recip}} = \alpha^{-j - 1} (\alpha - F)^j, \tag{6} \]

  • 这里说了一些之前的应用
    • [2007] Unbiased Monte Carlo Estimation of the Reciprocal of an Integral
      • Booth
      • 最早，但不是图形学
      • 分析方式：Control Variates + Maclaurin 级数
    • [2015-TOG] Unbiased Photon Gathering for Light Transport Simulation
    • [2019-TOG] Integral Formulations of Volumetric Transmittance
    • [2020-TOG] Specular Manifold Sampling for Rendering High-Frequency Caustics and Glints
    • [2020-TOG] Path Tracing Estimators for Refractive Radiative Transfer

指数透射率估计

  • Exponential-transmittance estimation
    • 体渲染中的核心

\[ g(F) := e^{-F}\tag{7} \]

\[ F=\tau := \int_{a}^{b}\mu(x) \]

  • 令 \(k=1\)

\[ g(F) = \mathrm{e}^{-\alpha} + \sum_{j = 1}^{\infty} \Delta_j^{\mathrm{exp}}, \quad \text{where} \quad \Delta_j^{\mathrm{exp}} = \mathrm{e}^{-\alpha} \frac{(\alpha - F)^j}{j!}, \tag{8} \]

  • 如下论文都提出了等价形式，但是他们都是参考 Booth2007 的方式分析得到的
    • [2019-TOG] Integral Formulations of Volumetric Transmittance
    • [2020-TVCG] Direct Transmittance Estimation in Heterogeneous Participating Media Using Approximated Taylor Expansions
  • [2021-ARXIV] An Unbiased Ray-Marching Transmittance Estimator
    • 类似形式

Inital Value & Telescoping-Series Debiasing

  • Taylor 展开的问题（下面情况不适用）
    • 不够平滑不好展开
    • 没有收敛的泰勒展开的形式
  • 需要新的解决方案

连续形式

  • \(k\) 是连续的

  • 对 式子2 进行变形

\[ I = I(k) + B(k) = I(k) + I(\infty) - I(k)\tag{9} \]

  • 假定函数 \(I\) 的微分存在，此时转化为初值问题

\[ I = I(k) + \int_{k}^{\infty} \frac{\mathrm{d}}{\mathrm{d}x} I(x) \, \mathrm{d}x\tag{10} \]

离散形式

  • 将微分转化为单位长度积分，然后使用不定积分替代，得到式子 12

\[ I = I(k) + \sum_{j=k}^{\infty}\int_{j}^{j+1} \frac{\mathrm{d}}{\mathrm{d}x} I(x) \, \mathrm{d}x\tag{11} \]

\[ I = I(k) + \sum_{j = k}^{\infty} \Delta_j^{\mathrm{tele}}, \quad \text{where} \quad \Delta_j^{\mathrm{tele}} = I(j + 1) - I(j)\tag{12} \]

  • 此时得到伸缩和（telescoping sum）

之前工作

  • Path Tracing：将 \(k\) 看成路径长度

  • Volterra transmittance：体渲染 transmittance 计算

    • 代入 式子10
    • 我们这里通过伸缩和推导得到，原始论文通过 radiative transfer equation 推导得到（不容易扩展到 non-exponetial transmittance）

\[ I=\text{Tr}(k,b) := \exp{(-\int_{k}^{b}\mu(y)\;\mathrm{d}y)} \]

\[ \begin{align} \mathrm{Tr}(k, b) &= \mathrm{Tr}(k, k) + \int_{k}^{b} \frac{\mathrm{d}}{\mathrm{d}x} \mathrm{Tr}(x, b) \, \mathrm{d}x \\ &= 1 - \int_{k}^{b} \mu(x) \mathrm{Tr}(x, b) \, \mathrm{d}x \end{align}\tag{13} \]

  • 倒数估计

  • 图形学之外

    • 2013 Rhee 给出了式子12 的最优估计
    • 2015 Blanchet 给出了式子4 的最优估计

Estimation and Convergence

  • 构建 debiased and consistent 的估计，流程如下

Primary estimators

  • 这里说的都是离散形式，连续形式类似 式子10

  • Single-term estimator

    • 通过 \(p(j)\) 采样 \(j\)
    • \(p(j)\) 表示的是 PMF（probability mass function）
    • 证明根据定义即可

\[ \langle I \rangle_1^k = \langle I(k) \rangle + \langle B(k) \rangle = \langle I(k) \rangle + \frac{\langle \Delta_j \rangle}{p(j)}\tag{14} \]

  • Prefix-sum estimator
    • \(P(j\ge i)\) 表示的是 CMF（cumulative mass function）
    • 通过 \(p(j)\) 采样 \(j\)

\[ \langle I \rangle_1^k = \langle I(k) \rangle + \langle B(k) \rangle = \langle I(k) \rangle + \sum_{i = k}^{j} \frac{\langle \Delta_i \rangle}{P(j \geq i)}\tag{15} \]

  • 证明：考虑 \(\dfrac{\langle \Delta_i \rangle}{P(j \geq i)}\) 出现的概率
    • \(p(i)+p(i+1)\cdots\)
    • 消去分母，得证

\[ \mathbb{E}[\langle I \rangle_1^k ]=\langle I(k) \rangle +\sum_{j=k}^{\infty}p(j)\sum_{i = k}^{j} \frac{\langle \Delta_i \rangle}{P(j \geq i)} \]

Secondary Estimator

\[ \langle I \rangle_N = \frac{1}{N} \sum_{i=1}^N \langle I \rangle_1^{k_i}\tag{16} \]

  • 一般来说，设置 \(k_i=k\) 为常数就够了

  • 因为 primary estimator 是无偏的的，因此不管 \(k_i\) 为多少，结果都是无偏的

    • 例如设置为 progressive（\(k=i\)）

  • Step 1 ok

Estimation under Finite Variance

  • primary estimator 是无偏的，于是只要他的方差是有限的，那么 secondary estimator 的方差就是 \(O(1/N)\) 的（中心极限定理保证）
    • 常数项依赖于 \(\langle{\Delta_j}\rangle\) 和 \(p(j)\) 的选择
  • 试图让效率最大，等价于

\[ \underset{p(j)}{\arg \min} \, \text{Var}[\langle I \rangle_1] \, \text{C}[\langle I \rangle_1]\tag{17} \]

  • 但是这很难，更加实际的做法是最小化方差，然后再去判断是否满足 finite work-normalized variance

  • 如下选择满足方差最小，证明见附录A

    • 2013 Rhee 证明了这在离散伸缩和成立；2015 Blanchet 证明了对泰勒展开也试用

\[ p(j)\propto \sqrt{V[\langle{\Delta_j}\rangle]+\left(\Delta_j\right)^2}\tag{18} \]

  • 式子 18 更加适用，即便我们不能确切知道 \(V\left[\langle{\Delta_j}\rangle\right]\) 和 \(\Delta_(j)\)，但是我们通常可以获取到他们的渐进率（asympotric rate）
    • 然后构建 PMF
    • 接着判断 \(p(j)\) 能否归一化，能则 ok
    • 不能，判断 \(C\left[\langle{I}\rangle_1\right]\) 是否有限，有限则 ok
  • 如果上面处理都不行，则还是会导致无限方差

Estimation under Infinite Variance

  • primary 是无偏的，弱大数定律保证 secondary 依概率收敛到 \(I\)
    • 注意这里不要求 primary 的方差是有限的，但是渐进收敛率会慢于 \(O(1/N)\)
  • 此时我们可以选择构建无偏（但是方差大）的估计，或者构建一致（但是有偏）的估计

证积分例子

\[ \int_{0}^{1}\dfrac{1}{x^{\alpha}\;\mathrm{d}x} \]

  • 对于任意的 \(\alpha\in(0,1)\)，结果都是 \(\dfrac{1}{1-\alpha}\)
  • 使用均匀采样
    • \(\alpha\in(0,\dfrac{1}{2})\)：有限方差
    • \(\alpha\in[\dfrac{1}{2},1)\)：无穷方差
  • 方差分析：\(p(x)=1\)
    • 于是当前 \(\alpha\in[\dfrac{1}{2},1)\) 的时候，方差是无穷的
    • secondary 误差是 \(\text{Var}[\langle I\rangle_1]/N\)

\[ \text{Var}[\langle I\rangle_1]=\int_0^1\dfrac{1}{x^{2\alpha}}\;\mathrm{d}x-\dfrac{1}{(1-\alpha)^2} \]

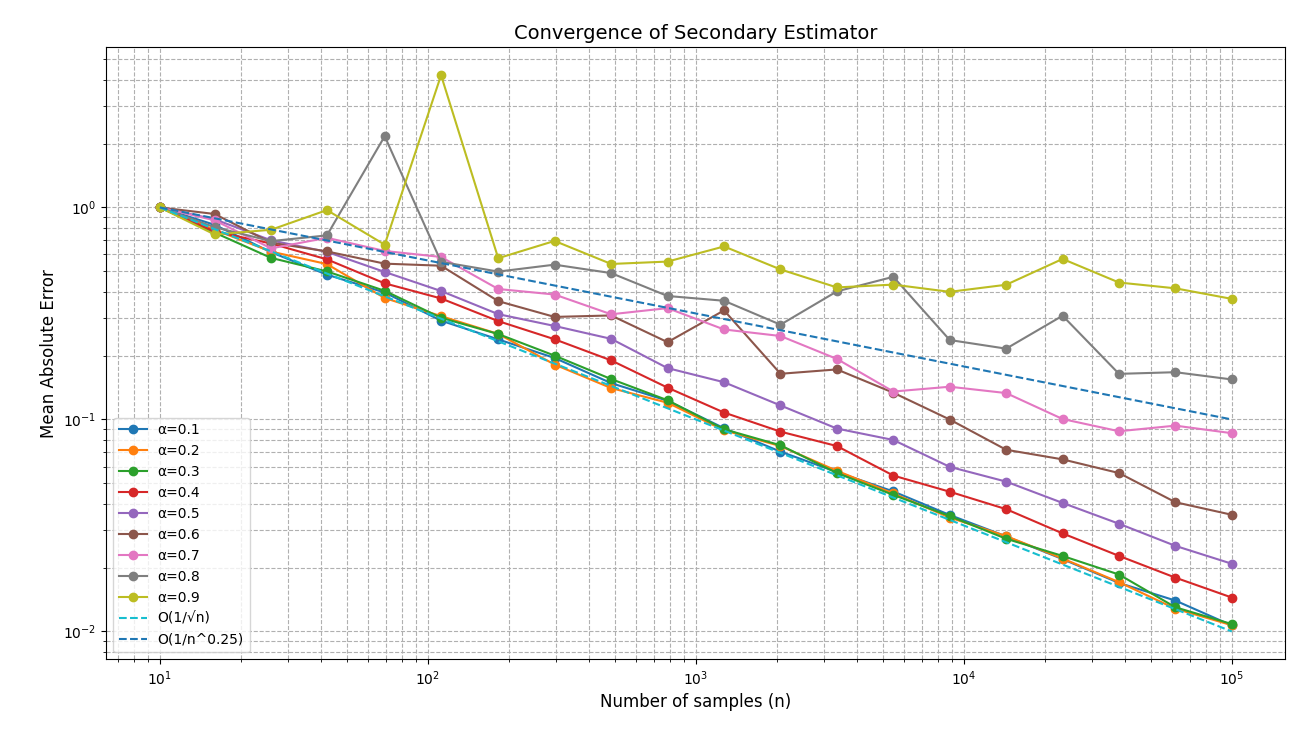
无偏估计

  • 找 \(p_j\) 让 \(\mathrm{V}\) 增长到无穷的速度尽可能慢
    • 很难找到好的策略
  • 替代方法：很多应用中 \(\mathrm{V}\) 和 \(\mathrm{C}\) 是反相关的，牺牲 \(\mathrm{C}\) 来降低 \(\mathrm{V}\)

一致估计

  • 副录 E 说明，不需要考虑 \(B(k)\) 细节，结果都是一致的
  • 思路和 PPM（progressive photon mapping）很像
  • 先构建无偏的估计，然后根据信息重参数化 \(k\)
    • 让 \(V(k_i)=\mathrm{V}[\langle I(k_i)\rangle]\) 的增长速度慢于 \(i\)（让 secondary 的方差消失）
  • 让 error 收敛率最大的 \(k\) 满足：\(O(V(k_i))=k\cdot O(B^2(k_i))\)【具体分析看副录 B】

应用

Finite differences

\[ I := \frac{\partial F(x)}{\partial x} = \frac{\partial}{\partial x} \int_{\Omega} f(x, y) \, \mathrm{d}y\tag{19} \]

  • 例如 \(f(x,y)\) 是参数 \(x\) 下路径 \(y\) 贡献【可微】
    • \(\Omega\) 可能和 \(x\) 相关
  • 有限差分在可微渲染中不实用，一般作为一个 baseline
    • 有限差分是有偏的，将其作为 GT 不太好
  • 于是我们方法有用了
  • 根据上面的方法
  • 先构建有偏估计
    • 是一致的，当 \(k\to\infty\Rightarrow h_k\to0\)
    • 我们取 \(h_k\propto2^{-k}\)
    • 定义域不同是因为可能依赖于 \(x\)

\[ \frac{\partial F(x)}{\partial x} \approx I(k) := \frac{1}{h_k} \left( \int_{\Omega_1} f(x + h_k, y_1) \, \mathrm{d}y_1 - \int_{\Omega_2} f(x, y_2) \, \mathrm{d}y_2 \right) \tag{20} \]

  • 伸缩和

\[ I = I(k) + \underbrace{\sum_{j = k}^{\infty} \Delta_j^{\mathrm{FD}}}_{B(k)}, \quad \text{where} \quad \Delta_j^{\mathrm{FD}} = I(j + 1) - I(j) \tag{21} \]

  • 使用 single-term 估计（完成 Step 1）

无偏估计

  • \(f(x,y)\) 有限，对 \(x\) 连续可微，\(\Omega\) 和 \(x\) 无关的情况下
  • 此时，理想情况下能用一个样本 \(y\) 进行估计（如下省略 \(y\)）

\[ \langle \Delta_j^{\mathrm{FD}} \rangle = \frac{\langle f(x + h_{j + 1}) \rangle - \langle f(x) \rangle}{h_{j + 1}} - \frac{\langle f(x + h_{j}) \rangle - \langle f(x) \rangle}{h_{j}}\tag{47} \]

  • \(f(x+h)\) 3阶泰勒展开，代入上式

\[ \langle \Delta_j^{\mathrm{FD}} \rangle = (h_{j + 1} - h_{j}) \left\langle \frac{\partial^2}{\partial x^2} f(x) \right\rangle + O(h_{j + 1}^2) - O(h_{j}^2) \tag{49} \]

  • 忽略高阶项，于是有

\[ \Delta_j^{\mathrm{FD}} \propto (h_{j + 1} - h_{j}), \quad \text{and} \quad \mathrm{V}[\langle \Delta_j^{\mathrm{FD}} \rangle] \propto (h_{j + 1} - h_{j})^2 \tag{50} \]

  • 用式子 18 的结论，我们得到 \(p(j)\propto 2^{-j}\)
  • 因为 cost 是常数，于是 Step 4，得到有限方差的无偏估计
  • 例子：对 roughness 的梯度估计

一致估计

  • \(f(x,y)\) 对 \(x\) 不是连续可导【例如可见性】，此时 primary 可能存在无限方差
  • Step 5 构建无偏估计，但是方差太大导致高噪声无法使用
  • Step 6 构建一致估计
  • 如果 \(\Omega\) 不依赖于 \(x\)，构造如下
    • 此时能用一个样本 \(y\) 进行估计（如下省略 \(y\)）

\[ \begin{align} \langle I(k) \rangle &= \frac{\langle f(x + h_k) - f(x) \rangle}{h_k} = \frac{1}{h_k} \int_{x}^{x + h_k} \left\langle \frac{\partial}{\partial x} f(t) \right\rangle \, \mathrm{d}t \tag{51} \\ &= \int_{-\infty}^{\infty} K(x - t) \left\langle \frac{\partial}{\partial x} f(t) \right\rangle \, \mathrm{d}t, \quad \text{where} \tag{52} \\ K(\tau) &= \begin{cases} \frac{1}{h_k} & 0 < \tau < h_k \\ 0 & \text{otherwise} \end{cases} \quad \text{is a normalized box kernel.} \tag{53} \end{align} \]

  • 效果上是 blur 了
  • 收敛慢，需要 \(h_k\to0\)

Non-exponential transmittance

  • 非指数形式计算很难，目前 raymarching（有偏）、regular tracking（慢）
  • 期望的形式，我们可以使用式子4 或者式子12 进行降噪

伸缩和

\[ \begin{aligned} &I := g(F) = \underbrace{I(k)}_{\text{biased transmittance estimate}} + \underbrace{\sum_{j = k}^{\infty} \Delta_j^{\mathrm{RM}}}_{\text{bias } B(k)},\\ &\text{with} \quad \Delta_j^{\mathrm{RM}} = I(j + 1) - I(j) \end{aligned} \tag{22} \]

  • \(I(k)\) 通过 raymarching 估计，使用单调递减序列
    • 数值方法也 ok，主要满足一致性条件
  • PMF：\(p(j)=r(1-r)^j\)【\(r=0.65\)】
  • ray marching step size \(s_j\propto 2^{-j}\)
    • 可以同时评估 \(\langle I(j+1)\rangle,\langle I(j)\rangle\)
  • 进一步减小方差
    • \(N\)个样本估计 \(\langle I(j+1)\rangle\)
    • 替换为两组 \(N/2\)个样本估计 \(\langle I(j)\rangle\) 然后平均
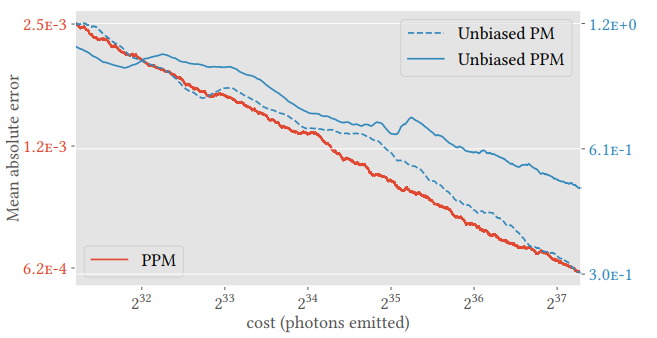
  • 实验测试，我们的算法和 regular tracking 相比是无偏的，渐近收敛率 \(O(1/N)\)
    • 测试了指数模型和 Davis and Mineev-Weinstein 模型

\[ g(F) := \left(1 + F^{\beta} C^{1 + \beta}\right)^{-\dfrac{F^{1 - \beta}}{C^{1 + \beta}}} \tag{23} \]

泰勒级数

  • Taylor series for pink-noise transmittance
  • pink noise，式子23 \(\beta=1\)

\[ g(F) := \left(1 + FC^{2}\right)^{-\dfrac{1}{C^{2}}} \tag{24} \]

  • 泰勒级数

\[ \begin{align} I := g(F) &= \underbrace{\sum_{j = 0}^{k - 1} \Delta_j^{\mathrm{pink}}}_{I(k)} + \underbrace{\sum_{j = k}^{\infty} \Delta_j^{\mathrm{pink}}}_{B(k)}, \quad \text{where} \tag{25} \\ \Delta_j^{\mathrm{pink}} &= \frac{(\alpha - F)^j}{j!} \left(1 + \alpha C^2\right)^{\frac{-1}{C^2} - j} \prod_{i = 1}^{j - 1} \left(1 + i C^2\right). \end{align} \]

  • 使用 RR 间接定义 \(p(j)\)

\[ P_{\mathrm{acc}}(j) = \frac{1 + (j - 1)C^2}{j}, \quad p(j) = (1 - P_{\mathrm{acc}}(j)) \prod_{i = 0}^{j - 1} P_{\mathrm{acc}}(i). \tag{26} \]

  • 可以使用 2021 论文中的减小方差方式
    • fixed step-size (0.2) to estimate \(\langle{F}\rangle\)
    • \(k=3\)
    • 只用 \(P=0.1\) 比例的时间估计 bias
  • 实验对比了 pink-noise，指数的 transmittance
    • 比之前方法一致的好

Photon mapping

  • 一致的：半径 \(r\to0\)
    • 存在无偏的 PM，不能处理 purely specular caustics
  • \(k\) 映射到单调递减的 \(r_k\)

\[ I = I(k) + \underbrace{\sum_{j = k}^{\infty} \Delta_j^{\mathrm{PM}}}_{B(k)}, \quad \text{where} \quad \Delta_j^{\mathrm{PM}} = I(j + 1) - I(j) \tag{27} \]

  • 已知的 PPM 理论，我们无法同时实现 Step 3&4【不能 sublinear 无偏】
  • Unbiased PM：和传统 PM 相比，噪声代替了糊
    • \(k_i=k\)
    • cone kernel
    • correlate all kernel evaluations：估计 \(\langle I(j+1)-I(j)\rangle\)，代替估计 \(\langle I(j+1)\rangle-\langle I(j)\rangle\)
      • 使用相同的样本
    • \(p(j)\propto O(j^{\alpha-2})\)，全局样本数 \(O(j^{1-c\alpha})\)【\(c=1.001,\alpha=2/3\)】
    • 半径设置【代码看的】：\(r_i=r_0\times\sqrt{(i+1)^{\alpha-1}}\)
  • Unbiased PPM
    • \(k_i=i\)
    • 和之前的 PPM 相比，多估计了 bias 这个部分
  • 收敛率分析：好像也没好，只能说 Unbiased PM 和之前的差不多

Future Work

  • 当泰勒展开和伸缩和都能用的时候，该用哪个？
    • 得看问题
  • 我们的方法能搞出更高效的倒数评估算法
  • Russian Roulette 和式子 12 是等价的
  • 我们的算法和 ADRRS 结合可能有搞头

副录

Appendix A

连续情况

  • 无偏，因此方差最小等价于二阶矩最小

\[ \mathrm{E}\left[ \left( \frac{\langle \Delta_j \rangle}{p(j)} \right)^2 \right] = \int_{k}^{\infty} \frac{\mathrm{E}\left[ \langle \Delta_x \rangle^2 \right]}{p(x)^2} p(x) \, \mathrm{d}x = \int_{k}^{\infty} \frac{\mathrm{E}\left[ \langle \Delta_x \rangle^2 \right]}{p(x)} \, \mathrm{d}x \tag{28} \]

  • 求解带约束的变分问题：Euler-Lagrange equation from the calculus of variations
    • \(\int_k^{\infty}p(x)\;\mathrm{d}x=1\)

\[ \mathcal{L}(x, \lambda, p) = \frac{\mathrm{E}\left[ \langle \Delta_x \rangle^2 \right]}{p(x)} + \lambda p(x) \tag{29} \]

  • \(\mathcal{L}\) 中不包含 \(p'\)

\[ \begin{align} \frac{\mathrm{d} \mathcal{L}}{\mathrm{d} p} - \frac{\mathrm{d}}{\mathrm{d} x} \underbrace{\left( \frac{\mathrm{d} \mathcal{L}}{\mathrm{d} p^\prime} \right)}_{=0} = 0\quad &\Leftrightarrow \quad -\frac{\mathrm{E}\left[ \langle \Delta_x \rangle^2 \right]}{p^2(x)} + \lambda = 0 \tag{30} \\ & \Leftrightarrow \quad p(x) = \sqrt{\frac{\mathrm{E}\left[ \langle \Delta_x \rangle^2 \right]}{\lambda}} \tag{31} \end{align} \]

离散形式

  • 直接使用拉格朗日乘子即可

\[ \mathrm{E}\left[ \left( \frac{\langle \Delta_j \rangle}{p(j)} \right)^2 \right] = \sum_{j = k}^{\infty} \frac{\mathrm{E}\left[ \langle \Delta_j \rangle^2 \right]}{p(j)} \tag{33} \]

\[ \mathcal{L}(\lambda, p) = \sum_{j = k}^{\infty} \frac{\mathrm{E}\left[ \langle \Delta_j \rangle^2 \right]}{p(j)} - \lambda \left( 1 - \sum_{j = k}^{\infty} p(j) \right) \tag{34} \]

\[ \begin{align} \frac{\partial \mathcal{L}}{\partial p(j)} = 0 \quad &\Leftrightarrow \quad -\frac{\mathrm{E}\left[ \langle \Delta_j \rangle^2 \right]}{p(j)^2} + \lambda = 0 \tag{35} \\ &\Leftrightarrow \quad p(j) = \sqrt{\frac{\mathrm{E}\left[ \langle \Delta_j \rangle^2 \right]}{\lambda}} \tag{36} \end{align} \]

Appendix B

  • secondary 一致性条件

\[ \lim_{N \to \infty} \text{MSE}[\langle I \rangle_N] = \lim_{N \to \infty} \left( V[\langle I \rangle_N] + B[\langle I \rangle_N]^2 \right) = 0. \tag{37} \]

  • 于是收敛条件为下面同时满足

\[ \begin{align} \lim_{N \to \infty} V[\langle I \rangle_N] &= \lim_{N \to \infty} \frac{1}{N^2} \sum_{i = 1}^{N} \underbrace{V[\langle I(k_i) \rangle]}_{V(k_i)} = \frac{O(V(k_N))}{N} = 0, \tag{38} \\ \lim_{N \to \infty} B[\langle I \rangle_N] &= \lim_{N \to \infty} \frac{1}{N} \sum_{i = 1}^{N} \underbrace{B[\langle I(k_i) \rangle]}_{B(k_N)} = O(B(k_N)) = 0, \tag{39} \end{align} \]

  • 一致性条件：需要 \(B(k)\) 消失，\(V(k)\) 的增长小于 \(O(N)\)
  • 满足上面两个条件的，MSE 收敛最快的条件为两项同阶

\[ O(V[\langle I \rangle_N]) = O(B[\langle I \rangle_N]^2)\Longrightarrow O(V(k_N)) = N\cdot O(B^2(k_N)) \]

Appendix C

  • 没太看懂
  • 条件
    • \(M_k\) 光子数，收集半径 \(r_k\)
    • 使用 single-term 伸缩和
    • 相关性的估计 \(\langle \Delta_j\rangle=\langle I(j+1)-I(j)\rangle\)【复用样本】
    • \(M_{j+1}\ne M_j\) 的话，忽略 unshared 光子
  • 这样能用 PPM 的理论
    • 【没看 PPM 的理论分析】

\[ \begin{align} V[\langle \Delta_j \rangle] &\propto \frac{1}{M_j} \int \left( k(r_{j + 1}, x) - k(r_j, x) \right)^2 \mathrm{d}x, \tag{40} \\ \Delta_j &\propto r_j^2, \tag{41} \end{align} \]

  • \(r_j=\sqrt{j^{\alpha-1}},\alpha\in(0,1)\) 都能实现一致估计
  • 此时

\[ \begin{align} \Delta_j &= O(j^{\alpha - 2}) \tag{42} \\ V[\langle \Delta_j \rangle] &= M_j^{-1} O(j^{-\alpha}), \quad \text{(constant kernel)} \tag{43} \\ V[\langle \Delta_j \rangle] &= M_j^{-1} O(j^{-\alpha - 1}). \quad \text{(cone kernel)} \tag{44} \end{align} \]

  • 然后最优 PMF 如下

\[ p(j) \propto \sqrt{V[\langle \Delta_j \rangle] + (\Delta_j)^2} = \sqrt{M_j^{-1} O(j^{-\alpha - 1}) + O(j^{2\alpha - 4})} \tag{45} \]

  • 代价无限：找不到合适的 \(\alpha,M_j\) 满足有限

\[ C[\langle I \rangle_1] \propto \sum_{j = 1}^{\infty} M_j \cdot p(j) \propto \sum_{j = 1}^{\infty} \sqrt{M_j O(j^{-\alpha - 1}) + M_j^2 O(j^{2\alpha - 4})} \tag{46} \]

Appendix E

  • \(k_i=i\)，于是有

\[ \begin{align} I &= \frac{1}{N} \sum_{k = 0}^{N} \left( I(k) + \sum_{j = k}^{\infty} \Delta_j \right) \tag{55} \\ &= \frac{1}{N} \sum_{k = 0}^{N} I(k) + \sum_{k = 0}^{N} \sum_{j = k}^{\infty} \frac{\Delta_j}{N}. \tag{56} \end{align} \]

  • 只需要满足 \(\Delta_{\infty}=0\)，那么就一致【(56) 的右边式子表示 bias，\(N\to\infty\) 的时候，趋向于 0】