(论文)[2002-CGVR] A Practical Introduction to Metropolis Light Transport

Posted on Edited on In Views:
MLT 原理简介与实现

A Practical Introduction to MLT

  • MLT 原理简介与实现

Metropolis Transport

  • 近似一个函数 \(f\)，\(f\) 能求值
  • 这里是 2D 例子，图片
  • 3 步走
    • 构建正比于 \(f\) 的采样分布
    • 从 \(f\) 构建直方图
    • 缩放：\(s=f_{ave}/h_{ave}\)
      • 实现上，\(f_{ave}\) 通过采样大量样本计算 \(f\) 平均值得到
      • \(h_{ave}\) 就是得到的直方图的平均值

例子

  • 平稳分布：stationary distribution
  • 细致平衡：detailed balance
  • idea：希望让 \(f\) 成为平稳分布，这样就能用其估计了
  • 转移函数：transition function \(K\)
    • 或者说是 mutation strategy
  • 转移概率：\(a(\bar{y}|\bar{x})\)
    • \(a\) 概率转移为 \(\bar{y}\)
    • \(1-a\) 概率维持为 \(\bar{x}\)

\[ a(\bar{y}|\bar{x})=\min\left\{1,\frac{f(\bar{y})T(\bar{x}|\bar{y})}{f(\bar{x})T(\bar{y}|\bar{x})}\right\} \]

  • 使用上面的转移函数，最终会收敛到平稳分布 \(f(\cdot)\) 【需要归一化】
  • 复制图片（没什么用，但是是一个好例子）
    • 转移策略简单的使用均匀转移：\(T(\bar{y}|\bar{x})=1/(W*H)\)
  • 代码见：ex2d.py，结果如下
突变次数(x分辨率) 结果图
1
8
64
128
reference
  • 我们可以看到即使是一个很差的突变策略，也能得到最终结果
  • 使用细致平衡得到平稳分布，这样的方式在极限定义上很鲁棒，即使 \(f\) 不能被计算只能被估计（\(\mathbb{E}[\hat{f}]=f\)），也能使用
    • 这是用于求解 light transport 的基础
  • 扩展到 RGB 也是 ok 的
    • \(f(x)=\text{luminance}(x)\)【理论上任何 \(\mathbb{R}^3\to\mathbb{R}\) 的函数都行，不一定是 luminance】
    • 在累加的时候记录需要对颜色做 luminance 归一化
      • 因为使用 \(f(\cdot)\) 作为平稳分布，那么得到的结果就已经是 luminance 的一个近似了
    • 代码见：ex2d_color.py，结果如下
突变次数(x分辨率) 结果图
1
8
64
128
reference

MLT using PT

  • 只需要满足 \(\mathbb{E}[X_f(i,j)=f(i,j)]\)，就能使用 MLT，于是流程和 RGB 一样的
    • python 伪代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
for _ in range(max_mutation):
    # 转移样本
    y = mutateAccordingToT(X)
    # 转移概率
    Tx2y = T(x, y)
    Ty2x = T(y, x)

    # 评估贡献
    Cy = evaluateLightPath(y)
    Fy = luminance(Cy)
    Cy /= Fy # 将 luminance 归一化到 1

    # 计算接受概率
    Axy = min(1, (Fy * Ty2x) / (Fx * Tx2y))

    # 接受样本
    if (np.random.rand() < Axy):
        x = y
        Fx = Fy
        Cx = Cy

    # 更新直方图
    histogram[x[0], x[1]] += Cx

记号

  • 表示方式：L（light）D（non-specular）S（specular）E（eye）
  • implicit light path：BSDF ray 击中光源

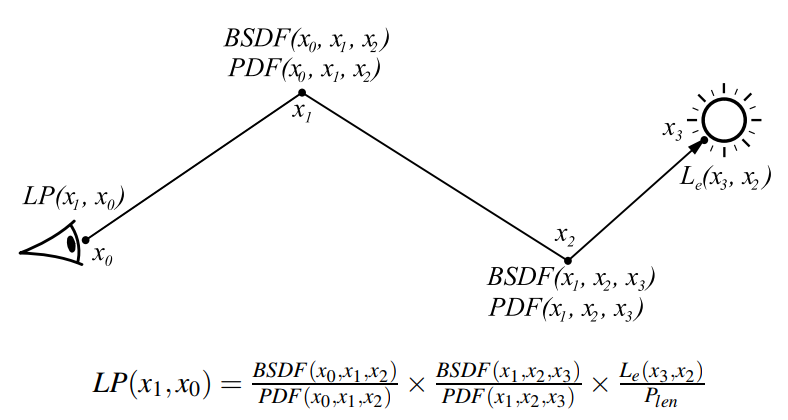
  • explicit light path：NEE 连到光源
    • \(P_{light}\)：多个光源采样到这个光源的概率
    • \(A\) 是面积
    • 面光源的话，好像多了个 \(\pi\)

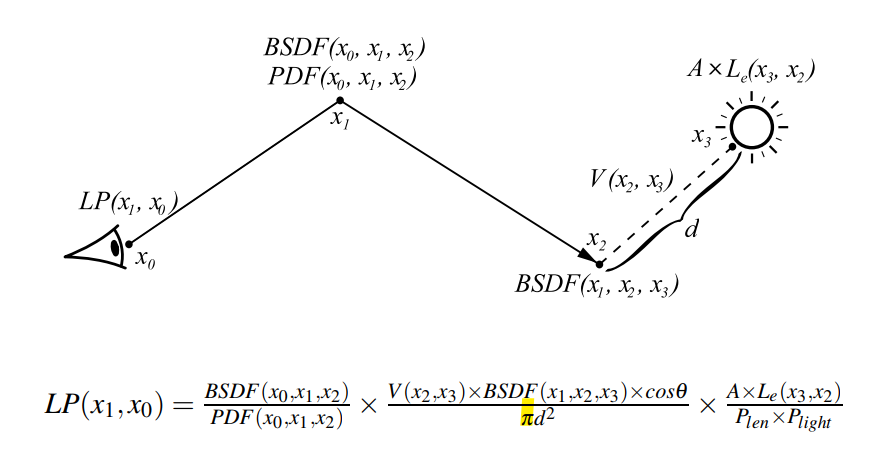
  • BSDF/PDF 计算
    • 约掉：ideal specular surface、ideal diffuse surface

A First MLT Mutation Strategy

  • 限制条件
    • \(T(\bar{x}|\bar{y})\)、\(T(\bar{y}|\bar{x})\) 的比值可以计算
    • 遍历条件：任何可能的光路径都必须可以通过一系列的变异操作从其他路径生成（不然会被困在局部）
  • new path mutation：效果不好但是满足遍历条件，通常作为变异的一部分
    • 随机选择一个像素生成随机路径，此时 \(T(\bar{x}|\bar{y})=T(\bar{y}|\bar{x})\)

Mutation and Light Path Density

  • 好的变异可能会改变采样过程，因此需要在计算 \(T(\cdot|\cdot)\) 的时候考虑
  • 一些变异规则（这里的 path density 似乎指的是最终贡献？），出射方向指 camera ray，BSDF 包括余弦项，这里都是 PT 的框架下思考问题
    • 转移概率 \(T(\bar{y}|\bar{x})\) 正比于表示从当前路径 \(\bar{x}\) 生成候选路径 \(\bar{y}\) 的概率，反比于路径 \(\bar{x}\) 的 pdf
    • 漫反射表面角度扰动，path density 变化正比于表面法线和扰动后方向的余弦
      • 出射方向改变，BSDF 变化正比于余弦，pdf 不变
    • 像素坐标的显式变化不影响 path density
    • 纯镜面多弹一下不影响 path density
    • 连接两个 diffuse 节点，path density 变化正比于 \(|\cos\theta_1\cos\theta_2/d^2|\)
      • 连接段和连接点顶点的法线
      • 类似于面光源采样对 throughput 的影响
    • 连相机，path density 变化正比于 \(|\cos\theta_2/(\cos\theta^3_1d^2)|\)
      • \(\theta_1\) 表示相机朝向和连接段的夹角
      • 类似于面光源采样，但是采样的位置不太一样，推导见最后面副录采样相机平面
        • 采样相机平面：\(\mathrm{d}x\mathrm{d}y=f^2 \sec^3 \theta_1\;\mathrm{d}\omega\)
      • 于是采样被连接的平面：\(\mathrm{d}x\mathrm{d}y=f^2 \sec^3 \theta_1\;\mathrm{d}\omega=f^2 \sec^3 \theta_1\cos\theta_2\;/d^2\mathrm{d}A\)
  • 如何理解呢？
    • MCMC 的突变会让最终的平稳分布，就是在原始 PT 采样框架下路径的贡献值（这也说明了 path density 就是最终贡献）
    • 于是我们只需要求出新路径在原始采样过程中的概率即可

Other Mutation Strategies

Mutations starting with the eye point

  • lens perturbations，multi-chain perturbations
  • 流程
    • 初始扰动：像素位置随机方向、随机大小扰动【path density 不变】
    • eye 出发，构建光路，传播相同次数的 specular bounce【path density 不变】
    • lens perturbation
      • specular 弹完之后，遇到第一个 non-specular 节点，此时将他直接连后一个节点
        • 根据规则【path density 变化 \(|\cos\theta_1\cos\theta_2/d^2|\)】
      • 例如 LDSSE 变成 LDS'S'E
        • 如果变成了 LSSE，那么不需要显式连接【path density 不变】
          • 这个能变回去吗？bounce 数都不对了，感觉是不是应该 reject
          • 可以接受，因为 mutation 保证的好像是 specular bounce 数相同，所以还能变回去
    • multi-chain perturbation
      • specular 弹完之后，遇到第一个 non-specular 节点，出射方向随机扰动【path density 变化 \(\cos\theta\)】
      • 如果接下来的顶点是 non-specular，则连回原始路径的下一个顶点，否则继续弹到和原始路径相同次数的 non-specular bounce 再连回来
      • 停止条件：原始路径用完，或者找到 non-specular 对，能连回原始路径
        • LDSSDSE => LD'S'S'D'S'E
        • 左到右分析，实际过程是右到左
          • D' non-specular 表面，连接光源 L
          • S'S' 出射方向扰动生成
          • D'S' 初始扰动生成
  • 可能会失败，一旦发生立即拒绝
    • 原始路径上的 specular 节点对应到了 non-specular
    • 没打到光源
  • 新路径的贡献值计算就和在 PT 框架中一样
  • 上面的流程主要是为了保证遍历性，否则可能变不回来
  • 计算转移函数很难，但是可以计算其比值，\(T(\bar{y}|\bar{x})\) 和 \(T(\bar{x}|\bar{y})\) 表达形式相同，但是评估方式不一样，在新路径上评估
    • \(T(\bar{y}|\bar{x})\) 在路径 \(\bar{y}\) 上评估；\(T(\bar{x}|\bar{y})\) 在路径 \(\bar{x}\) 上评估

\[ \begin{aligned} T(\bar{x}|\bar{y})=\left|\frac{d^{2}}{\cos\theta_{1}\cos\theta_{2}}\times\prod_{1\leq i\leq n}\frac{1}{\cos\phi_{i}}\right| \\ T(\bar{y}|\bar{x})=\left|\frac{d^{2}}{\cos\theta_{1}\cos\theta_{2}}\times\prod_{1\leq i\leq n}\frac{1}{\cos\phi_{i}}\right| \end{aligned}\tag{4} \]

  • 后面是扰动 diffuse，前面是主动连接

Mutations starting at the light source

  • caustic perturbation
    • **用于采样 LS*DE 路径**
  • 从光源出发扰动
  • 光源出发【或者是光源的下一个节点】，先扰动随机角度
  • 弹相同的 specular 次数，形成路径 LS*D
    • 下一个节点开始扰动则是 DS*D
    • 然后直接连 eye path【可能贡献给其他像素了】

\[ \begin{aligned} T(\bar{x}|\bar{y})=\left|\frac{1}{\cos\phi}\times\frac{d^{2}\cos^{3}\theta_{1}}{\cos\theta_{2}}\right|\\ T(\bar{y}|\bar{x})=\left|\frac{1}{\cos\phi}\times\frac{d^{2}\cos^{3}\theta_{1}}{\cos\theta_{2}}\right| \end{aligned}\tag{5} \]

  • 第一项：光源随机扰动
  • 第二项：连接相机

Estimating the Average Pixel Brightness

  • 最初始的例子，我们现在还需要估计平均亮度
  • 直接大量样本估计

BDPT

  • 追一条光子路、视子路，然后连起来（确定的）
    • 为什么不需要 MIS？

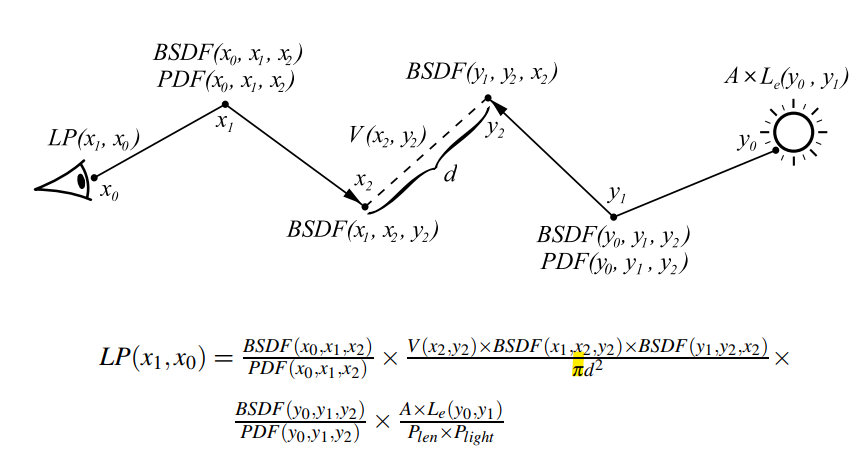
  • BDPT + MLT

副录

  • 论文最后面给了 angularOffset()、pixelOffset() mutation 的代码

采样相机平面

  • 相机焦距：\(f\)，面朝 \(z\) 轴
  • 光线方向：\(\theta_1\) 为和 \(z\) 轴夹角，\(\phi\) 是在 \(xy\) 平面上的方位角
  • 于是有，图像平面坐标 \(x,y\) 和 \(\theta_1,\phi\) 的关系如下

\[ x=f \tan \theta_1 \cos \phi, \quad y = f \tan \theta_1 \sin \phi \]

  • 求导：\(\sec\theta=1/\cos\theta\)

\[ \mathrm{d}x = f \left( \sec^2 \theta_1 \cos \phi \, d\theta_1 - \tan \theta_1 \sin \phi \, d\phi \right) \]

\[ \mathrm{d}y = f \left( \sec^2 \theta_1 \sin \phi \, d\theta_1 + \tan \theta_1 \cos \phi \, d\phi \right) \]

  • 微元面积

\[ \begin{aligned} \mathrm{d}x\mathrm{d}y &= \begin{vmatrix} x_\theta^{\prime} & x_{\phi}^{\prime} \\ y_\theta^{\prime} & y_{\phi}^{\prime} \\ \end{vmatrix} \;\mathrm{d}\theta_1\mathrm{d}\phi\\ &\\ &=\left|\frac{\partial x}{\partial \theta_1}\frac{\partial y}{\partial \phi}-\frac{\partial x}{\partial \phi}\frac{\partial y}{\partial \theta_1} \;\right|\mathrm{d}\theta_1\mathrm{d}\phi\\ &\\ &=f^2 \sec^2 \theta_1 \tan \theta_1\;\mathrm{d}\theta_1\mathrm{d}\phi \end{aligned} \]

  • 转化为立体角：\(\mathrm{d}\omega=\sin\theta_1\;\mathrm{d}\theta_1\mathrm{d}\phi\)

\[ \mathrm{d}x\mathrm{d}y=f^2 \sec^3 \theta_1\;\mathrm{d}\omega \]