(论文)[2024-SIG-C] Efficient Image-Space Shape Splatting for Monte Carlo Rendering

Posted on Edited on In Views:
论文将 splatting 和 MCMC mutation 结合，提出了一种 $O(n)$ 的 path reuse 算法；为了加速，论文在 path reuse 的时候，使用 $O(\ln n)$ 的复杂度计算贡献值，实现了进一步加速

Efficient Image-Space Shape Splatting

  • 主页
  • code
  • 论文的创新点
    • 提出了一种 path reuse 的算法，简单的复用计算 MIS 复杂度较高（balance heuristic 需要 \(O(n^2)\)，pairwise 需要 \(O(n)\) 但是效果不好），论文将splatting 和 MCMC mutation 结合，提出了一种 \(O(n)\) 的 path reuse 算法（效果好于 pairwise MIS）
      • MLT 保证了无偏性
    • 为了加速，论文在 path reuse 的时候，使用 \(O(\ln n)\) 的复杂度计算贡献值，实现了进一步加速
      • 利用了 【2022-SIG】 的方式，构建 telescope sum，将有偏转化为无偏

摘要

  • 效果
    • 屏幕空间，任意形状 shape，实现 sublinear cost 的复用
    • 能用到很多方法中（PT、PSSMLT、ReSTIR PT），单像素一致的好
  • shift mapping 计算代价是 linear 的
  • key idea：shape 内部稀疏计算随即像素的贡献，然后插值到其他像素

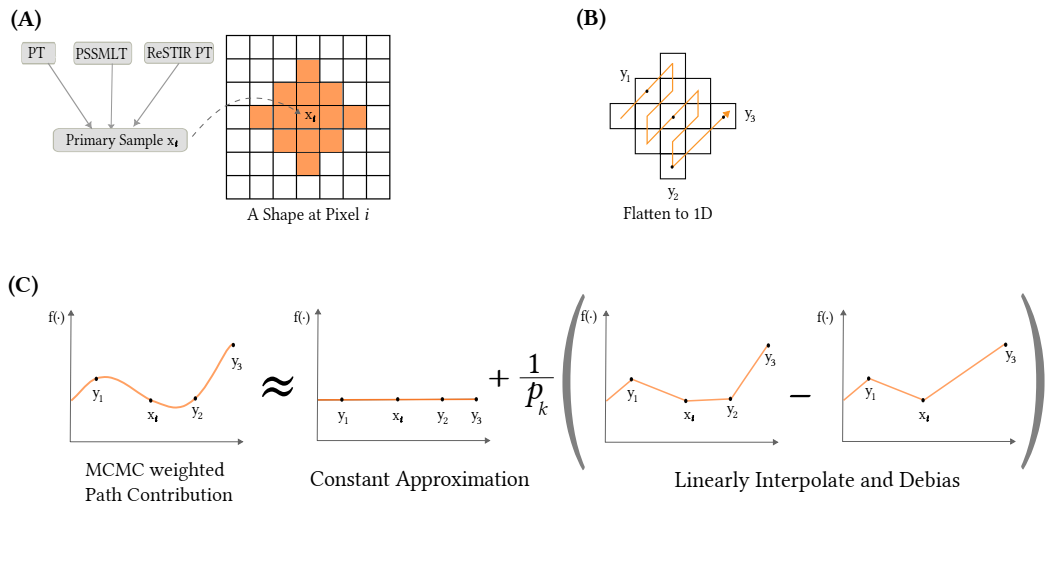
Introduction

  • 扩展 PT 概念
    • 原来是 a light path 对应 a single point
    • 扩展到 a light path 对应 multiple points，论文称为 shape
  • 自然的有 path reuse 的想法
    • 之前的 path reuse，计算复杂度正比于 shape 中 point 的数量
  • 我们：sublinear
    • 先使用 biased 快速计算 sample 对于 shape 的贡献，然后 debias
    • 结果：~60 pixel 的 shape 只需要 4 point sample
  • 使用 MCMC 来建模 shape sampling and splatting 的过程，免除平方量级的 MIS 计算

相关工作

  • Line segment sampling：之前有人做 distributed effects、visibility
  • 我们是处理由很多 point 组成的 shape，之前无人提出
  • Path reuse：ReSTIR and Generalized RIS
    • 计算代价正比于 shift mapping 的样本数
  • Gradient-domain rendering（GDR）

Motivation

  • 2D 例子
  • 问题：使用给定的 \(p(x,y)\) 去采样 \((x,y)\) 实现 拷贝图片 \(I(x,y)\)
    • 等价于估计 \(p(x,y)\) 生成样本的直方图（TODO？)
  • 使用相同的 shape，61 个点（生成代价 ~4 points）
    • 61 个点在代码中为：\(w^2+(w-1)^2,w=6\)

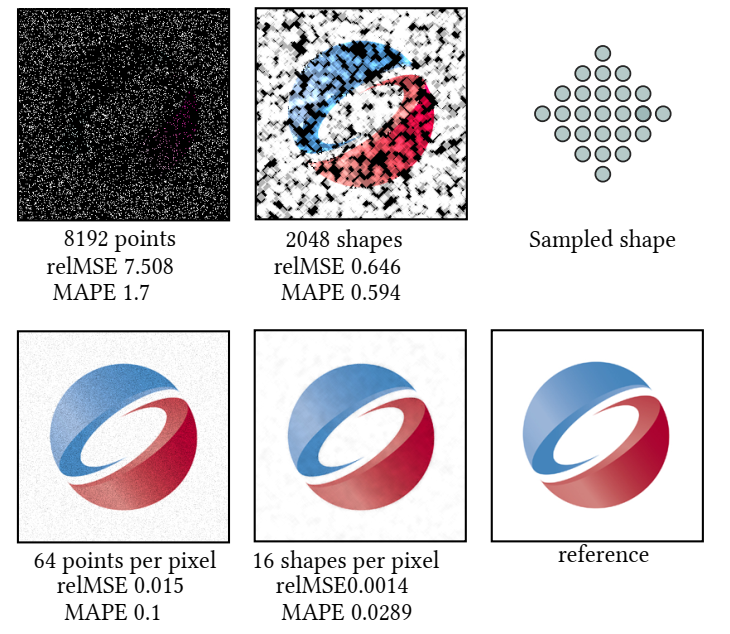
Shape Splatting

  • 积分

\[ I_i = \int_{\mathcal{P}} g(i, \mathbf{x}) d\mathbf{x} = \int_{\mathcal{P}_i} \underbrace{h(i, \mathbf{x}) f(\mathbf{x})}_{g(i,\mathbf{x})} d\mathbf{x}\tag{1} \]

  • 如果 pixel filter 为 \(h(i, \mathbf{x})=1, \mathbf{x}\in \text{pixel }i\)，向量形式如下

\[ \boldsymbol{I} = \begin{bmatrix} \vdots \\ I_i \\ \vdots \end{bmatrix} = \begin{bmatrix} \vdots \\ \int_{\mathcal{P}} g(i, \mathbf{x}) d\mathbf{x} \\ \vdots \end{bmatrix} = \begin{bmatrix} \vdots \\ \int_{\mathcal{P}_i} f(\mathbf{x}) d\mathbf{x} \\ \vdots \end{bmatrix}. \tag{2} \]

  • 流程：先根据 \(p_i(\cdot)\) 采样像素 \(i\)，然后根据 \(p(\mathbf{x}\mid i)\) 采样路径 \(\mathbf{x}\)
    • PT：等价于均匀采样 \(i\)
  • Shape：像素下标的有序集合

\[ \mathcal{S} = \{i_1, \ldots, i_{|\mathcal{S}|}\} (i_1 < \ldots < i_{|\mathcal{S}|}) \]

  • \(\mathcal{S}^i\) 用于表示不同的像素可以有不同的形状
    • \(i\) 称为 \(\mathcal{S}^i\) 的 center pixel
  • \(C(\mathcal{S}^i)_j\) ：表示形状 \(i\) 对像素 \(j\) 的贡献
  • 无偏性要求：下式是无偏估计

\[ I_j = \sum_{i = 1}^{N} C(\mathcal{S}^i)_j \]

  • \(\mathcal{S}^i\)，像素 \(i\) 的 point sample 称为 primary sample，其他的称为 secondary sample
  • naive：采样 \(\mathcal{S}^i\) 中的所有点（需要采样 n 个点，采样 shape n 次），然后将点的贡献累计到对应像素中
    • 等价于直接采样所有点，效果没有提升

Amortized Shape Splatting via Mutations

  • 复用 primary sample，用其生成所有 secondary sample
    • splatting 等价于 gathering，但是 splatting 和 MCMC mutation 更搭
  • Mutation
    • 给定 primary sample \(\mathbf{x}_i\) 和 proposal distribution \(T_i(j)\)（mutated sample 的分布）
    • 生成 secondary sample \(\{\mathbf{x}_{i_1}, \ldots, \mathbf{x}_{i_{|\mathcal{S}|}}\}\)
  • 这里我们简单的使用均匀分布
    • 因为是简单的二元分布，我们可以通过在 \(|\mathcal{S}^i|\) 个提议中恰好选择 \(\mathcal{S}^i\) 中的每个 \(j\) 一次，确定性地将主样本 \(\mathbf{x}_i\) 变换为所有其他的次样本（不懂为啥，直观好像是这样）

\[ T_i(j)=1/|\mathcal{S}^i|\cdot \mathbb{1}_{S^i}(j) \tag{4} \]

  • mutate / path reuse 方式很多，这里使用 shift mapping
  • shift mapping 生成像素 \(j\) 的样本，直接在像素 \(j\) 中生成样本；二者分布不同（假定 \(\mathcal{S}\) 都相同，那么如下）
    • \(p(\mathbf{x}\mid i) / |\partial_{\mathbf{x}} T_{i \to j}|\)
    • \(p(\mathbf{x}\mid j)\)
  • 计算 balance heuristic MIS，计算代价 \(O(|\mathcal{S^i}|^2)\)
    • pairwise MIS（\(O(|\mathcal{S^i}|)\)）
    • 我们提出替代方法【效果比 pairwise 更好】

MCMC-based Weighting for Shape Splatting

  • Metropolis-Hastings 算法
  • 状态转移的接受概率 \(a(x\to y)\)，细致平衡条件

\[ \pi(x)\mathcal{T}(x \to y)a(x \to y) = \pi(y)\mathcal{T}(y \to x)a(y \to x) \]

\[ \Longrightarrow \]

\[ a(x \to y) = \min\left(\frac{\pi(y)\mathcal{T}(y \to x)}{\pi(x)\mathcal{T}(x \to y)}, 1\right)\tag{5} \]

  • proposal distribution：\(\mathcal{T}(x \to y)\)
  • 平稳分布：\(\pi(x)\)
  • 渲染一般将当前状态和转移状态都使用
    • weighted：proposed \(y\) 权重 \(a(x\to y)\)，当前状态权重 \(1-a(x\to y)\)
    • 不会引入 bias，期望都是对的
  • \(p(\mathbf{x})\) 为初始采样光路的概率，将其作为平稳分布，于是有

\[ a(\mathbf{x}_i \to \mathbf{x}_j) = \min\left(\frac{p(\mathbf{x}_j)|\mathcal{S}^i|}{p(\mathbf{x}_i)|\mathcal{S}^j|}|\partial_{\mathbf{x}} T_{i \to j}|, 1\right)\tag{6} \]

  • 推导：都定义到 \(\mathbf{x}_i\) 的定义域上，类比推导即得

\[ \pi(\mathbf{x}_i)\mathcal{T}(\mathbf{x}_i \to \mathbf{x}_j)a(\mathbf{x}_i \to \mathbf{x}_j) = \pi(\mathbf{x}_j)\mathcal{T}(\mathbf{x}_j \to \mathbf{x}_i)a(\mathbf{x}_j \to \mathbf{x}_i) \]

\[ p(\mathbf{x}_i)\frac{1}{|\mathcal{S}^i|}a(\mathbf{x}_i \to \mathbf{x}_j) = p(\mathbf{x}_j)|\partial_{\mathbf{x}} T_{i \to j}|\frac{1}{|\mathcal{S}^j|}a(\mathbf{x}_j \to \mathbf{x}_i) \]

  • 权重计算
    • \(i=j\)：自己 + 转移其他失败

\[ w_{i \to j}= \begin{cases} \dfrac{1}{|\mathcal{S}^i|}a(\mathbf{x}_i \to \mathbf{x}_j) & (i \neq j) \\ \dfrac{1}{|\mathcal{S}^i|}\left(1 + \sum_{k \neq i} 1 - w_{i \to k}\right) & (i = j) \end{cases} \tag{7} \]

  • \(P(\mathcal{S}^i)\) 的估计

\[ \langle C(\mathcal{S}^i)\rangle_j = P(\mathcal{S}^i)_j = w_{i \to j} \frac{f(\mathbf{x}_j)}{p(\mathbf{x}_j)}, \text{ where } \mathbf{x}_j = T_{i \to j}(\mathbf{x}_i) \tag{8} \]

  • 无偏性保证
    • 我们希望 \(p(\cdot)\) 就是最终的平稳分布，代入我们的转移函数（本身就可以任意选，只会影响收敛速度），计算得到接受概率
    • 此时生成样本的概率就是 \(p(\cdot)\)，算出 pdf，除掉就行，是无偏估计

和 MCMC 的区别

  • 我们初始每个像素就有样本（根据 \(p(\cdot)\) 产生）
  • 我们设置 \(\pi(\cdot)=p(\cdot)\)，使得一开始就处于平稳分布
  • 每次多个样本（多个 secondary sample）

Efficient Shape Estimator via Debiasing

  • 目前是无偏的，但是计算量是 \(O(|\mathcal{S}^i|)\) 的
    • 需要计算每一个 secondary sample 的贡献
  • 加速：使用 telescoping sum debiasing estimators【SIG2022】
    • 具体原理看那篇论文吧
  • 这一小节：\(\mathcal{S}=\mathcal{S}^i\)，只考虑 \(j\in\mathcal{S}\)
  • \(C(\mathcal{S})\) 是一个向量
  • biased 版本： secondary sample 的 \(C(\mathcal{S})_j\approx P(\mathcal{S})_i\)
    • 称为 \(D(1)\)，因为只需要 1 个样本
  • 定义一系列估计 \(D(m)\)，使得 bias \(\mathbf{B}[D(m)]\to0\)
    • 在此，就是采样所有点，\(D(|\mathcal{S}|)=P(\mathcal{S})\)
  • \(1\le k\le |\mathcal{S}|-1\)，随机数，概率 \(p_k\)
  • 采样有序子集 \(\mathcal{K}\subset\mathcal{S}\)
    • \(\mathcal{K}\) 中有 \(k+1\) 个像素【k secondar + 1 primary】
    • 定义：\(P(\mathcal{K})_j=P(\mathcal{S})_j,j\in\mathcal{K}\)，其余为 0
    • 计算代价 \(O(|\mathcal{K}|)\)
  • 插值 \(P(\mathcal{K})\)，用于估计 \(P(\mathcal{S})\)
    • 插值操作：\(A_{\mathcal{S}}\)
    • \(A_{\mathcal{S}}(P(\mathcal{K}))=P(\mathcal{S})\)
  • telescoping sum 形式
    • \(\Delta D(k)=D(k+1)-D(k)\)
    • \(D(k)=A_{\mathcal{S}}(P(\mathcal{K}))\)

\[ P(\mathcal{S}) = D(1)+\sum_{k = 1}^{|\mathcal{S}|-1} \Delta D(k)\tag{9} \]

  • debiasing 估计
    • 容易验证，期望是无偏的

\[ \langle C(\mathcal{S})\rangle = D(1) + \frac{\Delta D(k)}{p_k} \tag{10} \]

  • 一起相关的估计 \(D(k+1),D(k)\)
    • 采样 \(k\) 个 secondary point，构建 \(\mathcal{K}\)【对应 \(D(k+1)\)】
    • 此时，遍历 \(k\) 种移除点的方式分别构建 \(D(k)\)，取均值估计

\[ \langle D(k + 1) - D(k)\rangle = \frac{1}{k}\sum_{j \in \mathcal{K}, j \neq c} A_{\mathcal{S}}(P(\mathcal{K})) - A_{\mathcal{S}}(P(\mathcal{K} - \{j\})) \tag{11} \]

  • 遗留问题：合适的 \(p_k\)
    • 2022 论文有让 \(\mathbf{V}[\langle{C(\mathcal{S})}\rangle]\) 最小的方法
    • 我们：希望让 \(\mathbf{V}[\langle{C(\mathcal{S})}\rangle]\mathbf{C}[\langle{C(\mathcal{S})}\rangle]\) 最小
      • variance x cost
  • 实验发现：\(p_k\propto k^{-2}\) 效果好
  • 期望 cost：\(\sum k p_k\to\ln k\)，实现 \(\log\) 复杂度

Efficient Interpolation Operator

  • 线性插值效果就很好
    • 超过端点的，使用最近的端点的值
  • 高阶多项式效果不好，因为插值得到的 \(C\) 可能不在 \(p(\mathcal{K})\) 的最大最小值之间（not bounded），增大方差
  • 式子 11 的计算
    • 直接计算复杂度：\(O(k|\mathcal{S}|)\)
    • 一个点的值只被两个邻居影响，加速到 \(O(|\mathcal{S}|)\)
      • 首先计算插值结果，然后根据移除的点，计算差值
      • 只需要记录每一个 \(j\) 左右各两个最近的邻居

Generalization to 2D Shapes

  • 大部分都一样，除了插值
  • 需要线性时间实现（支持 large shape）
  • 方案：1D 线性插值，沿着 space filling curve（例如 Hilbert curve）
    • 2D 沿着 curve 压成 1D

Spatially Varying Shape

  • 支持不同的像素选择不同的 shape，进一步减小式子 10 的方差
  • debias estimator 在 \(D(1)\) 和 \(P(\mathcal{S})\) 区别小的时候，效果更好
  • 利用辅助的 buffer，来实现不同的 shape
  • 实现：先分配相同的 shape \(\mathcal{S}_B\)，然后剔除其中不满足条件的像素得到 \(\mathcal{S}^i\)
    • spatially uniform base shape \(\mathcal{S}_B\)
    • 法线接近，albedo 接近
      • 无穷范数，就是最大值
      • \(\tau_n=\sqrt{2}/2,\tau_c=0.1\)

\[ n_i \cdot n_j \geq \tau_n \land \|c_i - c_j\|_{\infty} \leq \tau_c \tag{12} \]

  • 对称性保证了 secondary samples 的权重不为 0（形式化为 MCMC mutation 需要这一点）

Decorrelating Shape Splat

  • path reuse 的固有问题：inter-pixel correlation 导致的低频噪声
  • 两种方式
    • inserts strides between pixels in the shape
    • randomly rotate the shapes in each sample
  • shift mapping 导致的 error 变大，但是相关性减弱，容易被降噪（e.g. Intel OIDN）

Optional Mixing with Point Splats

  • debiasing estimator 问题
    • occasional artifacts（outlier 很难通过 auxiliary buffer 检测）
    • negative-valued pixels（差别过大）
  • 主要是在应用到 vanilla PT 中时问题明显
  • mix 3 个 estimator
    • already-available point samples at each center pixel and secondary samples（shift mapping）
    • debiasing estimator
  • 因为来自相同的样本，不能用 mis，使用 inverse variance 进行 mix
  • 可能会有些微 bias，因为方差估计依赖于样本
  • unbiased mix：future work

Results

  • 实验：MegaKernel PT、PSSMLT、ReSTIR PT
    • GPU：高效实现，解决不同 shape 导致的 divergence
      • PT 追完之后，分解小任务？
      • sample primary paths【50%开销】，dispatch resolutionSize
      • sample secondary paths【40%】，dispatch resolutionSize x nShiftedPixels
      • compute telescoping sum and splatting contribution 【10%】，dispatch resolutionSize
  • 实现了 hybrid shift mapping
  • shape size 20 ~ 80，我们算法都不错

消融实验

  • Mixing with point samples，inverse variance mix 的好处
  • Effect of debiasing，构建 telescope sum
  • Comparison between pairwise MIS and MCMC weights
    • 方差更低，outlier 更少
  • Comparison of PMFs for Debiasing
    • \(p_k=k^{-m}\)：\(1\) 方差低，但是 \(2\) 效率高
  • Debiased and naive shape splatting
    • 构建 telescope sum，引入了额外噪声；但是值得

局限

  • 如果底层渲染算法方差很大，那么效果不好，需要好的 mix 算法
  • 更好的插值算法
  • 其他应用场景，例如 PDE