(论文)[2024-SIGA] siggraph-asia 论文简介

Posted on Edited on In Views:
siggraph-asia 2024 论文

siggraph-asia-2024

(Don't) Make Some Noise: Denoising

【C】A Statistical Approach to Monte Carlo Denoising

  • 统计学降噪方法，kernel-based，考虑到传统的交叉双边滤波等方法对 GBuffer 中不存在的信息（阴影、焦散等）考虑较少，对其加上一个二值权重
  • 对于两个像素，通过最小化两个像素之间的 MSE，得到一个最优权重
  • 但是由于噪声的存在，最优权重不准，于是将其做一个二值化，而这种二值化恰好又等价于 Welch’s t-test
  • 下面式子：估计像素 \(j\) 权重，\(\rho\) 表示交叉双边滤波，\(m\) 表示二值权重

\[ w_{ij}=\dfrac{\rho_{ij}{\color{ red}m_{ij}}}{\sum_{i}\rho_{ij}{\color{ red}m_{ij}}} \]

【C】Filtering-Based Reconstruction for Gradient-Domain Rendering

  • LING-QI YAN
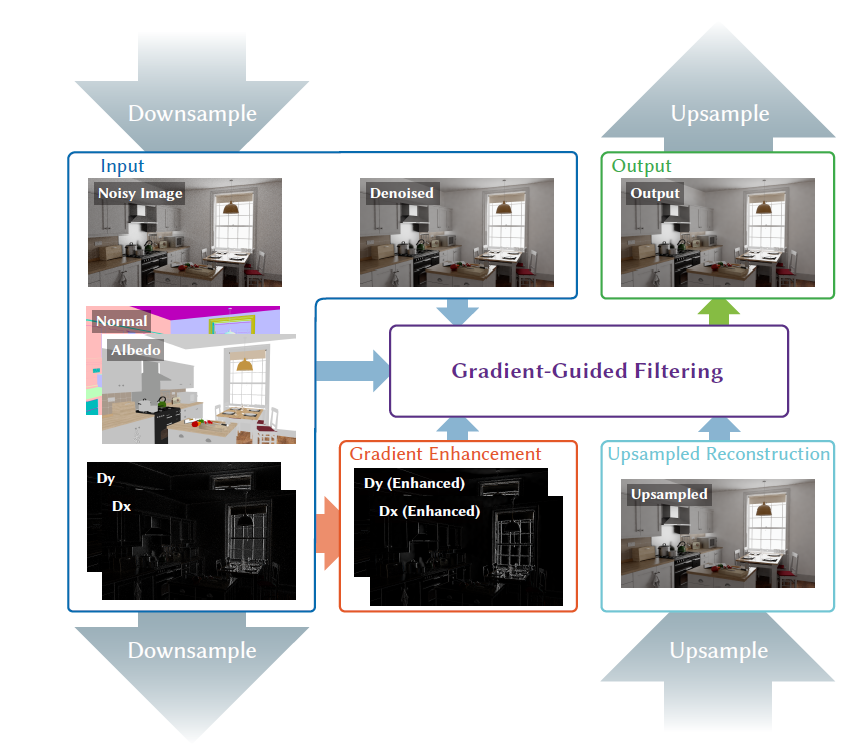
  • 简单来说就是降噪中，加入梯度信息作为指导
  • 将梯度域渲染建模成 Kernel-Based 的方法
  • 整体架构是一个金字塔架构，上下采样的权重通过 GLU【SIG-2023】的方式计算得到
  • 在每一层内，进行梯度增强、Filtering 两个操作
    • 梯度增强权重通过原始梯度图指导、GBuffer 监督得到
      • 保留梯度较大、较小的值（sharp、smooth）
      • GBuffer 变化小的地方梯度也要小
    • Filtering 的权重通过增强后的梯度、GBuffer、降噪后的图片、上采样的结果监督【优化权重系数 \(w\)】
      • MSE 小【整个流程，梯度只体现在这里的计算 \(\mu\) 真值？】
      • \(w\) 用于重建 GBuffer 也要好
      • \(w\) 重建上采样的图片应该和其本身差不多
      • \(w\) 重建后的图片更加接近降噪后的图片
  • 实验显示比之前的梯度域渲染好（收敛性好、同 spp 好），比降噪方法好（同时间好）
  • 非学习方法；渐近无偏

【C】Spatiotemporal Bilateral Gradient Filtering for Inverse Rendering

  • TZU-MAO LI，code
  • Adam 中，对输入的梯度进行降噪，对 EMA 更新的 moment 也进行降噪
  • 可微渲染中，梯度存在噪声，导致收敛慢
    • Adam 可以做时间平滑【对噪声梯度降噪；per-component 调整 lr】
      • 如果待优化的东西，各向异性很严重，则效果不好
    • inverse Laplacian operator 可以做空间平滑（over smooth）【目前基本都是各向同性】
    • 论文提出 edge-aware spatiotemporal optimizer，让效果更好【基于 cross-bilateral filter】
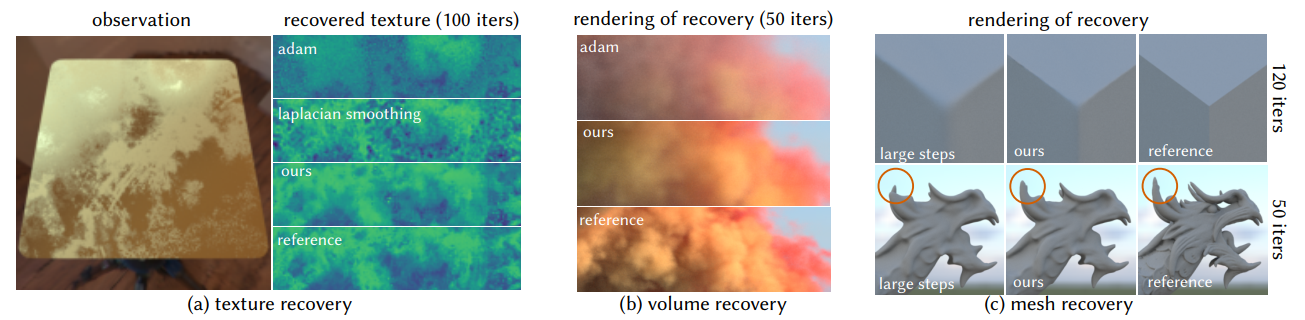
  • 应用：可微纹理、体数据、几何

  • 不需要训练
  • 之前对梯度降噪的工作：和 PT 一样设计高效的 estimator
    • 论文设计优化器

细节

  • 优化问题：\(f:\mathbb{R}^{n}\to\mathbb{R}\)，求 \(\arg\min f(\theta)\)
    • 梯度下降：\(\theta_{t+1}=\theta_t-\alpha\nabla_{\theta}f_t\)
  • CG 中的问题
    • 梯度很难算，一般是一个带噪声的估计
    • 负梯度方向不一定是最好的优化方向
      • quadratic：\(-H^{-1}\nabla_{\theta}f\)（一步优化）
      • anisotropic：\(-P^{-1}\nabla_{\theta}f\)（precondition，\(P^{-1}\) 正定）
  • Adam：temporal filtering，diagonal precondition（不考虑 \(\theta\) 各组件相关性）
    • 相关性：the pixels in an image, texels in a texture, voxels in a volume, and vertices in a mesh

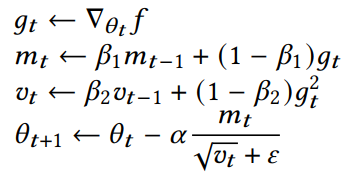
  • Anisotropic spatiotemporal filtering

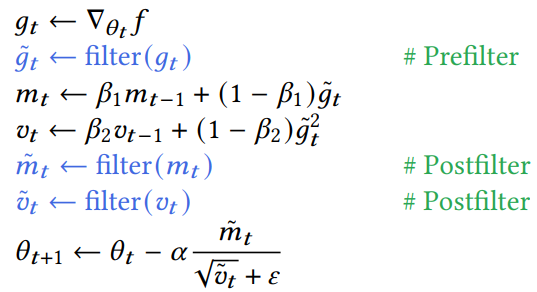
  • 不限定具体 filter，分析使用交叉双边滤波【下面是连续形式】
    • \(w_d\)：data term，保留边界
    • \(\theta\)：我们不是用参数的梯度值，而是使用参数本身【噪声更小，低动态范围，关键】
    • non-diagonal preconditioning
      • 矩阵形式：\(D^{-1}K\nabla_{\theta}f\)
        • \(K\) 考虑 \(w_s,w_d\)（对称正定仿射），建模相关性
        • \(D\)：归一化（对角）

\[ \tilde{h}(x)=\frac{1}{z(x)}\int_{\Omega}h(y)w_{s}(x,y)w_{d}(\theta(y),\theta(x))\,\mathrm{d}y \]

  • 好处：Noise removal、Non-diagonal preconditioning、Piecewise smoothness prior（分段常数）
  • Laplacian smoothing 是各向同性的特例

应用实现

  • Mitsuba 3
  • Grid-based applications
    • 实现：A-trous cross-bilateral filter（多个小的代替大的，加速）
    • texture/volume 只使用 postfiltering（收敛快）
    • Inverse texture recovery
      • a single view
      • 16spp forward，1spp gradient
      • texture：512x512
    • Inverse volume recovery
      • 64 views
      • volume：64x64x64
      • 效果：高 spp 梯度下，收敛快；低 spp 梯度下，恢复效果好
  • Inverse rendering of meshes
    • 没看，好复杂
    • 涉及到重参数化，data term 是三角形的法向

Limits

  • 我们假设参数是分段常数的
  • 超参数需要人为找

【J】Online Neural Denoising with Cross-Regression for Interactive Rendering

  • Gwangju Institute of Science and Technology, South Korea
  • 做一些 non-geometric edges （阴影等）
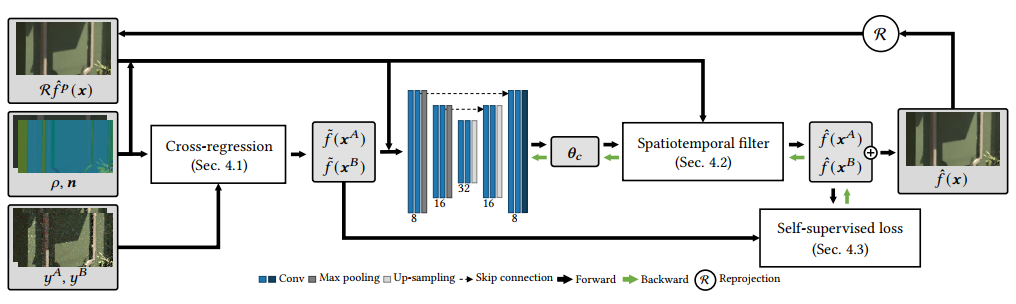
  • 在线学习（不需要真值监督），适合交互式渲染，时序稳定
  • 方法：hybrid（classical + neural）

  • Local regression：观测 \((x_i,y_i),y_i=f(x_i)+\epsilon_i\)（\(\mathbb{E}[\epsilon]=0\)），估计 \(f\)
    • 一阶展开：\(f(x_i)\approx f(x_c)+\nabla f(x_c)^{T}(x_i-x_c)\)，\(x_c\in\Omega_c\)（denoising window）
      • \(x_i,x_c\)：explanatory variables
    • 未知的 \(f(x_c),\nabla f(x_c)\) 可以使用带权重的最小二乘估计
      • weighted MSE 最小
      • 求出来之后，根据归一化的权重计算 \(f(x_i)\)
  • 论文：选择 1/16 像素求解【block-wise】
  • 问题：降噪的好坏依赖于 \(x_i,f(x_i)\) 之间的线性程度（是线性假设）
    • 之前：使用 G-buffers 作为 explanatory variables，不能保留 non-geometric edges
    • 不能获取很准确的 per-pixel MSE（样本数太少）

论文策略

  • pt 样本划分：\(y_a,y_b\)（无偏带噪）
  • 分别进行 local regression，得到 \(\tilde{f}(x^{A}),\tilde{f}(x^{B})\)，下面 A 为例子
    • GBuffer：texture \(\rho\)，normal \(n\)
    • 不一样的点：cross-regression
      • explanatory varables：\(x_i^A-x_c^A=\left[\dfrac{y_i^A-y_c^A}{\hat{\sigma}_i^A+\hat{\sigma}_i^C+\epsilon},\rho_i-\rho_c,n_i-n_c\right]^T\)
        • \(\hat{\sigma}_i^A\)：3x3 windows 内均值和像素颜色的 square distance
    • \(w_{c,i}^A=\exp\left(-\dfrac{\|y_i^A-y_c^A\|^2}{(\hat{\sigma}_i^A)^2+(\hat{\sigma}_i^C)^2+\epsilon}\right)\)
    • cross 体现：block-wise regression，使用 \(x_i^A-x_c^A,w_i^A,{\color{red}y^B}\) 计算得到 \(\tilde{f}(x^{A}_c)\)
    • 然后根据权重计算的到 \(\tilde{f}(x^{A}_i)\)，也就是 \(\tilde{f}(x^{A})\)
      • 注意这里 \(\tilde{f}(x^{A})\) 还是和 \(y^A\) 相关的（\(y^B\) 只是用于计算权重）
  • 效果还不够好，接着串一个 NN 降噪器
    • 输入：\(\tilde{f}(x^{A})\)、\(\tilde{f}(x^{B})\)、GBuffer \(\rho,n\)、上一帧重投影结果 \(\mathcal{R}\hat{f}^p(x)\)
    • 输出：\(\theta_{c}=[\theta_{c}^{A},\theta_{c}^{B},\theta_{c}^{\rho},\theta_{c}^{n},\theta_{c}^{p},\theta_{c}^{\alpha}]\)
      • \(\theta_{c}^{\alpha}\) 作为当前结果（\(\theta_{c}^{\alpha}\)）和重投影（\(1-\theta_{c}^{\alpha}\)）的插值
      • 当前结果：\(\tilde{f}(x_i^A)\) 的 cross-bilateral（其他 \(\theta^2\) 作为分母方差）
    • 最终结果：\(\tilde{f}(x_i^A),\tilde{f}(x_i^B)\) 根据权重插值
    • loss：两部分相同权重
      • \(\mathcal{L}_c^s=\dfrac{1}{2}\left(\dfrac{\|\hat{f}(x_c^A)-\tilde{f}(x_c^B)\|^2}{\|\tilde{f}(x_c^B)\|^2+\epsilon}+\cdots\right)\)
      • \(\mathcal{L}_c^t=\dfrac{1}{2}\left(\dfrac{\|\hat{f}(x_c^A)-\mathcal{R}\tilde{f}(x_c^B)\|^2}{\|\mathcal{R}\tilde{f}(x_c^B)\|^2+\epsilon}+\cdots\right)\)
    • one gradient step per frame
  • 过程中：\(y\) 进行 log-transform，最后逆变换
  • 时间：~22.26 ms（1080 P，RTX 4090）反传占一半，不算 ReSTIR PT 生成样本（~65 ms）
  • limits
    • 问题：当存在亮噪点时，会有 correlated outliers （过亮）
  • future
    • distributed effects：GBuffer 存在噪声 如何处理（pre-filtering）
    • GPU 高效实现

【J】Neural Kernel Regression for Consistent Monte Carlo Denoising

  • NN denoiser，高 spp 也能准确（收敛到 GT）

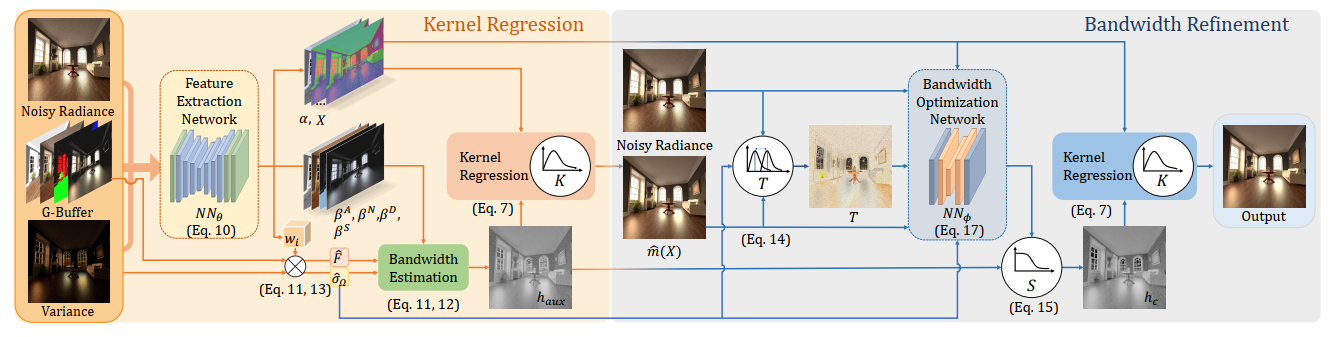
  • TODO