(论文)[2024-SIGA-C] A Statistical Approach to Monte Carlo Denoising

Posted on Edited on In Views:
统计学降噪方法，效果好于 NN，好于 sota，对于 GBuffer 中不存在的阴影、焦散等能比较好的保留；高 spp 效果才好；基于交叉双边滤波函数，在其基础上乘上一个权重系数（binary，membership function），权重系数通过最小化两点之间的 MSE 得到，计算之后通过一个阈值转化为二值函数（这个过程等价于 Welch’s t-test）

A Statistical Approach to MC Denoising

  • 项目主页
  • 作者
    • HIROYUKI SAKAI、CHRISTIAN FREUDE、THOMAS AUZINGER、DAVID HAHN、MICHAEL WIMMER
      • 3：Institute of Science and Technology Austria, Austria
      • 其他：Technische Universität Wien (TU Wien), Austria

摘要

  • 统计学方法，认为每一个像素是一个随机变量，预测其分布
  • 构建 filter 的时候，快速 pair-wise 测试，去除不合适的周围像素
  • 另外可以用在 RR、MIS
  • teaser 用的 256 spp

Introduction

  • MC denoising：bias–variance tradeoff
    • traditional image filters
      • 引入 bias（excessive blurring or color bleeding）
    • neural networks
  • 论文
    • we establish a theoretical connection between minimizing MSE for pair-wise symmetric weights and Welch’s t-test for normally distributed samples
    • 另外，应用 Box-Cox transformation 可以减小对于分布的假设
    • 在 joint bilateral filter 上实现
    • 我们可以有效避免一些模糊（例如 GBuffer 中不存在的阴影、焦散等）
    • 速度：GPU，~30 ms，720p（商用硬件）
    • 可以应用到 RR、MIS
    • 不需要训练、在线收集数据

Related Work

  • 降噪：adaptive sampling or filtering
  • Classical approaches：权衡 noise reduction、introduced bias【引入过度 blur】
    • image-filtering kernels
      • Gaussian、(joint) bilateral、non-local means（NLM）、wavelet、non-local Bayes
    • diffusion、higher-order regression
    • 和我们最接近的：带有辅助输入的交叉双边滤波
  • statistics-based approach
    • 【2012】random parameter filtering (RPF)
      • 使用特征之间的互信息调整交叉双边滤波的权重【高样本时计算开销大】
    • 【2013】稀疏计算的互信息，然后插值；试图降低计算开销，但是有限【低 spp，秒~分级别】
    • 【2014】【2017】：使用直方图表示分布；需要额外内存开销
    • 多个 filter 中挑选
      • 【2012】SURE 提高 RPF 质量
      • 【2021】
      • 【2022】Firmino，只在有利于收敛时，引入降噪
    • 我们：开销与样本数无关、ms 级别；占用内存小；不需要计算多个 denoiser
  • real-time approach
    • 【2017】需要特殊处理 DI、GI；我们更直观
  • confidence intervals
    • 之前的很复杂
  • Neural-network-based approaches
    • 需要大量训练
    • 如果特征不出现在 GBuffer 中，效果就不好（阴影、焦散）
    • 没有收敛性保证
    • 我们：不需要训练；收敛性保证；常数参数
      • 未来：automatic parameter tuning，可能提高质量

Background and Notation

  • 没一个像素的样本作为随机变量，像素 \(i\) 的 estimator 如下【GT \(\theta_i\) 未知，就是像素真值】
    • \(\hat{\theta}_i(X_1,\cdots,X_{n_i})\)
    • 假设无偏：\(\mathbb{E}[\hat{\theta}_i]=\theta_i\)
    • 称 GT 为 estimands
  • statistical tests：使用 mean（\(\mu\)）、中心矩（\(M_l,l\in[2,3,4]\)）或其变种
    • variance（\(\sigma^2=M_2\)）、skewness（\(M_3/M_2^{3/2}\)）、kurtosis（\(M_4/M_2^2\)）
    • 都可以在线计算

\[ M_l=\dfrac{1}{n_i}\sum_k(X_k-\bar{X})^l \]

Denoising Estimators

  • convex 组合得到 denoised estimator
    • 权重非负、和为1

\[ \tilde{\theta}_j=\sum_iw_{ij}\hat{\theta}_i \]

  • 我们将 \(w_{ij}\) 分为两个部分
    • base filter
    • membership function \(m_{ij}\)

\[ w_{ij}=\dfrac{\rho_{ij}m_{ij}}{\sum_{i} \rho_{ij}m_{ij}},\quad (10) \]

  • MSE=Var+Bias^2
    • Bias 是使用周围像素的时候引入的

\[ \text{MSE}(\tilde{\theta}_{j},\theta_{j})=\mathbb{E}[(\tilde{\theta}_{j}-\theta_{j})^{2}]=\text{Var}(\tilde{\theta}_{j})+\text{Bias}(\tilde{\theta}_{j},\theta_{j})^{2} \]

  • 拆解

\[ \begin{array}{c} \text{Var}(\tilde{\theta}_{j})=\sum_{i}w_{i j}^{2}\text{Var}(\hat{\theta}_{i}(n_{i}))\\ \mathrm{Bias}(\tilde{\theta}_{j},\theta_{j})=\sum_{i}w_{i j}\text{Bias}(\hat{\theta}_{i}(n_{i}),\theta_{j}) \end{array} \]

  • target

\[ \{w_{i j}^{*}\}=\operatorname*{\arg\min}_{\{w_{ij}\}}\sum_{j}\text{MSE}(\tilde{\theta}_{j},\theta_{j}),\quad(8) \]

Statistical Filtering Framework

  • 引入 membership function（\(m\)），如何组合 estimators

Problem Statement

  • 判定什么如何组合能够提高图片质量，需求如下
  • Pair-wise evaluation
    • 根据统计量评估
    • \(m_{ij}=m(\mathcal{S}(\hat{\theta}_i),\mathcal{S}(\hat{\theta}_j))\)
  • Online statistics
    • 在线更新
  • Symmetry
    • \(m_{ij}=m_{ji}\)（energy preservation）
  • Convergence
    • \(\text{Var}(\hat{\theta}_{i})\longrightarrow0\Longrightarrow m_{i j}=0\text{ if }||\theta_{i}-\theta_{j}||>0\)
    • var 为 0 时，拒绝有 bias 的估计
  • Identity
    • \(m_{ii}=1\)
    • 自身不引入 bias

Our Approach

\[ \boxed{w_{ij}=\dfrac{\rho_{ij}m_{ij}}{\sum_{i} \rho_{ij}m_{ij}}}\quad (10) \]

  • base filter \(\rho_i\)（现有的就行）
    • 限制 filter 大小，提高效率
    • 可以与现有技术结合
    • 可以使用 GBuffer 等信息
      • 实现上，我们使用 joint bilateral filter
  • 目前技术在降低方差方面效果很好，\(m_{ij}\) 的作用主要是用于限制 bias
  • 解决 MSE 最小化问题

最小化 MSE

  • 考虑一对 \(\hat{\theta}_i,\hat{\theta}_j\)
    • 降噪可以认为是一个混合

\[ \begin{array}{c} \tilde{\theta}_i=w\hat{\theta}_i+(1-w)\hat{\theta}_j\\ \tilde{\theta}_j=w\hat{\theta}_j+(1-w)\hat{\theta}_i \end{array} \]

  • 为什么是这个形式，因为我们要求对称性
    • \(w_{ij}=w_{ji}=1-w\)
    • 从下面推导上面

\[ \begin{array}{c} \tilde{\theta}_i=(1-w_{ji})\hat{\theta}_i+w_{ji}\hat{\theta}_j\\ \tilde{\theta}_j=(1-w_{ij})\hat{\theta}_j+w_{ij}\hat{\theta}_i \end{array} \]

  • Bias 如下展开

\[ \text{Bias}(\tilde{\theta}_{i},\theta_{i}) =\mathbb{E}[\tilde{\theta}_{i}-\theta_{i}] =(w-1)\theta_i+(1-w)\theta_j \]

  • 最小化 MSE（\(i,j\) 的和）

\[ \begin{array}{rl} w^{\ast}&=\arg\min_{w}\Big(\\ &w^2\text{Var}(\hat{\theta}_i)+(1-w)^2\text{Var}(\hat{\theta}_j)+((w-1)\theta_i+(1-w)\theta_j)^2\\ +&w^2\text{Var}(\hat{\theta}_j)+(1-w)^2\text{Var}(\hat{\theta}_i)+((w-1)\theta_j+(1-w)\theta_i)^2\\ &\Big) \end{array}\qquad(11) \]

  • 求偏导等于 0，算出最优的 \(w^{\ast}\)
    • 假设存在不确定性，Var+Var 不为 0

\[ w^{\ast}=\frac{2(\theta_{i}-\theta_{j})^{2}+\mathrm{Var}(\hat{\theta}_{i})+\mathrm{Var}(\hat{\theta}_{j})}{2\left((\theta_{i}-\theta_{j})^{2}+\mathrm{Var}(\hat{\theta}_{i})+\mathrm{Var}(\hat{\theta}_{j})\right)}\qquad(12) \]

  • 问题：我们不知道 GT 和 \(\text{Var}\)
    • 直接使用带噪声的值，\(m_{ij}=1-w^{\ast},\rho_{ij}=1\)，效果不好
    • 我们的选择，使用 smoothing filter \(\rho_{ij}\)，然后让 \(m_{ij}\) 作为一个二值函数

\[ m_{ij}=1 \text{ if }(1-w^{\ast})>\gamma,0\text{ otherwise} \]

  • \(\gamma\) 作为一个阈值，控制 denoising strength
    • bias 相对方差更大 => \(w^{\ast}\) 更大 => 被拒绝
    • \(1/2\Rightarrow m_{ij}=0\)
    • \(0\Rightarrow m_{ij}=1\)：退化成 base filter
  • 这个等价于 Welch’s t-test【副录】
    • \(t<\gamma_w=\sqrt{1/(2\gamma)-1}\)
  • 我们使用 Student’s t-distribution【Welch–Satterthwaite equation】【不懂，还没看】
    • \(\gamma_w=t_{1-\alpha/2},v\)
    • \(\alpha=0.005\)
    • \(v=n_i+n_j-2\)
  • Welch’s t-test 和两个正态分布的均值的置信区间相关；可以使用其他检验，放宽对正态分布的假设
  • 有很多种，可以使用高阶的统计量
    • Curto [2023] + Boc-Cox 变换，之后效果挺好的

非对称 m

  • 使用非对称的 \(m_{ij}\)，式子 11 去除 \(\arg\min\) 里面的第二项
  • 可能会导致 energy loss（过黑）
  • 其他操作和上面一样

\[ w^{\ast}_{\text{asym}}=\frac{(\theta_{i}-\theta_{j})^{2}+\mathrm{Var}(\hat{\theta}_{j})}{(\theta_{i}-\theta_{j})^{2}+\mathrm{Var}(\hat{\theta}_{i})+\mathrm{Var}(\hat{\theta}_{j})} \]

Application to Image-Space Denoising

  • 实现：pbrt-v3，cuda GPU
  • 3 个步骤
    • 在线计算统计量
    • 选择交叉双边滤波作为 \(\rho_{ij}\)
    • 实现降噪
  • MCPT 中，有些样本贡献非常高，会导致结果：right-skewed（mean > median > mode）
    • 标准正态：mean = median =mode（众数）

  • 使用 Box-Cox 变换

\[ x_{k}^{\prime}(\lambda)= \left\{\begin{array}{l l} \mathrm{log}(x_{k})&\text{if }\lambda=0\\ (x_{k}^{\lambda}-1)/\lambda&\text{otherwise} \end{array}\right. \]

  • \(\lambda=0\) 不可行，存在很多贡献为 0 的样本
  • 实验发现：\(\lambda=1/2\) 效果不错
    • 亮噪点压缩，同时暗处不会趋于过小（负）
  • 变换之后计算统计量

  • \(\rho_{ij}\)：交叉双边滤波
    • \({\bf p}_i\)：image space position, RGB albedo color, and surface normal【7D】

\[ \rho_{i j}=\exp(-\frac{1}{2}({\bf p}_j-{\bf p}_i)^{\text{T}}\Sigma^{-1}({\bf p}_j-{\bf p}_i)) \]

  • 协方差矩阵用于控制权重
    • 默认：\(\Sigma=\text{diag}\big(10,10,0.02,0.02,0.02,0.1,0.1\big)\)

  • 实现上，对每一个 RGB 通道都算 \(m_{ij}\)，只有当 3 个通道都通过测试之后，才将 \(w_{ij}\) 设置为非 0
    • 避免 color shift 问题

Results - Image Denoising

  • 测试场景输入都是高 spp 的【8192、512、256、32】

  • 收敛曲线

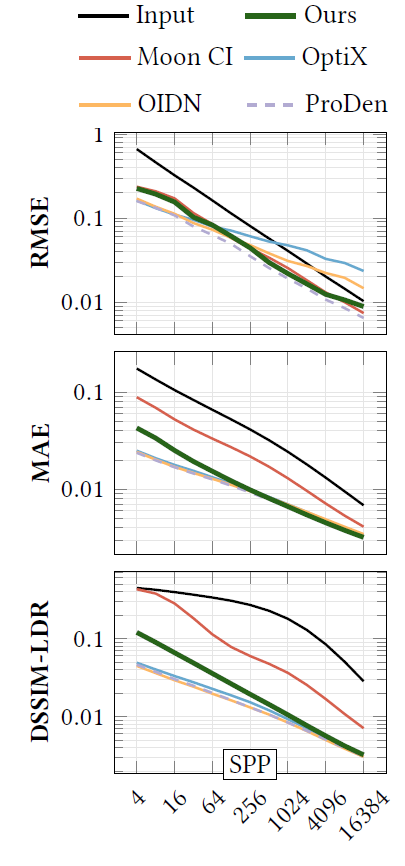
  • 网络对阴影边界处理不好（GBuffer 中没有这个信息）
  • desktop PC with an AMD Ryzen 9 5950X CPU and an NVIDIA RTX 3080 Ti GPU
  • filter size：20 pixels
  • 720p

Results - Further Applications

  • 这两个应用都太抽象了，真的会好吗？不太信

Approximate-Contribution RR

  • 怎么感觉像 ADRRS 一样，那肯定会好啊
    • 是简化版，只存储 2D 信息；像素 \(j\) 存储深度 \(d\) 的出射辐射度 \(L'_{j,k}\)【不是存储在世界空间中的，存储在 2D 图片中】
  • 对 \(L'_{j,k}\) 降噪
    • 相当于两条路径相差很大，但是他们会被平均，这样的话会非常不准，好就好在只需要保存 2D 信息
    • 降噪再使用 2D 图片，感觉非常不准，不知道为啥会好
  • 迭代法，每次迭代结束降噪；第一次迭代不开 RR

Selective MIS

  • 当有某种策略显著优于另一种策略时，MIS 可能会带来噪声
  • 我们框架：什么时候停止不好的策略？
    • 要求每一种策略都是无偏的
    • 那这个有问题啊，单独光源采样是有偏的啊（不能覆盖定义域）
  • win rate：\(\eta_m=n_m^{\ast}/n_i\)（采样策略 \(m\)）
    • \(n_m^{\ast}\)：non-zero sample，而且策略 \(m\) 的 pdf 最大
  • 对 win rate 降噪，per pixel per bounce（和上面的 RR 一样）
    • 不进行 Box-Cox transform（因为不是 radiance 了，没有 radiance 的问题）
  • 迭代法，每次迭代结束降噪
    • 第一次迭代不开 Selective MIS
    • 之后 \(\eta_m<10^{-3}\)，则停止

Discussion and Conclusion

  • 不需要预训练，不会有网络乱加细节的问题
  • Limitation
    • 低 spp 问题
  • Future
    • continuous membership functions
    • denoising variance estimates
      • 我也在想这个问题，如何对空间进行降噪呢？
    • temporal domain

副录

t-test

  • Welch’s t-test，定义如下

\[ t=\frac{\left|\hat{\theta}_{i}-\hat{\theta}_{j}\right|}{\sqrt{\sigma_{i}^{2}/n_{i}+\sigma_{j}^{2}/n_{j}}}<\gamma_{w} \]

  • 左边式子，可以得到

\[ \left(\sigma_{i}^{2}/n_{i}+\sigma_{j}^{2}/n_{j}\right)t^{2}=\left(\hat{\theta}_{i}-\hat{\theta}_{j}\right)^{2} \]

  • 式子 12 变形，\(\text{Var}(\hat{\theta}_i)=\sigma^2_i/n_i\)

\[ s=1-w^{\ast}=1-\dfrac{t^2+1/2}{t^2+1} \]

\[ t=\sqrt{\dfrac{1}{2s}-1}=\sqrt{\dfrac{1}{2(1-w^{\ast}_{ij})}-1} \]

  • 于是

\[ t<\gamma_w\Longleftrightarrow 1-w^{\ast}_{ij}>\gamma=\dfrac{1}{2(\gamma^2_w+1)} \]

加速

  • 加速点对点计算：2.5x【filter size 20 pixels】

\[ \begin{array}{c} (\hat{\theta}_{i}-\hat{\theta}_{j})^{2}<y_{w}^{2}(\sigma_{i}^{2}/n_{i}+\sigma_{j}^{2}/n_{j})\\ \hat{\theta}_{i}^{2}-\gamma_{w}^{2}\sigma_{i}^{2}/n_{i}+y_{w}^{2}\sigma_{j}^{2}/n_{j}\\ \hat{\theta}_{i}^{2}-\gamma_{w}^{2}\sigma_{i}^{2}/n_{i}<2\hat{\theta}_{i}\hat{\theta}_{j}-(\hat{\theta}_{j}^{2}-{y}_{w}^{2}\sigma_{j}^{2}/n_{j}) \end{array} \]

  • 好处：左边项、右边第二项可以预计算