(论文)[2024-SIGA-C] MARS: Multi-sample Allocation through Russian roulette and Splitting

Posted on Edited on In Views:
RRS 的 MIS 优化，不同的采样方式分配不同的光线数（EARS 是相同的）；相当于联合优化 RRS 和 MIS 分配的光线数目

MARS

  • 项目主页
  • 作者
    • JOSHUA MEYER, ALEXANDER RATH（EARS 一作）, ÖMERCAN YAZICI
      • Saarland University, Germany
    • PHILIPP SLUSALLEK, German Research Center for Artificial Intelligence, Germany and Saarland University, Germany
  • mitsuba 0.6

Introduction

  • 在之前的算法，MIS 一般都只考虑 1 sample MIS，而 RRS 工作中，对于每个 N，选择相同数量的 NEE、BSDF 光线

  • 本文优化了这点，MIS 的时候，不同策略自动选择最优的光线数

  • 示意图

      1. 只和像素有关
      1. 和像素、位置都相关

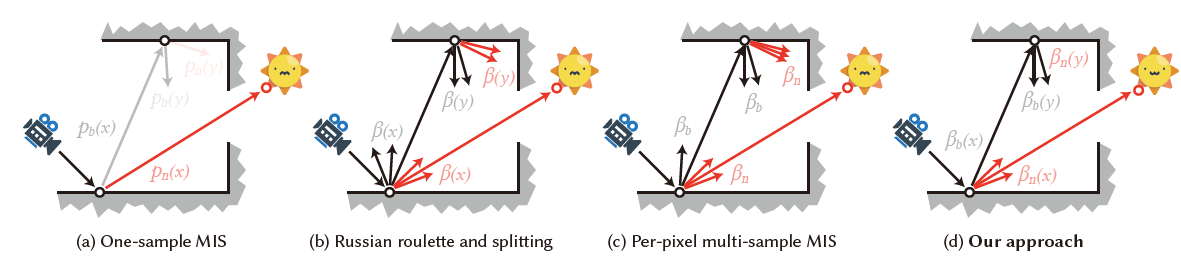
之前工作

  • Importance sampling （IS）（path guiding）
  • Multiple importance sampling（MIS）
  • Path tracing
  • Bidirectional methods：BDPT
    • 每个视子路连接相同数量的光子路
  • Mixture sampling ratios
    • 大部分只考虑直接光照，也就是说，这个 MIS weight 是 per-pixel 的【上图 (c)】
    • 只优化了：one-sample MIS
  • Russian roulette and splitting
    • BSDF rays 的数量和 NEE rays 相同
  • Multi-sample allocation
    • 简单 RRS + MIS ratio 效果不好，应该被联合优化

理论

  • 不动点迭代，EARS 的推导泛化

\[ I=\int_{\mathcal{X}}f(x)\,\mathrm{d}x \]

  • model
    • \(n_t\) 种采样策略，策略 \(t\) 分配 \(\beta_t\) 条光线（budget）
    • \(\langle I_t\rangle\)：primary estimator of technique \(t\)
    • \(\langle I;\beta\rangle\)：secondary estimator for \(I\) with \(\beta\) samples

\[ \langle I\rangle=\sum_{t=1}^{n_{t}}{\frac{1}{\beta_{t}}}\sum_{s=1}^{\beta_{t}}\langle I_{t}(x_{t,s})\rangle=\sum_{t=1}^{n_{t}}\langle I_{t}(x_{t},\cdot);\beta_{t}\rangle \]

  • 不同策略定义域可能不同（总的定义域需要包含整体），需要计算权重

\[ \langle I_{t}(x)\rangle=\sum_{i=1}^{n_{i}}{\frac{f_{i}(x)}{p_{t}(x)}}w_{i t}(x) \]

  • 连续样本数：\(\beta_t\in\mathbb{N}\to\mathbb{R}^{+}\)（好操作），最终计算光线数

\[ r(\beta)= \left\{ \begin{array}{l l} \lfloor\beta\rfloor+1&\quad\text{with probability }\beta-\lfloor\beta\rfloor,\\ \lfloor\beta\rfloor&\quad\mathrm{otherwise}\\ \end{array} \right. \]

  • 效率

\[ {\mathcal{E}}\left[\langle I\rangle\right]=\frac{1}{\mathbb{V}\left[\langle I\rangle\right]\mathbb{C}\left[\langle I\rangle\right]} \]

  • 需要考虑每一个样本 \(\beta_t\) 的 variance 和 cost

cost model

  • 每种策略的代价求和 + 汇总的代价 \(\mathbb{C}_{\Delta}\)

\[ \mathbb{C}\left[\langle I\rangle\right]=\sum_{t=1}^{n_t}\beta_t\mathbb{C}_t+\mathbb{C}_{\Delta} \]

variance model

  • 首先对所有独立采样策略求和
    • 【式子 1】

\[ \mathbb{V}\left[\langle I\rangle\right]=\sum_{t=1}^{n_t}\mathbb{V}\left[\langle I_{t};\beta_{t}\rangle\right] \]

  • 存在 stochastic rounding（小数部分）【先不管，副录有证明】
    • \(\langle I_t\rangle\) 表示只用这种技术（的方差、期望）

\[ \mathbb{V}\left[\langle I_{t};\beta_{t}\rangle\right] = \frac{1}{\beta_{t}}\mathbb{V}\left[\langle I_{t}\rangle\right] + \rho(\beta_{t})\mathbb{E}^{2}\left[\langle I_{t}\rangle\right] \]

\[ \rho(\beta)=\dfrac{(\beta-\lfloor\beta\rfloor)(\lceil\beta\rceil-\beta)}{\beta^2} \]

优化

  • 找到最优的 \(\beta_t\)，让 \({\mathcal{E}}^{-1}\left[\langle I\rangle\right]\) 最小
  • 方差计算
    • 推导
    • 但是由于 \(\beta_t>1\) 的时候，存在 stochastic rounding，这里有近似
      • 近似：把复杂的 \(\rho(\beta)\) 不管了
        • EARS 也使用了这种近似
    • \(\beta_t\le 1\) 不存在近似的
      • 【式子 2】

\[ \mathbb{V}\left[\langle I_t;\beta_t\rangle\right]= \left\{ \begin{array}{ll} \dfrac{1}{\beta_t}\mathbb{E}\left[\langle I_{t}\rangle^2\right]-\mathbb{E}^2\left[\langle I_{t}\rangle\right]&\text{if }\beta_t\le1 \\ \dfrac{1}{\beta_t}\mathbb{V}\left[\langle I_{t}\rangle\right]&\text{otherwise}\\ \end{array} \right. \]

proxy model

  • 在上面的近似之后，可以得到微分
    • 证明：根据 式子 1 展开，然后根据上面的 式子 2展开每一项

\[ \dfrac{\mathrm{d}\mathbb{V}\left[\langle I\rangle\right]}{\mathrm{d}\beta_t}= \left\{ \begin{array}{ll} -\dfrac{1}{\beta_t^2}\mathbb{E}\left[\langle I_{t}\rangle^2\right]+\sum_{k=1}^{n_t}\dfrac{1}{\beta_t}\dfrac{\mathrm{d}\mathbb{E}\left[\langle I_{k}\rangle^2\right]}{\mathrm{d}\beta_t}&\text{if }\beta_t\le1 \\ -\dfrac{1}{\beta_t^2}\mathbb{V}\left[\langle I_{t}\rangle\right]+\sum_{k=1}^{n_t}\dfrac{1}{\beta_t}\dfrac{\mathrm{d}\mathbb{V}\left[\langle I_{k}\rangle\right]}{\mathrm{d}\beta_t}&\text{otherwise}\\ \end{array} \right. \]

  • MIS 权重会存在 \(\beta_t\)，所以第二项很难计算
    • 论文只考虑 balance heuristic
  • 对于 budget-unaware MIS weights（MIS 权重不包含 \(\beta_t\)），第二项为 0，可以化简如下

\[ \dfrac{\mathrm{d}\mathbb{V}\left[\langle I\rangle\right]}{\mathrm{d}\beta_t}= \left\{ \begin{array}{ll} -\dfrac{1}{\beta_t^2}\mathbb{E}\left[\langle I_{t}\rangle^2\right]&\text{if }\beta_t\le1 \\ -\dfrac{1}{\beta_t^2}\mathbb{V}\left[\langle I_{t}\rangle\right]&\text{otherwise}\\ \end{array} \right. \]

  • 上述 proxy 是 bugdet-unware MIS 最优的
  • 如果是 budget-aware MIS，可能会偏离最优解
    • 做了两个实验说明问题，说明不考虑上面的第二项时，会出现问题
      • 差别不大（1D、实验）
      • 在应用中（PG、BDPT），比理论最优解更好
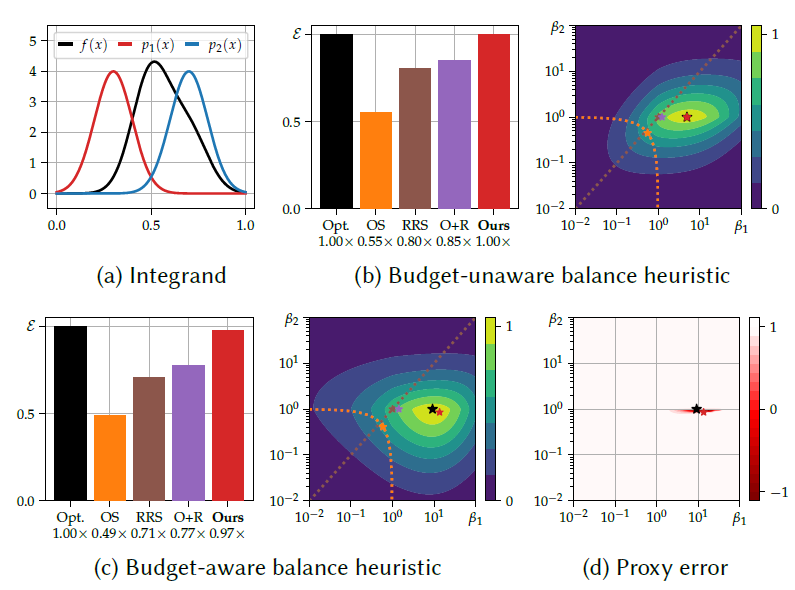
  • 下图是 1D 实验
    • 积分函数 \(f(x)\)
    • 两个采样 pdf \(p_1(x),p_2(x)\)
    • \(p_2\) 更好，但是慢 30x
    • 方法：OS（Optimal mixture sampling）、RRS、OS+RRS、Ours、Opt（理论最优）
      • OS+RRS 效果并不好，因为没有联合优化
    • （b）（c）热力图应该是表示 performance
    • （d）表示 （c） 中考虑/不考虑 MIS 中含有 \(\beta_t\) 的梯度 error（1 表示完全匹配）

不动点

  • 推导方式和 EARS 基本一致，结论也看着差不多
    • 【先不管，副录有证明】

\[ \beta_t= \left\{ \begin{array}{ll} \beta_{t}^{\mathrm{RR}}=\sqrt{ \dfrac{\mathbb{C}\left[\langle{I}\rangle\right]} {\mathbb{C}_t} \dfrac{\mathbb{E}\left[\langle{I_t}\rangle^2\right]} {\mathbb{V}\left[\langle{I}\rangle\right]}} &\text{if }\beta^{\text{RR}}<1 \\ \beta_{t}^{\mathrm{RR}}=\sqrt{ \dfrac{\mathbb{C}\left[\langle{I}\rangle\right]} {\mathbb{C}_t} \dfrac{\mathbb{V}\left[\langle{I_t}\rangle\right]} {\mathbb{V}\left[\langle{I}\rangle\right]}} &\text{if }\beta^{\text{S}}>1 \\ 1&\text{otherwise} \end{array} \right. \]

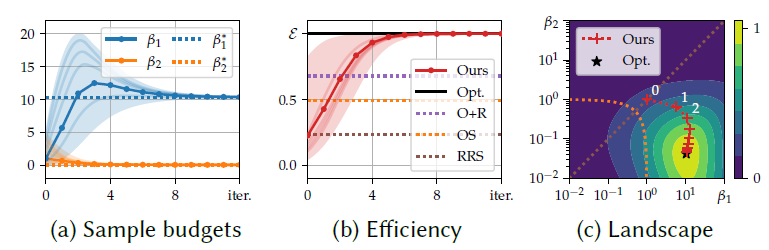
  • 解析解难算，使用不动点迭代求解
  • 收敛快，上面 1D 例子

Application to Path Tracing

  • Primary estimator

\[ \langle L_{\text{r},t}(x,\omega_{0})\rangle=\frac{\langle L_{\mathrm{i}}(x,\omega_{\mathrm{i}})\rangle\,B(x,\omega_{\mathrm{i}},\omega_{0})\left|\cos\theta_{\mathrm{i}}\right|}{p_t(\omega_{\mathrm{i}}\mid x,\omega_{0})}\;w_{t}(x,\omega_{\mathrm{i}},\omega_{\mathrm{o}}), \]

  • Secondary estimator
    • path prefix \(\bar{x}\)

\[ \langle L_\text{r}(x,\omega_{0})\rangle=\sum_{t=1}^{n_{t}}\frac{1}{\beta_{t}(\bar{x})}\sum_{s=1}^{\beta_{t}(\bar{x})}\langle L_{\text{r},t}(x_{s},\omega_{0})\rangle=\sum_{t=1}^{n_{t}}\langle L_{\text{r},t};\beta_{t}(\bar{x})\rangle \]

  • Random walks（PT 过程），递归
  • 效率定义：EARS 相同，var 使用 \(I_{\text{px}}^2\) 归一化
  • 优化：和上面类似

\[ \beta_t= \left\{ \begin{array}{ll} \beta_{t}^{\mathrm{RR}}= \dfrac{T(\bar{x})}{I_{\text{px}}} \sqrt{ \dfrac{\mathbb{C}_{\mathrm{I}}} {\mathbb{C}_t} \dfrac{\mathbb{E}\left[\langle{L_{\text{r},t}}\rangle^2\right]} {\mathbb{V}_\mathrm{I}}} &\text{if }\beta^{\text{RR}}<1 \\ \beta_{t}^{\mathrm{RR}}=\sqrt{ \dfrac{\mathbb{C}_{\mathrm{I}}} {\mathbb{C}_t} \dfrac{\mathbb{V}\left[\langle{L_{\text{r},t}}\rangle\right]} {\mathbb{V}_\mathrm{I}}} &\text{if }\beta^{\text{S}}>1 \\ 1&\text{otherwise} \end{array} \right. \]

  • \(T(\bar{x})\)：累乘
    • 相机响应函数、\(1/\text{pdf}\)、BSDF、MIS 权重

应用1-Path Guiding

  • NEE + BSDF + PPG
  • 基本上和 EARS 一样
  • PPG 的一轮迭代，认为是我们的一轮不动点迭代
  • local estimates
    • cost, variances, and second moments for each region and each technique
  • image statistics：OIDN denoiser
  • Fixed-point iteration
    • warm up：前 3 轮，throughput based RR + no Splitting
  • outlier clampling
    • 路径贡献 clamp <= 50 pixels color【只用于 local/image variance 估计】
  • \(\beta_t\)：[0.05, 20]
  • Handling colors：channel-wise 计算，然后乘在一起
    • perform computations channel-wise and use the \(L_2\) norm to compute the final sample counts【啥意思？】

Evaluation

  • path guiding：based on mixture optimization using gradient descent【Vorba et al. 2019】
  • EARS
  • 对比：throughput-based RR【5th bounce 开始】
  • 其他：1st bounce 开始
  • An ablation (“Ours + Grad. Descent”)【TODO】
    • combines gradientdescent (mixing BSDF and guiding) and our approach (sample counts of NEE and the mixture) to demonstrate that our approach chooses better mixtures than the previous state-of-the-art optimizer.
  • setup
    • 2.5min训练+2.5min测试
    • maxpath length：40
    • tree：72MB
    • 9 training iterations：time x2
    • relMSE 评估
    • 1% brightest outliers removal
  • 十个场景：1.32× 加速（相对 EARS）、17% fewer rays
    • 讲道理应该和 EARS+Optimal MIS 对比才有说服力
    • 我们的方法能够检测在不同的点，什么方法更差【然后降低他的采样数】
  • 收敛测试：我们算法能收敛到正确解

应用2-BDPT

  • 【略过，不太懂】

限制与展望

  • overhead：短时间训练，收集的统计信息不好，结果不好
  • Local estimates：outlier removal 太简单，参考更复杂的
    • 【EG-2018】Re-Weighting Firefly Samples for Improved Finite-Sample Monte Carlo Estimates
  • Discontinuity artefacts
    • Noise in the spatial caches
  • Proxy accuracy
  • Dynamic scenes
  • MIS weights：只考虑了平衡启发式
  • Correlated Techniques
    • 方差拆分认为是独立的，没有考虑相关的情况（photon mapping）
  • Applications outside of rendering
    • any Monte Carlo integration problem that relies on multi-sample MIS estimation