(论文)[2022-SIG] Deep Adaptive Sampling and Reconstruction using Analytic Distributions

Posted on Edited on In Views:
Deep Adaptive Sampling and Reconstruction using Analytic Distributions

DASR using Analytic Distributions

  • 主页：Disney Research | Studios, Switzerland
    • Farnood Salehi、Marco Manzi、Gerhard Röthlin、Christopher Schroers、Romann Weber、Marios Papas
  • 和之前的方法不同
    • 之前训练的图片是预渲染的，我们是从解析噪声中采样的（噪声近似像素分布）
    • 能够从少量目标分布的样本中高效采样
    • spp 增加，我们的解析近似越准
    • 另外还有 global summary module，用于获取感受野之外的信息（减缓局部最优问题）
    • 端到端训练：AS + Denoiser
  • 坚实的理论分析

Introduction

  • 理想的 AS 策略需要考虑：增加的样本如何影响 denoised image
    • 目前的 AS+ReCon 算法没有考虑这点【DASR】
  • 我们的算法比之前的效果更好：DEP、DASR（使用相同的训练数据集）
    • DEP：【2018-SIG】Denoising with Kernel Prediction and Asymmetric Loss Functions
  • 使用更少的训练数据，效果比 DASR 更好
    • 针对高质量的渲染时，减少 26-37% 的训练数据
  • 目标：We designed our method for the specific use case of high quality offline rendering of single frames, where the sampling distribution is refined iteratively during rendering.

Related Work

  • 我们的框架能使用任何可微的 denoiser，我们选用 KPCN
    • 【SIG-2017】Kernel-predicting convolutional networks for denoising Monte Carlo renderings
  • 最接近的两个工作：DEP、DASR
  • DEP：先估计降噪后图片的 remaining error，然后根据 error 获得 sampling map
    • 假设 error 的降低应该正比于目前的 denoising error（启发式）
      • 没有考虑当前像素样本的增加对周围像素的影响
    • denoiser 优化了 sampler，但是 denoiser 并没有从 sampler 中获得的分布中优化
  • DASR
    • 需要很多预渲染的训练样本
    • 因为磁盘 IO/GPU 显存问题，训练时间也被拉长
    • 多 spp 训练，这个问题更严重
  • 我们的方法类似 DASR，但是不需要存储大量样本

Methodology

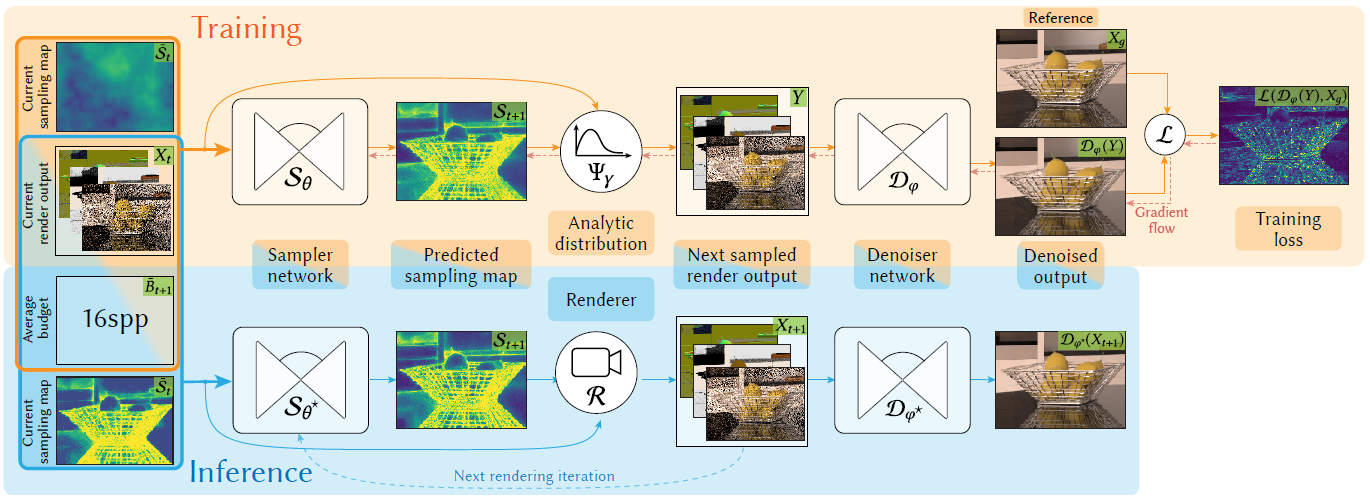
  • 迭代渲染：\(t\in[0,T]\)
    • 本轮迭代的样本数 \(B_t\)（budget）
      • \(B_t=\sum_{p\in P}s_p(t)\)
    • sample map \(\mathcal{S}_t=\{s_p(t)\}\)
  • 第一轮迭代：均匀分布
    • \(s_p(0)=B_0/|P|,\forall p\in P\)
  • 之后的 \(\mathcal{S}_t\) 计算如下

Optimizing the Sampling Map

  • 定义最优化目标

\[ \begin{aligned} &\quad\mathcal{S}_{t+1}(X_t, B_{t+1}) = \arg\min_{\mathcal{S}} \mathbb{E}_{Y \sim \mathcal{R}(Y | \mathcal{S}, \bar{ \mathcal{S}}_t, X_t)} \left[ \mathcal{L}(\mathcal{D}(Y), X_g) \right]&\quad(1)\\ \text{subject to}&\quad \sum_{p \in P} s_p = B_{t+1} \text{ and } s_p \geq 0, \forall p \in P&\quad(2) \end{aligned} \]

  • \(\mathcal{R}(Y | \mathcal{S}, \bar{ \mathcal{S}}_t, X_t)\)：根据 \(\mathcal{S}\) 生成新样本，并将其累加到 \(X_t\) 上之后的渲染结果分布
    • \(\bar{ \mathcal{S}}_t=\{\sum_{j=0}^{t}s_p(t)\}\)：累计 sample distribution
  • \(\mathcal{L}\)：loss
  • \(\mathcal{D}\)：denoiser
  • \(X_g\)：GT reference image
  • \(Y = \dfrac{\bar{\mathcal{S}}_t X_t + \mathcal{S} \bar{Y}_{\mathcal{S}}}{\bar{\mathcal{S}}_t + \mathcal{S}}\)（element-wise calculation）
  • 当前迭代轮 \(t\) 不知道下一轮迭代 \(t+1\) 的样本的值，因此 式子 1 得通过下一轮的期望优化
  • DASR 采样式子 1，\(Y\) 通过预渲染的图片组装
    • 需要保存所有样本，开销大

Analytic Noise Distribution Synthesis

  • 前提
    • 知道每一个像素的 GT mean、variance
    • renderer is using i.i.d. samples
  • 将（both） rendered and analytic distributions 建模为样本数的函数
    • 这样能够就能生成任意多的样本
  • 先分析 \(\mathbb{E}_{Y \sim \mathcal{R}(Y | \mathcal{S}, \bar{ \mathcal{S}}_t, X_t)} \left[ \mathcal{L}(\mathcal{D}(Y), X_g) \right]\) 的特征
  • \(X_t=[I_t,F_t]\)：noisy data（color、features）

引理1

  • 其中 \(\Psi\) 是任意和 \(\mathcal{R}\) 期望、方差相同的分布

\[ \begin{array}{l} \mathbb{E}_{\Psi\left(Y\mid\mathcal{S},\bar{\mathcal{S}}_{t}, X_{t}\right)}[Y]=\mathbb{E}_{\mathcal{R}\left(Y\mid\mathcal{S},\bar{\mathcal{S}}_{t}, X_{t}\right)}[Y],\\ \mathbb{V}_{\Psi\left(Y\mid\mathcal{S},\bar{\mathcal{S}}_{t}, X_{t}\right)}[Y]=\mathbb{V}_{\mathcal{R}\left(Y\mid\mathcal{S},\bar{\mathcal{S}}_{t}, X_{t}\right)}[Y]. \end{array} \]

  • 推导见论文，简单的理解如下
    • \(\text{MSE}=\text{Var}+\text{Bias}^2\)，然后发现最终的结果只和 \(\mathcal{R}\) 的 var、mean 有关，和 \(\mathcal{R}\) 本身无关
    • MRSE 可以写作 MSE 的表达式，剩余都是常量，因此也 OK
  • 引理1只是说，denoise kernel 不能依赖于 \(t+1\) 的某个具体的数据
    • 可以依赖于 \(t\) 和 \(t\) 之前已有的数据
    • 可以依赖于之后数据的一些统计信息
  • 在引理1的加持下，我们可以将 rendered samples 替换成任意的 mean、var 相同的解析分布 \(\Psi\left(Y\mid\mathcal{S},\bar{\mathcal{S}}_{t}, X_{t}\right)\)
  • 计算 future rendered mean、var
    • \(\hat{\mathbb{V}}[X_t]\)：numerical estimate of the variance of the current data
    • \(\mathbb{V}_{X_g}\)：reference sample variance【把样本数乘掉了，所以少了一个 \(\mathcal{S}\)】

\[ \mathbb{E}_{\mathcal{R}}(Y \mid \mathcal{S}, \bar{\mathcal{S}}_t, X_t)[Y] = \frac{\bar{\mathcal{S}}_t X_t + \mathcal{S} X_g}{\bar{\mathcal{S}}_t + \mathcal{S}} \]

\[ \mathbb{V}_{\mathcal{R}}(Y \mid \mathcal{S}, \bar{\mathcal{S}}_t, X_t)[Y] = \frac{\bar{\mathcal{S}}_t^2 \hat{\mathbb{V}}[X_t] + \mathcal{S} \mathbb{V}_{X_g}}{(\bar{\mathcal{S}}_t + \mathcal{S})^2} \]

Choice of Distribution

  • 前人研究表明，PT 结果，像素值均值的分布近似于 gamma 分布
  • 如下是示意图
    • 左右图只是低 spp 和 高 spp 的区别
      • 高 spp，gamma 分布近似的更好
      • 高 spp，分布更像是正态分布【中心极限定理】
    • 看左图
      • 上图：每个像素根据前 64 spp 的结果可以计算出一个分布 \(\mathcal{R}\)，然后根据 \(\mathcal{R}\) 进行采样 64 spp，得到的结果图
      • 下图：每个像素根据前 64 spp 的结果，使用分布 \(Y_{\gamma}\) 去近似这组数据，然后根据 \(Y_{\gamma}\) 进行采样 64 spp，得到的结果图
      • 选定了红绿蓝三个区域，将其放大后展示
        • 其中直方图对应被选中区域的中心像素，前 64 spp 的直方图【单个像素的直方图】
          • 展示其分布，红线表示近似的 gamma 分布

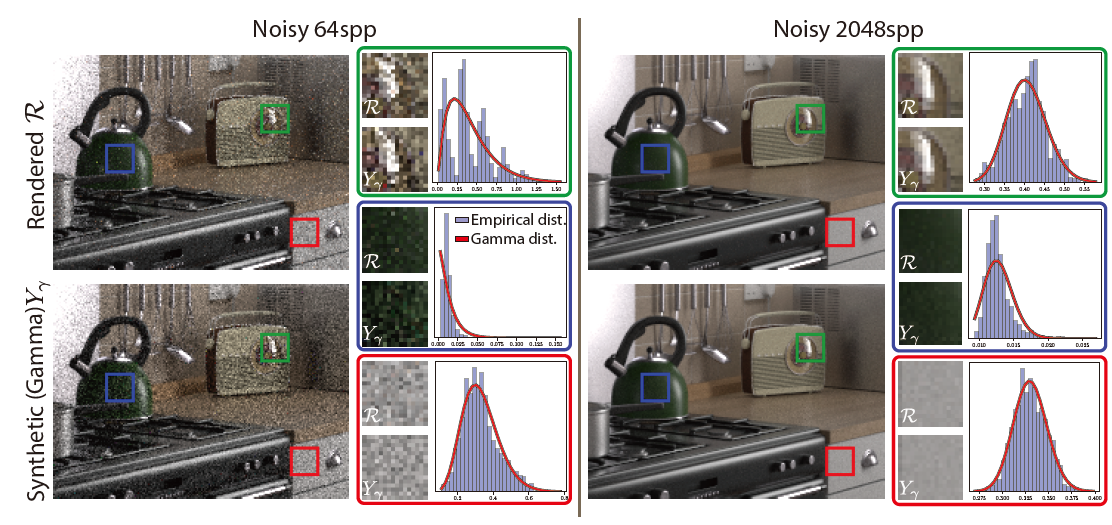
  • 对角线是真实的 CDF，另外 3 条线是近似情况
    • 可以看出 gamma、log-normal 在低 spp 也能不错近似

  • gamma 分布的好处
    • 期望：\(\alpha\beta\)，方差：\(\alpha\beta^2\)
    • gamma 分布的可加性
      • 相互独立的随机变量 \(X,Y\)，如果满足 \(X\sim \Gamma(\alpha_1,\beta);Y\sim \Gamma(\alpha_2,\beta)\)，则有 \(X+Y\sim \Gamma(\alpha_1+\alpha_2,\beta)\)
      • \(X_i\sim \Gamma(\alpha,\beta)\Rightarrow\sum X_i\sim \Gamma(N\alpha,\dfrac{\beta}{N})\)
  • 于是我们可以直接通过采样 ”mean distribution“ 得到均值（1 个样本就够了）
    • 不是本身就是 ”mean distribution“ 满足 gamma 分布吗？
      • 因为还需要采样若干个样本【例如 sample map 指示 4 个样本】
  • 采样新样本：\(Y_{\gamma}\sim\text{gamma}(\alpha(\mathcal{S}),\beta(\mathcal{S}))\)
  • 和现有样本进行加和

\[ \dfrac{\bar{\mathcal{S}}_t X_t + \mathcal{S} \bar{Y}_{\gamma}(\mathcal{S})}{\bar{\mathcal{S}}_t + \mathcal{S}}\sim\Psi_{\gamma}(Y|\mathcal{S},\bar{\mathcal{S}}_t,X_t) \quad(8) \]

  • 上面的式子 (8) 和 rendered data 有相同的 mean 和 var
    • 只需要 gamma 分布的均值为 \(X_g\)，方差为 \(\mathbb{V}_{X_g}/\mathcal{S}\)【根据方差、期望线性加和】
  • 计算 \(\alpha,\beta\)
    • \(\odot\) 表示 element-wise 的计算
    • 这和论文中差了一个倒数，估计论文中是使用 \(\gamma(\alpha,1\beta)\) 的这种表示方法，一样的

\[ \alpha(\mathcal{S}) = \frac{X_{g}^2 \odot \mathcal{S}}{V_{X_{g}}}, \quad \beta(\mathcal{S}) = \left(\frac{X_{g} \odot \mathcal{S}}{V_{X_{g}}}\right)^{-1} \]

  • 此时对于 式子 1，可以使用 \(\Psi_{\gamma}(Y|\mathcal{S},\bar{\mathcal{S}}_t,X_t)\) 代替 \(\mathcal{R}(Y | \mathcal{S}, \bar{ \mathcal{S}}_t, X_t)\)，从而更快的生成样本

Jointly Optimizing Sampling and Denoising

  • 上面说的方法，认为 \(\mathcal{D}\) 是固定的（fixed pre-trained denoiser）
  • 联合优化 \(\mathcal{D},\mathcal{S}\) 能够实现更低的 loss，式子 10

\[ \begin{aligned} &\arg\min_{\theta,\varphi} \sum_{\iota_t \in \mathcal{T}} \mathbb{E}_{Y \sim \Psi_Y \left( Y \mid \mathcal{S}_\theta(\bar{\mathcal{S}}_t, X_t, B_{t+1}), \bar{\mathcal{S}}_t, X_t \right)} \left[ \mathcal{L}(\mathcal{D}_\varphi(Y), X_g) \right]\\ \text{subject to}&\quad \sum_{p \in P} s_p = B_{t+1} \text{ and } s_p \geq 0, \forall p \in P&\quad(10) \end{aligned} \]

  • \(\iota_t=(X_t,\bar{\mathcal{S}}_t, X_g, B_{t+1})\)

Implementation

  • TensorFlow

Denoiser and Sampler Architectures

denoiser

  • two-pass kernel-predicting denoiser with a U-net architecture
  • two-pass：specular 和 diffuse 分开
    • diffuse 没有做 albedo division

  • UNet：5 scale
    • convolution bandwidths are 64, 128, 256, 256, 256
    • 输入图片：\(I\)（\(I_d/I_s\)，diffuse/specular）
    • 辅助信息：\(F_a\)（albedo）、\(F_n\)（normal）
    • 输入：\(X_t=\left[\log(1+I),\log(1+F_a),F_n\right]^\top\)
  • 输出 kernels

sampler

  • 架构类似，输入输出不一样
  • 输出一个标量：过一个 softmax

\[ \mathcal{S}_\theta(X_t, \bar{S}_t, B_{t+1}) = B_{t+1} \, \text{softmax}(\Phi_\theta(X_t, \bar{\mathcal{S}}_t, \bar{B}_{t+1})) \]

  • budget \(B_{t+1}\) 是一个重要的参数，对 sampling map 的影响是非线性的
  • 输入

\[ \tilde{X}_t = \begin{bmatrix} \log(1 + I_s) \\ \log(1 + I_d) \\ \log(1 + F_a) \\ F_n \\ \log(1 + \bar{S}_t) \\ \log(1 + \bar{B}_{t+1}) \end{bmatrix} \]

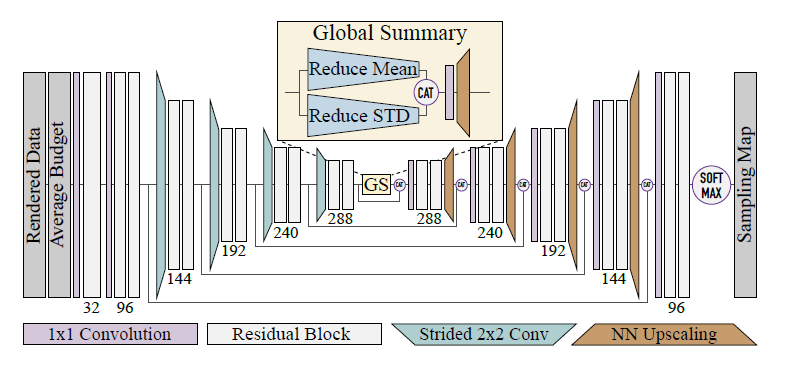
Global Summary Module

  • DASR 或者我们的简单实现，sampling maps 中存在 halos（晕），因为感受野太小导致的
  • 我们的解决方案：加上 global summary (GS) 模块
  • 放在 encoder 和 decoder 之间
    • 计算 encoder 的输出的统计量（相当于集成了所有像素的信息）
  • 流程
    • 对每个通道计算均值、标准差
    • concat
    • 1x1 conv 减小通道数
    • nearest-neighbor upscale 到和 decoder 输出 shape 相同
    • 和 decoder 输出 concat

Analytic Noise Distributions

  • 需要计算梯度
  • 可以通过 implicit re-parameterization 计算，但是非常不稳定
  • 同样我们也是用 DASR 的有限差分方式
  • 依赖于 \(\mathbb{V}_{X_g}\) 的准确估计（在渲染 GT 的时候高质量计算）
    • 最后再过一个 denoiser 去除 remaining noise【因为实际渲染的时候并得不到 GT】
    • variance denoiser 和 color denoiser 网络结构相似，也是在我们的训练集上训练，使用 SMAPE metric
      • \(\bar{\mathcal{S}}_t\cdot\mathbb{V}(X_t)\)：denoised sample variance estimate of \(X_t\)
      • \(\mathbb{V}_{X_g}\)：GT
  • 网络输入：\(\left[\log\left(1+\bar{\mathcal{S}}_{t}\cdot\mathbb{V}(X_{t})\right),\log\left(1+F_{\mathrm{a}}\right),F_{\mathrm{n}}\right]\)
  • 采样
    • RGB 通常认为是有相关性的，\(Y_{\gamma}\) 的每个通道使用相同的随机数种子进行采样
    • \(F_{\text{n}}\) 使用 Gaussian 采样，clamp 到 [-1, 1]（gamma 不能生成负值）
  • 测试了不同的解析分布
    • 发现 trunc.normal < log-normal < gamma（大于表示表现好）
    • 尤其在低 spp 下，gamma 表现更好
  • 实验性结论：减小噪声分布的方差，可以减小梯度反传的方差，但是会增大 bias
    • trade off：将 model variance /= 5

Dataset

  • 两个数据集
    • DASR：需要 cascaded spp 的图片
    • DEP/我们：正常
  • denoiser 都使用第二个数据集训练
  • 17 base scenes
    • 随机修改生成 4000 图
  • 程序化生成 sample map 用于训练（不同频率的 Perlin 噪声）
    • spatial variation in the sampling map 对于训练非常重要
  • DASR 需要 4x 磁盘空间
  • 数据增强：对 patch 进行 scale、channel 扰动
  • evaluation set
    • 24 手工制作的场景

Training

  • 2 phases：先训练 denoiser、然后一起训练
    • DEP 的 pretrained denoiser 不再训练
  • patch size 128x128；mini-batch size 4

Denoiser Training

  • color
    • five-scale kernel-based denoiser
      • 输出 kernel weights
      • 5 scale 是指和 2018 那篇上采样下采样拼出来一样的吧？
    • loss 和 DASR 相同
      • L：Laplacian of Gaussian operator（边缘检测），可以认为是一种 perceptual loss
      • \(x'=\log(x+1)\)：logLoss

\[ \ell({x^{\prime}},{X_{g}}^{\prime})=0.5\left\Vert\frac{x^{\prime}-X_{g}^{\prime}}{X_{g}^{\prime}+\epsilon}\right\Vert_{1}+0.5\left\Vert\frac{L({x^{\prime}})-L(X_{g}^{\prime})}{X_{g}^{\prime}+\epsilon}\right\Vert_{1} \]

  • variance denoiser：SMAPE loss
  • 训练：
    • 2M iters，Adam，lr=2e-5
    • fine-tune：250K iters，lr/=10 each phase

联合优化

  • 直接优化 式子 10，效果不太好
    • 我们的训练是基于合成数据，推理是真实数据
    • \(\mathcal{L}\)：logLoss
  • \(X_t\) 是真实数据【？不是累加的结果吗？】

\[ \begin{aligned} &\arg\min_{\theta,\varphi} \sum_{\iota_t \in \mathcal{T}} \mathbb{E}_{Y \sim \Psi_Y \left( Y \mid \mathcal{S}_\theta(\bar{\mathcal{S}}_t, X_t, B_{t+1}), \bar{\mathcal{S}}_t, X_t \right)} \left[ \mathcal{L}(\mathcal{D}_\varphi(Y), X_g) {\color{red}+\mathcal{L}(\mathcal{D}_\varphi(X_t), X_g)} \right]\\ \text{subject to}&\quad \sum_{p \in P} s_p = B_{t+1} \text{ and } s_p \geq 0, \forall p \in P&\quad(10) \end{aligned} \]

  • fine-tune 阶段：每次迭代同时更新 sample map estimator 和 denoiser（DASR 交替更新）
    • 效果不会变差，反而可以减少网络收敛的训练轮次

结果