(论文)[2011-SIG] Adaptive sampling and reconstruction using greedy error minimization

Posted on Edited on In Views:
提出了一个适应性采样+重建图片的框架并给出了一个算法；是一个迭代算法，分为初始化和适应性采样两个阶段；适应性采样节点，每次迭代，对于每一个像素，根据生成的样本从预定义的若干个（5-8）Gaussian Filter 中找到最优的 Filter，然后根据 Filter 的结果再去重新分配光线（可以理解为更新 sampling map），直到资源用尽迭代结束。

GEM-AS

  • Adaptive sampling and reconstruction using greedy error minimization
  • 作者：Fabrice Rousselle、Claude Knaus、Matthias Zwicker
    • University of Bern
  • 任务：Adaptive Sampling + Construction

Introduction

  • 问题形式化描述
    • given a certain budget of Monte Carlo samples, obtain an image that minimizes the relative mean squared error (MSE) by distributing samples in a suitable fashion in the image plane and by filtering the image with appropriate filters.
  • 在样本分布空间 + filter 空间的优化问题
    • filters 预定义，但是每个像素可以不一样
    • 不同尺度的 Gaussians
  • 贪心算法：2 steps 的迭代法
    • 样本分布确定，从离散的 filters 中找到最小化 MSE 的一个
    • 在确定 filters 的情况下，找到更好的样本分布
  • 不保证无偏性
  • 与 MCPT 的各种优化正交
  • 贡献
    • 提供了 AS+Recon 的框架
    • 提供了框架的一种实现
    • 从噪声中获取统计量

Previous Work

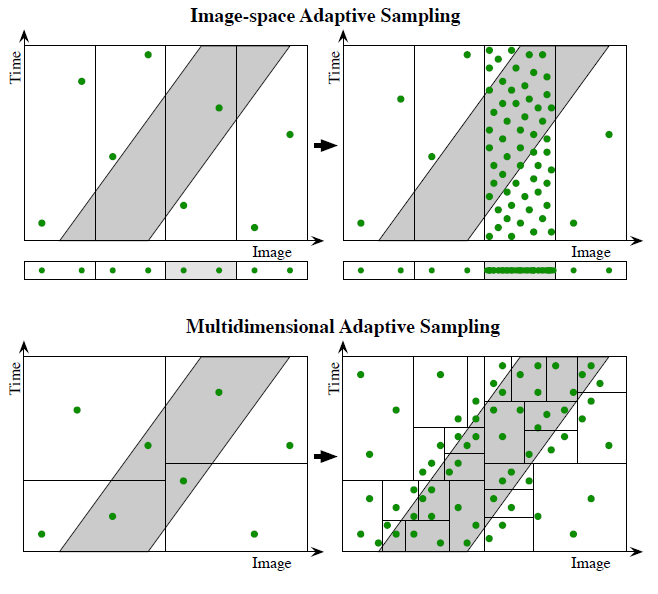
  • Image Space Adaptive Sampling and Reconstruction
    • 先驱：【1987-SIGC】Generating antialiased images at low sampling densities
    • 【2003】Bala：显式表示边，实现 interactive rendering
    • 【1998】Bolin and Meyer：通过 Haar wavelets，提出了基于感知的误差
    • sota【2009】Overbeck：Adaptive wavelet rendering (AWR)
      • 和我们思想相似，但是局限于小波【ToBeRead】
      • 启发式找到样本分布
  • Multidimensional Adaptive Sampling and Reconstruction
    • 【2008】Hachisuka：直接在高维空间中做 AS【curse of dimension】
      • 这里的高维空间似乎指的是 distributed effects

  • Adaptive Filtering
    • 不管 AS，直接重建（类似现在的降噪工作等），会导致焦散等信息缺失
    • 【2009】Ritschel：cross bilateral filtering
    • 【2010】Dammertz：an edge-avoiding a-trous wavelet transform
    • 【2011】Shieley：使用 depth buffer
  • Image Denoising
    • 【1994】Wavelet shrinkage：通过小波变化去除噪声（噪声是 small coefficient）
    • 假设一种噪声模型，然后对其降噪

Algorithm Overview

Filter Selection

Incremental MSE Minimization

  • 这一小节表示我们不需要 GT 信息

\[ \text{MSE}[c]=\text{Bias}[c]^2+\text{Var}[c] \]

\[ \begin{array}{l} \text{MSE}[c]=\mathbb{E}\left[\left(c-\bar{c}\right)^2\right]\\ \text{Bias}[c]^2=\left(\mathbb{E}\left[c\right]-\bar{c}\right)^2\\ \text{Var}[c]=\mathbb{E}\left[\left(c-\mathbb{E}(c\right)^2\right]\\ \end{array} \]

  • 直接估计 filter 的 bias 很难（需要 GT 信息），而 variance 相对简单（不需要 GT 信息）
  • 考虑我们的 filters 可以通过 uniform scale 相关联
    • 排序：fine to coarse（sharp to smooth）
  • key observation
    • 随着 filter（fine \(\to\) coarse），bias 单增，variance 单减（单调性假设）
  • 定义变换：\(\Delta\) 表示，在计算 bias 的时候与不需要真值
    • scale selector \(\mathcal{S}\)

\[ \begin{array}{rl} \mathcal{S}=\Delta{\text{MSE}}\left[f\to c\right]&=\text{MSE}\left[c\right]-\text{MSE}\left[f\right]\\ &=\text{Bias}\left[c\right]^2-\text{Bias}\left[f\right]^2+\text{Var}\left[c\right]-\text{Var}\left[f\right]\\ \end{array} \]

  • 选取最好的 filter
    • five scales of Gaussian filters at dyadic in tervals
    • 根据单调性：\(\mathcal{S}\) 一旦为正，最优的就是当前的 \(f\)，否则继续
  • 我们使用 Bias、Var 的真值进行验证，我们的假设对于 99.7% 的像素成立

Quadratic Approximation

  • 假设 GT 是 filter 内像素的二次函数，filter 的一阶中心距为 0，于是有
    • \(r_c,r_f\) 表示 coarse、fine 的 filter 的 scale
    • 直观理解：filter scale 2x，Bias 变成 4x【具体为啥不太懂】

\[ \text{Bias}[c]=\dfrac{r_c^2}{r_f^2}\text{Bias}[f] \]

  • 连立上式和 \(\text{Bias}[c]=c-\xi,\text{Bias}[f]=f-\xi\)

\[ \text{Bias}[c]^2-\text{Bias}[f]^2=\dfrac{r_c^2+r_f^2}{r_c^2-r_f^2}(f-c)^2 \]

  • \(\mathcal{S}\) 的第一项解决
  • 我们的二次函数假设对于 82.8% 的像素成立
    • 真值验证：从所有候选 filters 中选取最优的（exhausted）
  • 对比了 incremental 方法和我们方法和 exhausted 方法的一致程度
    • incremental 更好（不知道这是啥，论文也没写）

Estimation from Noisy Data

  • \(f,\text{Var}[f]\) 都未知，需要估计
  • 样本 \(s_i\)

\[ f=\sum_{i\in\{1\ldots s\}}w_i^f\,s_i \]

\[ \text{Var}\left[f\right]=\sum_{i\in\{1\ldots k\}}\left(w_{i}^{f}\right)^{2}\text{Var}\left[s_{i}\right] \]

  • 每一个样本的方差估计如下，对像素内的样本计算

\[ \text{Var}\left[s_{i}\right]\approx\frac{1}{\left|P\right|-1}\sum_{j\in\{P\}}\left(s_{j}-\bar{s}\right)^{2} \]

  • \(\mathcal{S}\) 的第二项解决

实验

  • 分析如果样本满足一定假设 \(\mathcal{S}\) 的行为
    • 很难，如下做数值分析
  • 实验
    • 样本 \(s_i\)：value zero and additive noise
    • fine 是 coarse 的 2x
    • 输入：\(P\)、fine 的半径 \(r\)、样本 \(s_i\) 噪声的方差
  • 理想决策：coarse（因为 bias=0）
    • error rate：\(\mathcal{S}\) 犯错的比例
  • 实验目的：理解 \(\mathcal{S}\) 随着输入的变化，从而找到一个好的参数
  • bias term 和 variance term 是独立的，于是可以分别计算【所有样本都是独立的，使用不同样本就是独立的】
  • error rate 实验结果
    • Sample Variance
      • error rate 和噪声的方差无关：都是成正比（好的不会变差）
    • Filter Radius
      • 弱相关，large scale 较低
    • \(P\)：少了不行，多了差不多
      • bias \(\propto 1/P\)
  • 参数选择：bias term 加上权重 \(\rho\cdot z(\gamma)\)
    • \(\rho=1-1/\vert{P}\vert\)：修正 low sample counts
    • \(z(\gamma)=-\log(1-(1.9\gamma)^{1/\sqrt{2}}),0<\gamma<0.4\)
      • \(\gamma\) 表示 error rate，用户指定（Bias 和 Var 之间的 trade off）

Post-Processing the Filter Selection

  • non-zero error rate 都会导致 wrong filter selection decisions，在最终结果图上展现出 spikes 的 artifacts
    • 效果就是更平滑
  • 实验场景：1D、250 pixels、8 Gaussian filters（\(\sqrt{2}\) x）、输入为两个方形信号（uniform noise）
  • 相当于给 filter size 做一个降噪
    • 举例：如果一个像素周围都选第一个 filter，只有这个像素选择第 8 个，则认为选择有问题
  • outlier：孤立出现
  • 我们处理方式：Gaussian filter（coarse size）之后四舍五入
    • 论文中说或许可以进一步研究
  • 实际 2D 例子如下
    • binary stop from scale 2 to 3：白色表示选择 2，黑色表示需要进一步 coarse

Sample Distribution

  • 选中 m 个像素，使得 relMSE 能够降低的最多（每个像素分配 n 条光线）
  • 先估计 MSE，relMSE 使用 \(\dfrac{\text{MSE}}{\epsilon+\text{ref}^2}\)
    • \(\epsilon=0.001\)：prevent overemphasizing very dark image areas
  • relMSE 反比于样本个数
  • \(n_s\) 个样本，再来 \(n\) 个样本，relMSE 降低了：relMSE\(\times \dfrac{n}{n+n_s}\)
  • 算法步骤
    • 维护一个优先队列，每次选出能够让 relMSE 降低最多的 m 个像素
      • 假设 filter 是没有 overlap 的，但是并不强求（相当于一个启发式）
    • 对每个像素，在他的 support 中根据 filter 的权重重要性采样 n 个点，每个点采样一条光线
  • 为了计算降低的 relMSE，每个像素需要维护一个数（样本的个数）

Implementation

  • Computation of Scales and Their Statistics
    • 计算 Var 的时候，不可能保存所有样本，因此每个像素保存 finest filter scale、样本方差的均值（每次迭代更新）

\[ \text{Var}\left[p\right]\approx\frac{1}{\left|P\right|}\frac{1}{\left|P\right|-1}\sum_{j\in\{P\}}\left(s_{j}-\bar{s}\right)^{2} \]

  • Filtering Non-Uniform Sample Distributions
    • 我们的 sample density map 在 edge 的地方变化大，可能会得导致大的 bias
    • 参考【1987-SIG】Generating antialiased images at low sampling densities
    • 使用 subpixel grid【4x4】，subpixel 的值使用 subpixel box filter 得到，内部均匀采样
      • 相当于分层采样了，省的边缘 density map 变化大
  • Final Reconstruction
    • 最后一次迭代，filter selection 有一些区别
      • 使用 8 Gaussian（\(\sqrt{2}\)x）,finest 标准差 1.0，这样可以让最终的选择的 scale 更平滑
      • binary stopping map，使用更大的 Gaussian，2x coarse【smoother】
      • 只有在需要继续 coarse 的时候，才使用 filtered binary map（能停就停了，除 spike 效果更好）
  • 在 PBRT 中实现
    • initialization state：4 spp uniform
    • adaptive state：8 次迭代，用户指定需要渲染 \(n\) spp
      • 每次迭代分配样本：\(N=M(n-4)/8\)，\(M\) 表示像素个数
      • 每次选择分配给 \(m\) 个像素 \(n\) 个样本，\(m=N/n\)

Result

  • \(\gamma=0.1\)
  • dual 4-cores XEON system at 2.50GHz, with 8GB of RAM
  • \(\gamma\)
    • 小：smooth + blur edge
    • 大：keep edge + outlier
    • 0.2-0.3 之间，MSE 变化都不大（平衡）
  • relMSE：\(\epsilon=0.01\)
  • Discussion and Limitations
    • 如果 PT 很难找到特殊光路，则会低估方差
    • 渲染器出来的结果并不是完全随机的，因此会高估方差
    • 边界处理不是很好（我们用的各向同性的高斯 filter）