(论文)[2022-SIGC] Denoising-Aware Adaptive Sampling for Monte Carlo Ray Tracing

Posted on Edited on In Views:
DASR 等基于神经网络的 AS+ReCon 工作，在生成 sampling map 的时候只依赖于 1 spp noisy 图片，对于降噪后的图片方差则没有太多考虑；论文提出了一种根据降噪输入数据的方差估计降噪后输出的方差的方法，然后根据输出的方差去引导 AS，取得了更好的效果；论文方法能够很好的与最近的方法结合，也不需要额外的网络；论文使用的降噪器是 Intel 预训练的的 OIDN

Denoising-Aware Adaptive Sampling

  • Denoising-Aware Adaptive Sampling for Monte Carlo Ray Tracing
  • 作者：Arthur Firmino、Jeppe Revall Frisvad、Henrik Wann Jensen
    • 1、2：Technical University of Denmark
    • 1、3：Luxion
  • 我们的方法
    • 可以进一步提高 deep-learning based denoising 的效果
    • 不需要额外的网络或者学习
  • 最大的贡献：当网络的输入是随机变量的时候，能够估计网络输出的方差
  • 使用估计的方差迭代的生成样本

Introduction

  • 就算硬件加持，MCPT 还是很难实时
  • image denoise
    • 早期：通过 auxiliary features, sample statistics, and error estimates 优化参数
    • 后期：NN，大部分基于 CNN
  • sample variance 在屏幕空间不是均匀的 => Adaptive Sampling
    • 早期：AS+Denoise，利用 Denoise 后的方差/误差指导 AS
    • 后期：Sampling Map Estimator Net + Denoise Net
      • 问题：AS 更像是网络学习出来的得以函数，而和最终图像的方差关系不大
        • Sample Map 生成喝 Denoised Image 的关系不大（输入中没有这个）
  • 我们：NN + variance estimate（bridge the gap）
    • 基于 denoiser 的一阶泰勒展开
    • 通过前向自动微分、Jacobian 计算
    • 在渐近渲染的过程中，会时常考虑 denoised image 的结果
      • tonemapped version 也 ok（也可以作为一部份）

Related Work

Monte Carlo Denoising

  • 早期：a variety of non-linear filters
  • 后来：考虑辅助信息（surface normals, albedo, pixel variance, estimates of reconstructed error）
  • NN：各种各样
    • prediction of filter parameters
    • entire filter kernels
    • direct prediction of radiance values and coupling denoising with supersampling
      • denoise + super sampling
    • 针对低 spp
    • 高 spp 无偏研究，post-correction techniques
      • combining multiple denoised images
      • training a network on error estimates to infer blending parameters between rendered and denoised images
      • James-Stein theory, using a network to help estimate the variance of the unbiased input

Adaptive Sampling

  • 更类似后验的方法，根据 denoised image 的性质反馈 AS【之前的 SURE12】
    • 我们将其迁移到网络上
  • 低 spp
    • DASR、时序 DASR
    • 训练的时候能用更高 spp 图片
      • 【SIG22】Deep Adaptive Sampling and Reconstruction using Analytic Distributions
    • 通病：sampling map 的好坏和 denoised 的图片相关不大， 因此泛化性较差（原论文说有）

Statistical Estimates for Denoised Images

  • 主要是 variance and error

Double-Buffer

  • 独立渲染两张图 \(\mathbf{x}_a,\mathbf{x}_b\)
  • Double-Buffer Variance Estimate
    • 展开就推出来了

\[ \text{Var}\left[f_i(\mathbf{x})\right] = \frac{1}{2} \mathbb{E} \left[ \left( f_i(\mathbf{x}_a) - f_i(\mathbf{x}_b) \right)^2 \right] \]

  • Double-Buffer Error Estimate
    • \(\hat{\sigma}_{a,i}^2,\hat{\sigma}_{b,i}^2\) 表示方差的无偏估计

\[ \mathbb{E}\left[(f_i(\mathbf{x}) - \mu_i)^2\right]=\mathbb{E}\left[\frac{1}{2}\left((f_i(\mathbf{x}_a) - \mathbf{x}_{b,i})^2 - \hat{\sigma}_{b,i}^2 + (f_i(\mathbf{x}_b) - \mathbf{x}_{a,i})^2 - \hat{\sigma}_{a,i}^2\right)\right] \]

  • 证明：PT 出图 \(x_a,x_b\)，降噪结果 \(f(x)\)，真值 \(\mu\)，方差 \(\sigma\)

\[ \begin{aligned} \mathbb{E}[(f(x_a)-\mu)^2] &=\mathbb{E}[(f(x_a)-x_b+x_b-\mu)^2]\\ &=\mathbb{E}[(f(x_a)-x_b)^2]+\mathbb{E}[(x_b-\mu)^2]+2\mathbb{E}[(f(x_a)-x_b)(x_b-\mu)]\\ &=\mathbb{E}[(f(x_a)-x_b)^2]+\sigma^2+2\mathbb{E}[(f(x_a)-\mu+\mu-x_b)(x_b-\mu)]\\ &=\mathbb{E}[(f(x_a)-x_b)^2]+\sigma^2+2\mathbb{E}[(f(x_a)-\mu)(x_b-\mu)]-2\mathbb{E}[(x_b-\mu)^2]\\ &=\mathbb{E}[(f(x_a)-x_b)^2]-\sigma^2+2\mathbb{E}[(f(x_a)-\mu)(x_b-\mu)]\\ &=\mathbb{E}[(f(x_a)-x_b)^2]-\sigma^2+2\mathbb{E}[f(x_a)(x_b-\mu)]-2\mu\mathbb{E}[(x_b-\mu)]\\ &=\mathbb{E}[(f(x_a)-x_b)^2]-\sigma^2+2\mathbb{E}[f(x_a)]\mathbb{E}[(x_b-\mu)]-0\\ &=\mathbb{E}[(f(x_a)-x_b)^2]-\sigma^2+2\mu\cdot0\\ &=\mathbb{E}[(f(x_a)-x_b)^2]-\sigma^2\\ \end{aligned} \]

  • 上面两种方式都没有用到降噪后的结果：\(f\left(\frac{1}{2}(\mathbf{x}_a + \mathbf{x}_b)\right)\)

SURE

  • \(\mathrm{x}\) 是正态分布
    • estimated covariance matrix of \(\mathrm{x}\)

\[ \mathbb{E}\left[(f_i(\mathbf{x}) - \mu_i)^2\right] = \mathbb{E}\left[(f_i(\mathbf{x}) - \mathbf{x}_i)^2 + 2(\mathbf{J}_f(\mathbf{x}) \hat{\Sigma})_{i,i} - \hat{\sigma}_i^2\right] \]

Denoising-aware AS

  • 估计 NN 的 variance

Deep NN Variance Estimate

  • 目的：不使用 double buffer、降低 variance 估计的噪声
  • 函数：\(f_i:\mathbb{R}^N\to\mathbb{R}\)
    • 输入是独立的随机变量 \(X_1,\cdots,X_N\)，各自的方差为 \(\text{Var}\left[X_j\right]=\sigma_j^2\)
    • 则输出方差的一阶估计如下
      • 根据 \(\text{Var}[f(x)]=\text{Var}[\Delta f(x)]\)，泰勒展开即证

\[ \text{Var}[f_i(X_1, ..., X_N)] \approx \sum_{j=1}^{N} \left|\frac{\partial f_i}{\partial x_j}\right|^2 \sigma_j^2. \]

  • 微分和 JVP（Jacobian-vector product）同义
  • NN 函数 \(f:\mathbb{R}^N\to\mathbb{R}^M\)
    • \(\mathbf{v}\in\mathbb{R}^N\) 在 \(\mathbf{x}\in\mathbb{R}^N\) 处的 JVP 为 \(\mathbf{J}_f(\mathbf{x}) \mathbf{v} \in \mathbb{R}^M\)
      • \(\mathbf{J}_f(\mathbf{x}) \in \mathbb{R}^{M\times N}\)
      • \(\mathbf{J}_f(\mathbf{x})_{i,j}=\dfrac{\partial f_i}{\partial x_j}(\mathrm{x})\)
  • 我们取 \(\mathbf{v}\) 如下：\(v_j = \{+\sqrt{\hat{\sigma}_j^2}, -\sqrt{\hat{\sigma}_j^2}\}\)，均匀采样
    • 其中：\(\hat{\sigma}_j^2\) 是 \(\sigma_j^2\) 的无偏估计
    • 于是有
      • \(\mathbb{E}\left[v_j\right]=0\)
      • \(\mathbb{E}\left[v_jv_k\right]=\mathbb{E}\left[v_j\right]\mathbb{E}\left[v_k\right]=0,j\ne k\)

\[ \begin{align*} \mathbb{E}\left[\left(\left(\mathbf{J}_f(\mathbf{x})\mathbf{v}\right)_i\right)^2\right] &= \mathbb{E}\left[\left(\sum_{j=1}^{N} \frac{\partial f_i}{\partial x_j}(\mathbf{x}) v_j\right)^2\right] \\ &= \mathbb{E}\left[\sum_{j=1}^{N} \left|\frac{\partial f_i}{\partial x_j}(\mathbf{x})\right|^2 v_j^2 + 2\sum_{j=1}^{N} \sum_{k=1}^{j-1} \left(\frac{\partial f_i}{\partial x_j}(\mathbf{x}) \frac{\partial f_i}{\partial x_k}(\mathbf{x})\right) v_j v_k \right] \\ &= \sum_{j=1}^{N} \left|\frac{\partial f_i}{\partial x_j}(\mathbf{x})\right|^2 \mathbb{E}[v_j^2] + 2\sum_{j=1}^{N} \sum_{k=1}^{j-1} \left(\frac{\partial f_i}{\partial x_j}(\mathbf{x}) \frac{\partial f_i}{\partial x_k}(\mathbf{x})\right) \mathbb{E}[v_j v_k] \\ &= \sum_{j=1}^{N} \left|\frac{\partial f_i}{\partial x_j}(\mathbf{x})\right|^2 \sigma_j^2 \approx \text{Var}[f_i(X_1, ..., X_N)]. \end{align*} \]

  • JVP 的计算：在 NN evaluate 的时候能够同时计算
  • 之前有人提出类似的，但是我们更快，我们只需要传递一个 scalar（他需要传递每一个多元泰勒的系数）

Denoising-Aware AS

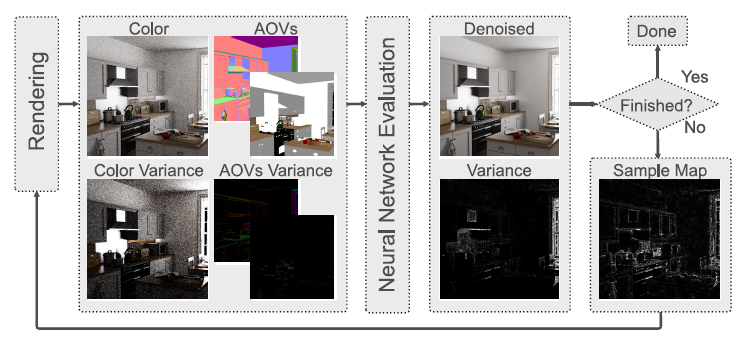
  • 任意寻找一个基于 NN 的 denoiser
    • initialization state：均匀采样
    • rendering state：denoise accumulated 图像的同时计算 \(f(\cdot)\) 的 variance
  • 然后按照公式操作，得到新图
    • \(N_i\)：累计的 spp 数目，增加 1 spp，带来的 Var 的降低
    • relative（处理 unbounded image、避免过度优化过亮区域）：\(\epsilon=0.01\)

\[ \frac{\text{Var}[f_i(\mathbf{x})]}{(N_i + 1)(f_i(\mathbf{x})^2 + \epsilon)},\quad(3) \]

  • 得到新图后
    • \(\max(v,0)\)
    • \(\sigma=0.5\)，\(5\times5\)，gaussian filter：避免强烈的不连续性
    • 归一化

Denoising with Post-Correction

  • 我们的方差估计可以很好的和最近的工作相结合：Neural James-Stein (NJS) combiner
  • NJS 框架
    • 无偏估计：\(\mathrm{x}_a,\mathrm{x}_b\)；降噪后的结果：\(f(\mathrm{x}_a),f(\mathrm{x}_b)\)
    • \(f(\mathrm{x}_a),f(\mathrm{x}_b)\) 根据预测的 \(\alpha_i\) 进行混合
    • 然后再和 \(\mathrm{x}=\left(\dfrac{\mathrm{x}_a+\mathrm{x}_b}{2}\right)\) 进行混合，混合系数 \(\rho_i\)（根据 James-Stein 理论计算得到）

\[ \rho_i(\alpha_i f(\mathrm{x}_a)+(1-\alpha_i)f(\mathrm{x}_b))+(1-\rho_i)\mathrm{x} \]

  • 方差如下：所有的都能计算

\[ \rho_i^2 (\alpha_i^2 \text{Var}[f_i(\mathbf{x}_a)] + (1 - \alpha_i)^2 \text{Var}[f_i(\mathbf{x}_b)]) + (1 - \rho_i)^2 \text{Var}[\mathbf{x}] \]

  • 计算完成之后，替换 式子 3 的分子，然后进行 AS
  • 区别
    • 这里我们忽视了 \(\rho_i,\alpha_i\) 本身也是随机变量（合理的，本身方差小）
    • 忽略了 regression-based optimization（让 \(\mathrm{x}\) 在低 spp 中更好）
      • 因为不忽略的话需要额外计算优化后图片的方差

Tone Mapping

  • map to \([0,1]\)
  • 相当于在 denoiser 外在套一个函数即可
  • tone-mapping：\(\mathcal{T}:\mathbb{R}^N\to\mathbb{R}^N\)
  • 于是整个过程：\(f_{\mathcal{T}}(\mathrm{x})=\mathcal{T}(f(\mathrm{x}))\)
  • 计算梯度

\[ \frac{\partial}{\partial x_i} f_{\mathcal{T}_i}(\mathbf{x}) = \sum_{k=1}^{N} \left(\frac{\partial}{\partial f_k} \mathcal{T}_i(f(\mathbf{x})) \frac{\partial}{\partial x_j} f_k(\mathbf{x})\right) \]

  • 此时再使用 公式 3 的时候，不需要再除以 \(f(\mathrm{x})^2\) 进行 relative 了（有界了）

Implementation

  • PyTorch
    • forward auto-differentiation (autodiff) 计算 JVP
    • 网络实现，UNet + OIDN(v1.4.3 预训练的权重)
      • 时间 3x longer than evaluating the Net
  • 网络实现，可以换成任意的之前的 NN denoiser
    • 时间大部分情况下和网络梯度反传差不多
  • NJS 比较的时候，因为他们不是 pytorch 实现的，我们略去了 130ms 的切换 context 的时间【合理比较】
    • 实现问题
  • Mitsuba 3，2x2 block size
    • AS 的时候，可能花更多时间渲染（复杂光路多 spp），这部分时间我们在对比的时候加上了
  • 做了不同迭代轮的实验：spp \(4\to128\)
    • 迭代轮越多，效果越好（足够之后，效果增加有限），但是上下文次数增加切换导致开销变大（render/denoise）
    • 我们的 balance：32spp

AS with MC-SURE

  • 计算 NN 的 SURE 系数，没有 denoiser 的 closed form，不能像 【2012-SURE-AS】那么计算
    • 他的中间项是对角矩阵，直接就等价于 \(\sigma^2\mathbf{I}\)【不太懂具体原理】
  • 参考 【EG2022】Progressive Denoising of Monte Carlo Rendered Images，利用【2008-MC-SURE】计算
    • 一阶泰勒近似

\[ (\mathbf{J}_f(\mathbf{x}) \cdot \hat{\Sigma})_{i,i} \approx \frac{1}{\epsilon K} \sum_{k=1}^{K} \left(b_k^T (\mathbf{f}(\mathbf{x} + \epsilon \mathbf{b}_k) - \mathbf{f}(\mathbf{x}))\right)_i \]

  • \(b_k\sim\mathcal{N}(0,\hat{\Sigma})\)，\(\epsilon=10^{-4}\)，\(K=4\)（估计的样本数）
  • 这样就将 SURE-AS 从显式的滤波函数推广到了 NN
  • 使用 SURE 的时候，将 式子 3 的分子替换成 SURE 估计的 MSE
    • 噪声更大，gaussian filter 需要更大（17x17，\(\sigma=4.0\)）

Results And Discussion

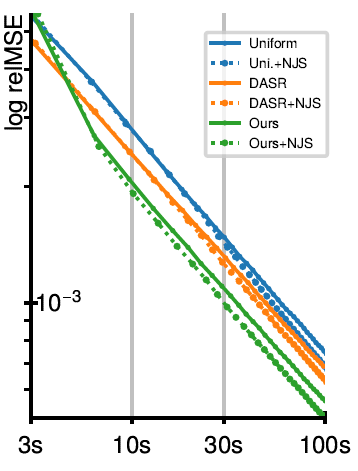
  • equal-time
  • 32-core CPU 渲染，RTX 3090 降噪
  • metric：relMSE，\(\epsilon=0.01\)
    • tone mapping 的时候，使用 RMSE（Root MSE）

实验

  • Path Tracing with Denoising（作为 baseline）：我们 > MC-SURE > DASR

    • 比 MC-SURE 好
      • 我们的 variance estimate 的方差比 MC-SURE 更小（估计本身带有方差）
      • 使用 variance 做 AS 比使用 error 更好（NN 输入的 variance 和 输出的 variance 有明确关系）
    • 比 DASR 好
      • DASR 只从1spp 中估计 sample map，缺乏可靠信息

  • Post-Correction Denoising：和 NJS 结合

    • 我们 > MC-SURE > DASR

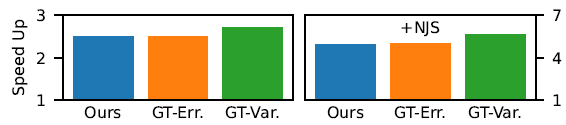
  • Comparison to Ground-Truth Sampling

    • GT：每次迭代结束，通过 32 张累计的图片降噪后，计算估计（not impractical）
    • 显示我们的方法和 GT 差不太多
    • 同时说明：AS 正比于 Var 比 正比于 Error 更好（下图）
    • 另外：虽然和 GT 相比，我们的估计还是有噪声的，但是效果上来说还行

  • Tone Mapping：ACES
    • 有界 => error 评估 RMSE
    • visual error 越大样本越多
    • 使用不同的 metric 作为 guiding AS，效果不一样
      • 例如 Var 有利于 RMSE，relVar 有利于 relMSE

Limitations and Future Work

  • limitations
    • undersampling of small details（AS 普遍问题）
    • 没有考虑 bias
  • future
    • 使用其他的 NN 架构
    • randomized-QMC（quasi-Monte Carlo）
    • Temporal denoising
  • MC-SURE 可以使用上面定义的 \((\mathbf{J}_f(\mathbf{x}) \mathbf{v})_i \mathbf{v}_i\) 估计 SURE 的中间项，能够优化 SURE
    • 但是根据我们分析，使用 Var 引导 AS 比 Error 更好；认为不影响我们结论
    • 【没有做实验】