(论文)[2018-EGSR] Deep Adaptive Sampling for Low Sample Count Rendering

Posted on Edited on In Views:
联合优化适应性采样+降噪；第一次在适应性采样中引入神经网络（UNet 架构）；解决了两个训练问题（renderer 梯度传播、迭代过程中需要渲染很多适应性采样的图片）；开销约 10ms（GTX 1080Ti）

DASR

  • Deep Adaptive Sampling for Low Sample Count Rendering
  • University of California, San Diego
    • Alexandr Kuznetsov、Nima Khademi Kalantari、Ravi Ramamoorthi
    • 主页

摘要

  • 第一次训练了一个 sample map 用于 adaptive sampling（AS）【第一次在 AS 引入 NN】
    • 1spp 正常分配（用于估计 sample map），3spp 用于 AS（根据 sample map）
    • 联合优化 sampling map estimator、denoiser
    • end-to-end 训练，训练集上 denoised、GT 之间的 loss

  • 低样本下，传统 AS 失效（统计量不够）
  • 提出了高效的传播 renderder 梯度的地方
  • 效果：和 6spp + denoiser 效果差不多

Introduction

  • Monte Carlo (MC) path tracing
    • 实时 PT：低 spp
  • adaptive sampling
    • 均匀采样大量光线，计算一些量，用于计算 sample map
      • variance、coherence maps、frequency content
    • 问题
      • 需要大量样本
      • 将 adaptive sampling 和 reconstruction 视作独立阶段
    • 低样本失效：因此现在后处理方法都是使用均匀采样的结果作为输入
  • 贡献
    • 第一次在 AS 引入 NN
    • 迭代训练，提出了一种 AS 放置样本的方式
    • 计算 renderer 的梯度

Previous work

  • survey：[EG-2015] Recent advances in adaptive sampling and reconstruction for monte carlo rendering
  • joint adaptive sampling and reconstruction
    • use no-reference error estimation metrics
    • 计算 the bias and variance of a Gaussian , nonlocal means, local linear regression, and polynomial filters，利用 error 在多个阶段去分配样本
    • 低样本仍然不行
  • 学习方法
    • distributes the samples based on the summation of filter weights
    • NN 估计参数：the parameters of a cross-bilateral or cross non-local means filter

Method

Sampling Map Estimator

  • CNN
  • 11 通道 => 1 通道
    • RGB：noisy image、textures
    • shading normal、depth、direct illumination visibility
  • 归一化：网络输出 \(x(p)\)
    • 我们的例子中：\(n=3\)

\[ s(p)=\mathrm{round}\left(\frac{M}{\sum_{j=1}^{M}e^{x(j)}}\times e^{x(p)}\times n\right) \]

  • Sampling Map Estimator 和 Denoiser 都使用相同的 UNet
    • max pooling：2x2
    • 针对单张图片：不需要 recurrent 模块

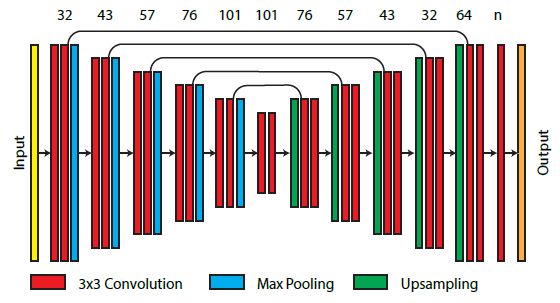
Denoiser

  • 11 => 3
  • 之前的工作（UNet 参考）
    • separate the texture from illumination：做不了 distributed effects（景深、动态模糊等）
    • 我们直接预测 => 可以做

Training

  • 两个问题
    • 需要迭代很多轮，每轮都需要渲染图片
    • renderer 如何反传梯度

Render Simulator

  • 预先渲染：\(I_{2^{0}},I_{2^{1}},\cdots,I_{2^{k}}\) spp 的图片（\(2^{k}=1024\)）
    • 这样可以拼出：\(1\sim2047\) spp 的图片
  • naive 策略：渲染很多 1 spp 的图片
  • 我们的策略更好，更省内存

Gradient of the Renderer

  • \(h\)：增加的样本数

\[ \frac{\partial I_{s}}{\partial s}=\frac{I_{s+h}-I_{s}}{h},\quad\text{where}\quad I_{s+h}=\frac{sI_{s}+hI_{h}}{s+h} \]

  • 噪声很大，\(N\) 次平均（需要预计算）

\[ {\frac{\partial I_{s}}{\partial s}}=\sum_{i=1}^{N}{\frac{I_{s+h}^{i}-I_{s}}{h\,N}},\quad\text{where} \quad I_{s+h}^{i}={\frac{sI_{s}+hI_h^i}{s+h}} \]

  • 简化（想去掉预计算）
    • 上面的式子，右边代入左边化简

\[ \frac{\partial I_{s}}{\partial s}=\frac{\sum_{i=1}^{N}\left(I_{h}^{i}/N\right)-I_{s}}{s+h} \]

  • \(N\to\infty\)：GT \(I_{\infty}\)

\[ \frac{\partial I_{s}}{\partial s}=\frac{I_{\infty}-I_{s}}{s+h} \]

  • \(h\to0\)：虽然不现实（对应不渲染图片，\(I_{\infty}\) 的推导不成立了），但是符合直觉（\(s\) 越大，边际效益越小）
    • 用于梯度计算及反传

\[ \frac{\partial I_{s}}{\partial s}=\frac{I_{\infty}-I_{s}}{s} \]

Implementation Details

  • https://cseweb.ucsd.edu/~viscomp/projects/dasr/
  • 数据集
    • 训练：700 组数据（来自 50 个场景，渲染 2 - 30 个视角）
      • GT：>1024spp
    • 有 distributed effect
      • depth of field, glossy reflections, motion blur, and global illumination
    • 测试：60 个测试场景【泛化性】
  • 网络输入
    • color、depth：范围大，\(\log(1+x)\)
    • 其他：标准归一化
  • 训练细节：3 stage
    • stage 1：训练 denoiser network【前面部分直接不管了】
      • 随机生成 sample map，为了保证 smooth，先低分辨率采样，然后 8x upscale
    • stage 2：只训练 sampling map network【两个网络都要，但是只更新第一个】
    • stage 3：一起 fine-tune（交替训练 sample、denoiser，一次迭代只训一个）
  • 输入：break down to 512x512
  • 训练
    • Adam，lr=1e-4
    • mini-batches of size 6
    • epoch：25000, 5000, and 40000 iterations
  • Loss：spatial and gradient
    • \(\mathcal{L}=0.5\mathcal{L}_{s}+0.5\mathcal{L}_{g}\)
    • spatial：rel L1，\(\epsilon=0.01\)
    • gradient：保证边界锐利
    • 范围太大：\(c=\log(1+\tilde{c})\)

\[ \mathcal{L}_{s}(\hat{c},c)=\frac{\left\Vert\hat{c}-c\right\Vert_{1}}{\left|c\right|+\epsilon} \]

\[ \mathcal{L}_{g}(\hat{c},c)=\frac{\left\Vert g(\hat{c})-g(c)\right\Vert_{1}}{\left|g(c)\right|+\epsilon} \]

Result

  • PyTorch 实现
  • 对比算法：需要统计量，4x4 patch 计算
    • 论文中说，其他 AS 算法效果很差（1spp 统计量太不准了）
  • 结果分析
    • 容易降噪的地方，我们算法分配光线少；难算、难降噪的地方分配多
  • 时间开销：GTX 1080 Ti GPU
    • 一共 10 ms（5+5）
  • future work
    • 低 spp 任务：investigate the possibility of performing joint sampling and denoising at multiple scales to be able to generate high quality results at the rates lower than 1 spp
    • 多 spp 任务