(论文)[2020-EGSR] Deep Kernel Density Estimation for Photon Mapping
Deep Photon Mapping
- Shilin Zhu、Zexiang Xu、Henrik Wann Jensen、Hao Su、Ravi Ramamoorthi
- University of California, San Diego、Luxion

- 摘要
- first deep learning-based method for particle based rendering
- 关注点:photon density estimation(和之前方法正交)
- 只需要 very sparse photons 就能实现 complex diffuse-specular interactions
Introduction
- PM 的工作很少关注:low-sample reconstruction
- 之前 PM:通过控制 kernel bandwidths or shapes 优化
kernel
- kernel function 比较简单:traditional kernel functions (like a uniform or cone kernel)
- 通用神经网络:训练
- 500 procedurally generated scenes with complex shapes and materials
- 512x512 分辨率
- sample surface points on diffuse surfaces
- 每一个 surface point 作为一个数据点
- GT 使用 PPM 算法得到
- 算法流程
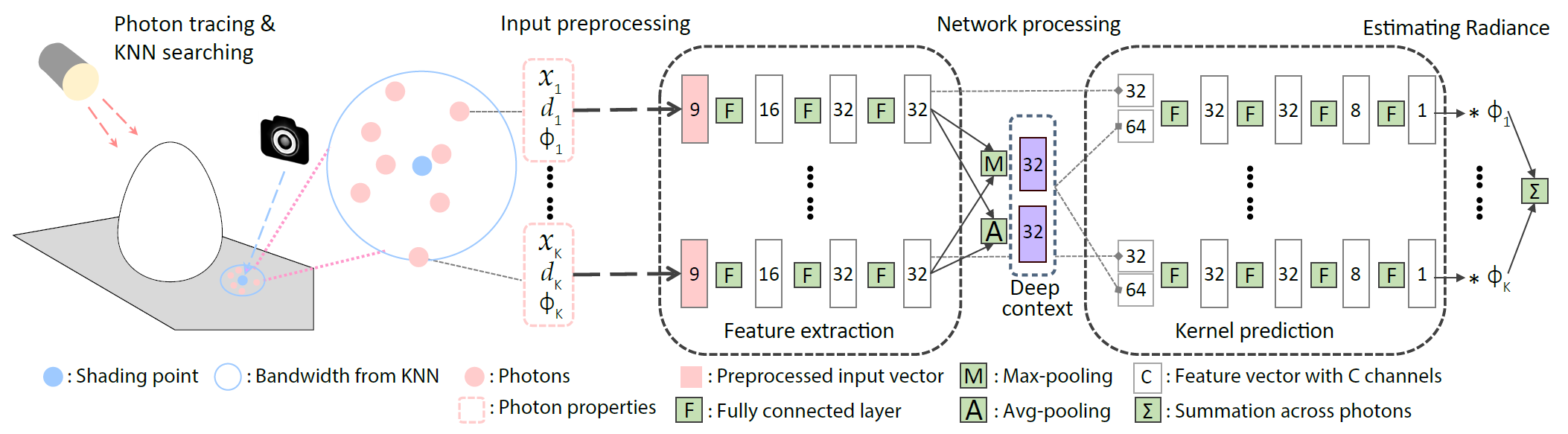
Related Work
- MCPT、BDPT、MLT
- Monte Carlo denoising
- 先验:prior theoretical knowledge
- 后验:assumptions about the image signal
- deep learning:...
- Photon density estimation
- PM
- blurred, less noticeable artifacts
- 一致的:光子趋于无穷,半径趋于 0
- 改进:无穷光子(显存瓶颈)、adaptive kernel bandwidth、anisotropic kernel shapes
- PM
Density estimation
- general formulation
- \(r\):bandwidth
- \(\tau_i\):贡献(BRDF x photon
energy)
- 我们只做 diffuse 表面的估计:\(\tau_i=\dfrac{\rho}{\pi}\times\phi\)
\[ L(x,\omega)\approx\frac{1}{N}\sum_{i=1}^{N}k_{r}(x,x_{i})\tau_{i} \]
- traditional \(k_r\)
- uniform function:\(1\Big/(\pi r^2)\)
- 关于距离的函数:\(f(\Vert{x-x_i}\Vert)\)
Learning to compute photon density

- 流程
- 给定 shading point,找到 K 的最近的 photon(自适应确定 bandwidth \(r\))
- photon 的属性(位置 \(x_i\)、方向 \(d_i\)、贡献 \(\phi_i\))输入网络,输出权重
- \(\Phi_{r,i}\):kernel weight
\[ L(x)\approx\frac{\rho}{N\pi r^{2}}\sum_{i=1}^{K}\Phi_{r,i}\left(x,\{x_{i}\},\{d_{i}\},\{\phi_{i}\}\right)\phi_{i} \]
Input pre-processing
- for better generalizability and performance
- \(\tau_i\)
动态范围十分大,网络处理不好,因此加上转换:\([0,+\infty]\to[0,1]\)
- 线性变换到 \([-1,1]\) 之后作为网络输入
- 便于训练
\[ t_{a}(u)=\frac{\log(u+a)-\log(a)}{\log(u+a)-\log(a)+1} \]
- \(x_i,d_i\)
- 先转化到 local coordinate frame(通过着色点的位置、法向 + tangent plane 上随机采样两个方向得到)
- 泛化性
- bandwidth \(r\) 随着 K 个最近的
photon 的选择而确定
- 因此 \(r\) 的范围也大
- 参考之前的 bandwidth normalization 工作,进行如下操作,体现在公式中
- 将 local position \(\Big/r\):将所有的光子归一化到单位圆中
- 将最终的贡献 \(\Big/ r^2\)
- 这样处理之后,网络和 \(r\) 无关(对 \(r\) 泛化)
- 所有的输入都归一化到 \([-1,1]\) 之间
- 预处理输入的效果
- makes our network translation-, rotation-, and scale- invariant to diverse photon distributions, leading to good generalization across different scenes and different numbers of emitted photons.
Network architecture
- 输入的 K 个点是顺序无关的:参考 PointNet
设计(任意输入个数、输入顺序无关)
- feature extractor、kernel predictor 所有 photon 独立过
- 相关性通过 Deep context 部分建模

- feature extractor:将输入转化为 32 通道的 feature vector
- This vector represents the local photon statistics in a learned non-linearly transformed space
- Deep Context:建模相关性
- Maxpooling、AvgPooling
- kernel predictor:将 across-photon context、the per-photon features 转化为一个权重系数
Training details
Data generation
- 关注 local photon distribution(学习 proper data priors)
- 程序化的随机生成场景
- 随机生成随机大小的 shapes + bump maps(1-16 个)
- 将 shapes 放到 box 里面(近似 grid 分布摆放)
- 随机放置多个面光源:随机位置、随机旋转

- 512x512 分辨率,第一个击中的 diffuse 作为 target shading point
- PPM 计算 GT(1B photon paths)
- 训练数据集
- 500 场景
- 每个场景
- 保存 10 million photon paths and a 512x512 multi-channel image
- GT radiance、shading points 的必要信息
- 测试:使用和训练数据集不同(泛化性)
Loss function
- 动态范围太大:tone-mapping 后 L2 loss
- \(\mu\)-law:\(p_{\mu}(v)=\dfrac{\log(1+\mu
v)}{\log(1+\mu)}\)
- \(\mu=5000\)
Training parameters
- 随机
- K:100-800
- photons:0.3M- 4M
- Adam:6000 epochs、initial lr=1e-4、batch size=2000
Experiments
- Ablation study
- 网络有效性
- 对比 baseline:直接从 deep context 输出 irradiance
- 网络有效性
- Evaluation scenes and photon generation
- 测试场景:常见的 6 个焦散场景
- 使用面光源:不欺负 PT
- 细节
- 0.1s 生成光子:0.8M(~5 per pixel)
- 只保存含有 light-specular(LS) 的 paths(记作 \(M\) 条)
- 泛化性测试:1.0s 生成光子(对光子数目泛化)
- Combining MC denoising and deep photon mapping
- 结合 MC denoising(Optix)
- 去掉 LS paths,PT+降噪很有效(100spp);加上则不行(1000spp效果都不行)
- Parameters of our network and comparison methods
- 对 K 泛化很难,因此网络训练和测试,使用相同的 K
- 大网络效果好,但是耗时长
- PPM 对于初始半径设置、每次迭代光子数敏感
- 因此对比的时候,在 30 个配置下选最好的作为结果(最低的 RMSE)
- 10 radius and 3 photon counts per iteration
- 因此对比的时候,在 30 个配置下选最好的作为结果(最低的 RMSE)
- Quantitative and qualitative evaluation
- K 越大,效果越好
- PM:K 大了可能会糊(我们方法学到了分布,因此不糊)
- APPM:动态调整 bandwidth;小样本时我们更好
- Time
- NVIDIA 1080 Ti GPU
- Kd-Trees 做范围查询
- 右边:网络推理时间只和 K 相关(相同 spp)

- Temporal consistency:不太行
- Progressive density estimation
- 支持动态的 K(我们方法原生支持,但是如何变化是个问题)