(论文)[2022-SIGC] Neural Shadow Mapping

Posted on Edited on In Views:
神经阴影贴图；通过将光源大小编码进输入，能够实现一个网络同时输出软硬阴影；类似 noise2noise 的学习，设计 loss，提高了时间上的稳定性；通过简化 UNet 架构实现实时性（<5ms）；针对不同场景的最大半影大小，可以使用不同深度的网络；通过微扰，挑选出对结果影响最大的 4 个通道作为网络输入（减少了输入的通道数，原来 13）

Neural Shadow Mapping

  • We propose a machine learning-based method that generates high quality hard and soft shadows for dynamic objects in real time.
  • 优势
    • 不需要光追硬件
    • <6ms
    • <1.5MB 内存
    • 低端 GPU 可行
  • 光栅化的硬阴影 => temporally-stable hard and soft shadows
  • 输入包含光源大小：因此可以在训好的网络中生成软/硬阴影

相关工作

  • 现代阴影算法：combine many cascaded maps
  • Filtering-based
    • PCF、PCSS
    • statistical proxies：VSM、Convolution Shadow Maps
    • Moment shadow maps（sota）
  • Screen-space methods：使用 G-buffers
  • Ray tracing hardware

OVERVIEW

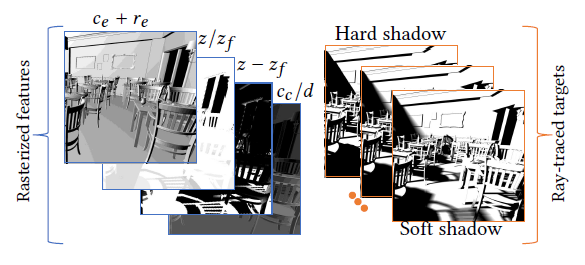
  • 训练：有监督学习
    • 输入：shadow pass + G-Buffer pass 获取到的 buffer
    • GT：ray traced shadow
  • 网络（优化前）：UNet（>25MBs、>100ms）
  • 简单：即插即用
  • 训练输入：光栅化不 MSAA（希望网络去学）
    • view-space depth \(d\) and normal \(\mathbf{n}\)
    • emitter-to-occluder depth \(z\) and emitter-space normal \(\mathbf{n_e}\)
    • pixel-to-emitter distance \(z_f\) , the emitter radius (size) \(r_e\) for spherical sources
      • \(r_e\) 控制阴影软硬程度：\(0-4\)（点光源 - 半径为 50cm 的球）
    • dot products \(\{c_e , c_c \}\) of \(\mathrm{n}\) with the emitter direction and \(\mathrm{n}\) with the viewing direction
  • GT
    • PT + mild Gaussian filter
    • 8x multi-sample anti-alising (MSAA)

Feature selection

  • feature selection network 效率低，而且带宽不友好，于是我们自己选
    • 输入有 15 个通道：\(U=\left\{d,{\bf n},z,{\bf n_e},z_{f},c_e,c_{c}\right\}+\left\{z-z_{f},z_{f},z_{f},c_{c}/d,{\bf n}\cdot{\bf n_e}\right\}\)
  • 定义 sensitivity：给某个输入通道的纹理进行扰动，看对网络输出结果的影响
  • Absolute sensitivity \(S_i\)

\[ S_i =\mathbb{E}\left[\frac{(\phi(f_{i}+\epsilon_{i})-\phi(f_{i}))}{0.1\sigma_{i}}\right], \epsilon_{i}\sim \mathcal{N}(0,0.1\sigma_{i}) \]

  • relative sensitivity：\(s_i=S_i/\sum S_i\)
    • across different training instances（一个场景的多个实例）
  • 选择过程：一开始使用所有通道，然后拒绝 \(s_i\) 最低的，重复直到左右的 \(s_i>1.5\%\)
  • 最终结果：不同场景的 relative sensitivity

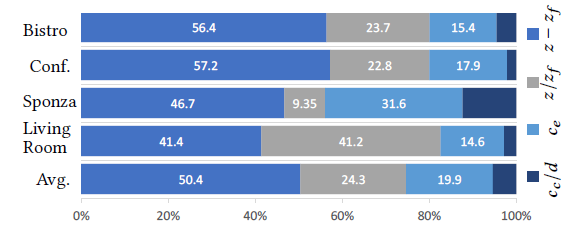
  • 这样节省了 2.5ms

Loss function and temporal stability

  • 两个要求
    • 能够处理硬阴影边界和几何（AA 后处理）
    • 训练和推理都不需要历史的 buffer
  • 节省带宽 + 容易嵌入 tiled renderer

要求 1

  • a weighted combination of per-pixel difference and VGG-19 perceptual loss
  • VGG 能起到抗锯齿作用

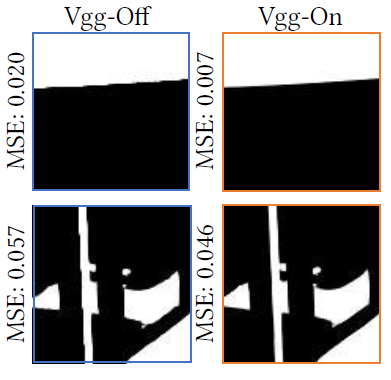
要求 2

  • 时间上的不稳定性来源：shadow-map aliasing
    • shadow map texels do not align one-to-one with screen pixels
    • 小的移动可能会导致深度对比的时候有大的变化（尤其是阴影边界）
  • noise2noise 论文启发：训练引入噪声（perturbation 扰动）
  • 下面操作：在扰动的情况下，依然能得到变化不大的结果
  • 每一个迭代轮，对 camera and emitter position 进行扰动
    • 正比于 the distance from the scene and size of emitter
  • 每次扰动，选择所有输入进行训练，但是只选择其中的一个状态作为真值
    • 输入状态不同，但是 GT 相同
    • 只有一个样本反传梯度，例如下面的红色的 \({\color{red}x_{0}}\)
      • \(x_i\)：网络输出，\(\tilde{x}\)：GT
    • \(p=3,\alpha=0.9\)

\[ \mathcal{L}=L({\color{red}x_{0}},\tilde{x})+\sum_{i=1}^{p}L({\color{red}x_{0}},x_{i}) \]

\[ {\cal L}(y,\tilde{y})\,=\,\alpha\cdot|y-\tilde{y}|\,+\,(1-\alpha)\cdot \text{VGG19}(y,\tilde{y}) \]

  • 扰动：时间稳定性变好，空间模糊变多

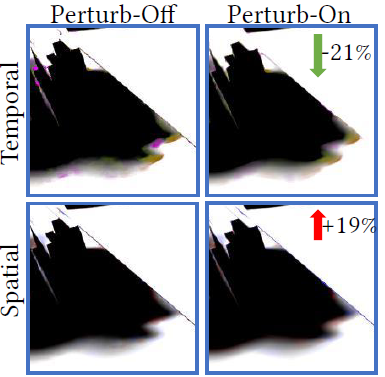
Temporal stability measurement

  • 之前的工作一起评估 spatio-temporal，因此不太好（因为我们牺牲了 spatial 想取得更好的 temporal）
  • 构造

\[ E=\frac{1}{P}\sum_{p,t}\left\{\exp(\alpha D_{t}(p))-1\right\} \]

\[ D_{t}(p)\ =\ |I_{t}(p)-I_{t-1}(m(p))| \]

  • \(m(p)\)：应用 motion vector 到上一帧的结果
  • \(P\)：所有像素
  • \(\alpha=3\)：penalty for large changes
  • We reject pixels that fail depth and normal comparison with its reprojection.
  • 用这个指标去评价 temporal 的稳定性：效果比 TAA 好，而且 -1.3ms
  • 这个指标是用于评价，而不是训练

Network architecture and optimizations

  • 原版 UNet 太慢：>100ms
  • 压缩

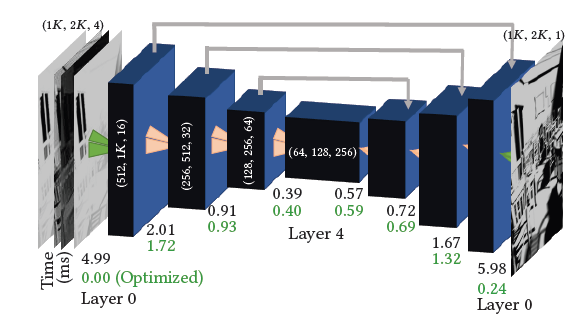
  • 每一层：composed of one 3x3 convolution and one 1x1 convolution layer
  • 上采样：bi-linear interpolation
    • 快，不是原来的 transpose convolutions
  • skip connections：使用算术和，而不是 feature concatenation
  • 结果：25MB -> 2.5MB，28ms
  • 半精度存储：1.5 MB，17ms
  • 其他不提高 temporal 的修改
    • Average-pool instead of Max-pool：更加平滑
    • 去除第一层的 skip-connection：输入 depth 存在锯齿
  • UNet 内到外的时间开销（通道/2，分辨率x4），由于存在 cache miss，时间不止 x2
  • 其他优化：优化第一层（开销最大）
    • naive：套一个降采样，最后上采样（会丢失细节）
    • 我们：2x2 合成一个
      • 输入： \(h\times w\times ch\to h/2\times w/2\times 4ch\)
      • decoder 端逆向操作：前4个通道双线性插值，然后再把后12个通道累加到对应位置（填补细节）
    • 此时优化到 5.8ms

Network depth optimizations

  • 上面的优化都是通用的，下面的优化是 scene-specific 的
  • 浅层网络：快（训练、推理）
  • 我们先根据场景配置估计出最大的半影大小，然后根据这个值调整网络深度
  • 假设：spherical occluder（或者 bounding sphere）
  • 每个像素：认为半影大小 \(=x_a+x_b\)

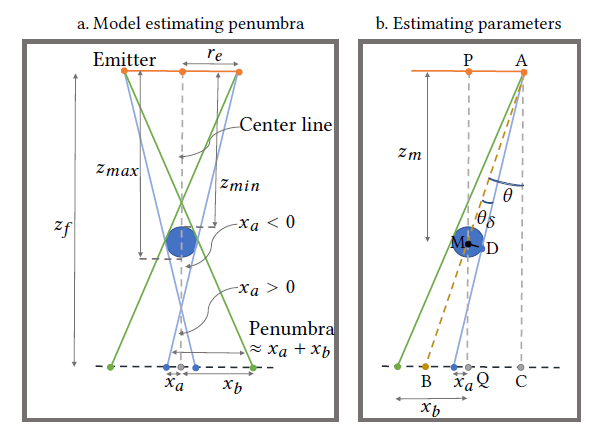\[ \{x_a,x_b\}=z_f\tan(\theta\pm\theta_\delta)-r_e \]

  • 取所有像素所有帧的半影大小，95%分位数作为我们的判定值（\(x\) 个像素）
  • 卷积让分辨率减半，感受野（effective receptive field）随层数变化：\(\times2^l\)
    • \(3\times3\) kernel：\(l=\log_2(p_w/3)\)
  • 验证：3个网络层数：3、5、7，MSE 如下

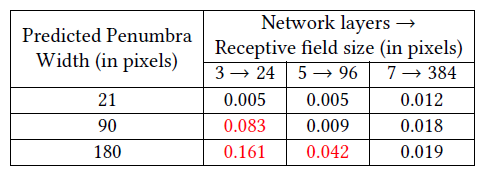
结果

  • 训练可以泛化：在一个场景中训完之后，可以在场景中加入没有见过的物体
  • 对比算法：MSM、PCSS、GPU ray-tracing+denoise（5spp+SVGF）
  • 分辨率：1kx2k
  • 测试：AMD 5600X CPU and Nvidia 2080Ti GPU
  • Each scene is trained on \(\le\) 400 images of resolution 2kx1k on a cluster for roughly 16 hours (75 training epochs)

limitation

  • 常见屏幕空间问题：unavailability of layered depth information
    • camera-space 和 screen space 像素不是一一对应的
  • shading points 和 occluders 之间的距离不能准确计算