(论文)[2024-SIG-C] Neural Bounding

Posted on Edited on In Views:
提出了一种新的求 bounding 的方式，引入非对称的 loss 去限制 FN=0，但是训练很慢，推理也比较慢，但是 bounding 更加紧致，不能泛化（单物体训练）

Neural Bounding

贡献

  • 提出了一种新的求 bounding 的方式，引入非对称的 loss 去限制 FN=0，但是训练很慢，推理也比较慢，但是 bounding 更加紧致，不能泛化（单物体训练）
  • 感觉它把非对称 loss 当作最大贡献了
  • 引入网络也算创新点吧
  • 不太懂为啥能发出来，感觉乱七八糟的。。。

Abstract

  • Bounding Volume 可以转化为一个分类问题：这个空间是否被占据
  • 要求
    • false positive（FP）尽可能少：效率高
    • false negative（FN）不能出现：保证正确性
  • 示例：box (a), ellipsoid (b), k-oriented planes (c), common neural networks (d) and a neural network trained using our approach (e)

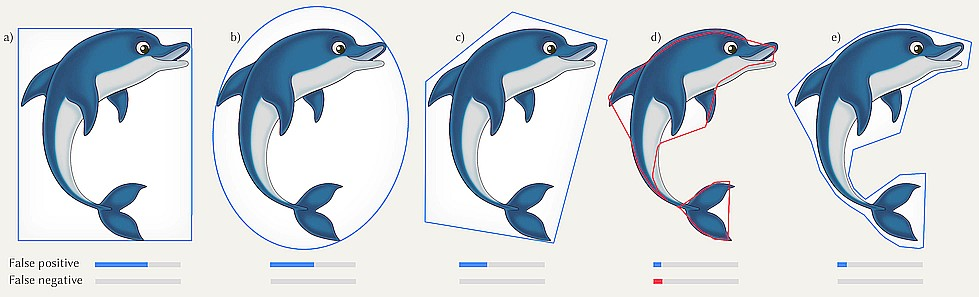
Introduction

  • BVH 的 trade offs
    • 和 bounding primitive 求交的计算代价
    • 和原始 primitive 求教的计算代价
    • bounding primitive 的 FP rate
  • 理想的 bounding 策略：FP rate 低、bounding primitive 的计算代价低
  • 经典策略：spheres, boxes, oriented boxes, k discretely-oriented polytopes (k-DOPs)
    • result in poor FP rates as they remain convex
  • 本文，利用 NN 实现
    • high-dimensional, non-linear, concave bounding with a combination of simplicity, flexibility and testing speed
  • 挑战：如何让 NN 的 FN rate 为 0
  • 两种策略
    • 先找 bounding，然后使用 NN 近似
    • 使用 NN 去估计复杂几何体，然后进行保守估计
  • 为了实用：网络需要 small and simple（快）
  • 应用
    • two, three and 4D point queries, 2D and 3D range queries as well as queries of dynamic scenes
    • 传统方法的优化

previous work

  • k-DOPs、AABB 等
  • BVH
  • NN
    • Neural intersection functions：不是保守的，静态场景
    • Occupancy Networks（CVPR2019）
  • 其他领域
    • Neural Polytopes
    • Neural collision detection for deformable objects
  • 非对称 loss

our approach

Method

  • 学习一个 indicator function \(f(\mathrm{x})\in\mathbb{R}^{n}\to\{0,1\}\)
    • 1：inside、on the surface
    • 0：else
  • query function \(g(\mathrm{r})\in\mathbb{R}^{m}\to\{0,1\}\)，region \(\mathrm{r}\)
    • 1：存在一个 \(\mathrm{r}\) 中的点 \(\mathrm{x}\) 满足 \(f(\mathrm{x})=1\)
    • 0：else
    • 点查询：\(g=f\)
    • 范围查询：\(\mathrm{r}\) 是区域的一个参数化（例如 AABB 的两个端点）
  • \(h_{\theta}(\mathrm{r})\in\mathbb{R}^{m}\to\{0,1\}\)
    • 可学习的参数 \(\theta\)
    • 当 \(g=1\) 的时候，严格为 1；其他没关系（允许 FP）
  • loss \(\mathcal{L}\)
    • \(\alpha\to\infty\) ：不允许 FN
    • \(\beta=1\)：FP 越少越好

\[ \mathcal{L}(\theta)=\int c(\mathbf{r})\mathrm d\mathbf{r} \]

\[ c(\mathbf{r})= \begin{cases} 0& \text{if}\ g(\mathbf{r})=0\ \text{and}\ h_\theta(\mathbf{r})=0,&\text{TN}\\ \alpha& \text{if}\ g(\mathbf{r})=1\ \text{and}\ h_\theta(\mathbf{r})=0,&\text{FN}\\ \beta& \text{if}\ g(\mathbf{r})=0\ \text{and}\ h_\theta(\mathbf{r})=1,&\text{FP}\\ 0& \text{if}\ g(\mathbf{r})=1\ \text{and}\ h_\theta(\mathbf{r})=1,&\text{TP} \end{cases} \]

  • \(c\) 不连续，只有在 surface 边界才有导数
  • 无穷无法处理
  • \(\mathcal{L}\) 的修改
    • \(\alpha(t),\beta(t)\) 替换 \(\alpha,\beta\)：极限意义上 FN 的代价还是 \(\infty\)
      • \(t\uparrow\Longrightarrow\alpha\uparrow,\beta\downarrow\)（补充材料是不是说反了，和前面这里的逻辑反一下）
        • \(\alpha\) 变化就够了（引入了不对称性），\(\beta\) 反向变化是为了加速训练
        • 代码里面其实只修改了降低了 \(\beta\)
      • FN：\(\hat{y}=0,y=1\)，loss 体现在 \(\alpha\) 项
  • weighted binary cross-entropy（indicator function）

\[ \hat{\mathcal{L}}(\theta)=-\mathbb{E}_i[\alpha(t)\cdot y_i\log(\hat{y}_{i,\theta})+\beta(t)\cdot(1-y_i)\log(1-\hat{y}_{i,\theta})] \]

\[ \hat{y}_{\theta}=h_{\theta}(\mathrm{x}),y=f(\mathrm{x}) \]

  • 计算流程如下（region query function）

Neural Bounding Hierarchies

  • 树结构需要用户构建：NN 只在每个节点上进行
  • 有点无语的。。。。。。

Neural Early-out

  • bounding hierarchies 的好处：不像其他 NN 一样，可以提前结束测试（节省计算时间）
    • 加入 additional conservative and negated immediate loss
  • 举例：MLP（\(A_1\) 层、\(\text{nl}\) 非线性激活层、\(A_2\) 层）
  • 常规 loss
    • bce：binary cross-entropy
    • \((\cdot\mid1)\)：the bias-trick（offset，\(Ax+b\) 中的 \(b\)）

\[ \mathcal{L}_{\text{Late}}(\mathbf{r})=\mathrm{bce}(h_{\theta}{}^{\text{Late}}(\mathbf{r}),g(\mathbf{r})) \]

\[ h_{\theta}^{\text{Late}}(\mathbf{r})=\mathrm{nl}\left(\mathrm{A}_{2}\times(\mathrm{nl}(\mathrm{A}_{1}\times(\mathrm{r}\mid1))\mid1)\right) \]

  • 更新后的 loss
    • 加入\(A_3\) 层（小网络）
    • \(h_{\theta}^{\text{Early}}(\mathbf{r})\) 和 \(h_{\theta}^{\text{Late}}(\mathbf{r})\) 相反

\[ \mathcal{L}_{\text{Early}}(\mathbf{r})=\mathcal{L}_{\text{Late}}(\mathbf{r})+\mathrm{bce}(h_{\theta}^{\text{Early}}(\mathbf{r}),1-g(\mathbf{r})) \]

\[ h_{\theta}^{\text{Early}}(\mathbf{r})=\text{nl}(\mathrm{A}_{3}\times(\mathrm{r}\mid1)) \]

  • 测试的时候，先运行 Early NN
    • 如果输出 negative，那么就认为是 negative 不再执行
      • 输出 negative 应该指的是 \(1-h_{\theta}^{\text{Early}}(\mathbf{r})\) 是不相交？是这个意思吗？
    • 否则再执行 Late NN，得到最终结果
  • Early 和上面的 loss 相比，是 inverse conservative
    • 不太明白为什么有用？感觉就是估计了一个 Late 的 \(1-\text{Late}\)，效果应该和前面类似
    • 可能是小网络，更加快速近似？这个保守性为啥会更好？
  • 在 NN 很大的时候，这样的 Early 技术，可以有多层，帮助节省时间
  • 点查询快 1 倍，范围查询快 25%
  • 代码中没有这个部分，不太懂具体原理

Implementation

  • 我们的方法与具体应用的实现无关，但是有些结构会影响我们的 bounding 的 tightness

Architecture

  • MLP：支持任意维度的查询（不同的查询方式是需要单独训练网络的）
  • 中间层激活函数：Sinusoidal（正弦）
  • 输入：采样得到的 mD query
  • 输出：sigmoid 归一化到 \((0,1)\)，然后四舍五入到 \(\{0,1\}\)
  • 有 positional encoding
    • 没有 residual-、skip-connections、Batch-Normalization（实验效果不好，可能是因为网络比较浅）
  • PyTorch

Training

  • Adam（lr=\(\text{1e-3}\)）
  • batch size of 200,000
  • early-stop the training as soon as FN = 0（6 次迭代左右）
  • 训练时间：20 to 60 minutes on a modern workstation
    • an RTX3090 GPU and Intel i9-12900K CPU（真的吗？不太信）
  • 泛化
    • 针对单物体训练，不泛化
    • generalization of bounds across the hypercube of space, time, query type, and combinations thereof.（查询种类泛化）

Evaluation

  • 对比算法
    • AABox、OBox
    • Sphere
    • AAElli and OElli
    • kDOP（\(k=4m\)）
  • BVH：只用于判断是否被包围（shadow ray 比较像）
  • 论文算法
    • OurNN、OurNNEarly
    • OurReLUField（neural grid method）：训练快，但是低维度
    • OurkDOP：用于 kDOP 的优化
  • 对比算法：NN
    • OccNet（Occupancy Networks，对称 loss，\(\alpha=\beta=1\)）
    • 只比质性结果，OccNet 不保证 FN = 0
  • 可能也会出错，论文说是数值问题
    • 结果：find fewer than 1 FN in 100 million queries on hidden test sets
    • 训练越多结果越好

Tasks

  • task
    • 查询维度：\(n=2,3,4\)
    • 查询方式：points, rays, planes and boxes
  • Indicators
    • 2d 数据集（9 张图片）， 32x32 的图片（黑白 2 色），真的离谱这学半小时都还学不出来
    • 3d 数据集（9 个体素），binvox 格式（在线查看），32x32x32
    • 4d 数据集（3 个），3d 模型围绕中心旋转，10x32x32x32
      • 对于传统方法，例如 AABB 来说，旋转比平移更容易（平移会将其拉的更大，FP 会更多）
      • 感觉一样吧，大家都简单了
bunny chair dragon1 dragon2 house lucy star1 star2 teapot
star1

  • Query types：point-, ray-, plane- and box-queries
    • ray：起点和方向
    • planes：normal + 面上的一个点（Aliased Rays 的问题？）
    • boxes：最大最小的两个顶点
    • 询问：any()，有相交就是相交

Metrics

  • tightness、execution speed
  • tightness
    • MC 的方式计算 FP（越小说明越紧致）
    • FN 应该严格等于 0
  • execution speed
    • 10,000 independent runs with 10 million randomly sampled
    • 都是 pytorch 上实现，向量化并行，充分利用 GPU（感觉 3090 在睡觉）

Results

Quality

  • FP rate（tightness）

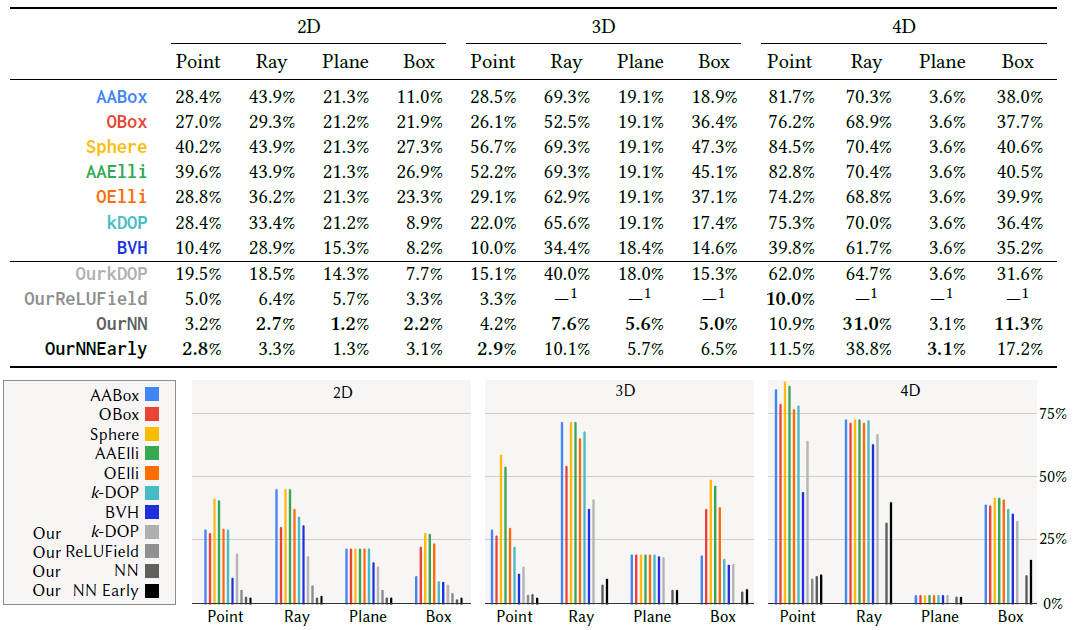
  • 论文效果很好，其次的是 BVH（呵呵呵）
  • 维度增加都变差了（问题变难了）
  • 随着 NN 的而复杂度增加，NN 的 bounding 会更加 tight
  • 能够通过互换 \(\alpha,\beta\) 实现
    • FP=0（\(\alpha,\beta\) 互换）：黄色 bound
    • FN=0（正常）：蓝色 bound

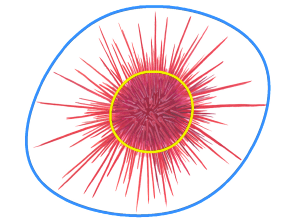
  • NN+BVH：父节点的 bound 不需要包含子节点的 bound

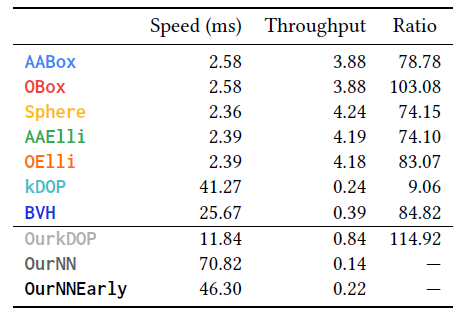
Speed

  • 慢一些，但是能和 kDOP 差不多
  • throughput：x billions tests per seconds
    • 这咋算的？
  • Ratio：下面解释

Discussion

  • 比传统方法慢，为啥还有应用价值？
    • tightness and scalability

tightness

  • \(t\)：精细几何求交开销
  • \(t_i\)：bounding 方法开销
  • \(p_i\)：FP 的概率（FP+TP=1）
  • \(N\) 次测试的计算开销如下：\(Nt_i+p_i\cdot N\cdot t\)
    • 或者这么理解，首先大家的 FN=0，所以范围 \(\mathrm{r}\) 都可以分为 3 个区域：\(A,B,C\)（并为全集）
    • \(A\) 区域返回没有相交，此时 FN=0，于是返回没有相交（额外开销 0）
    • \(B\) 区域为 FP 区域，此时需要进行精细求交（额外开销 \(N\cdot t\)）
    • \(C\) 区域为 TP 区域，此时大家都需要精细求交（额外开销 \(N\cdot t\)）
    • 此时总的开销为 \(Nt_i+B\cdot N\cdot t+C\cdot N\cdot t\)，最后一项相同，只需要比前两项
      • \(p_i=\dfrac{B}{A+B+C}\)
  • 对比不同方法，A 方法优于 B 的条件

\[ \begin{aligned} N\cdot t_{a}+Np_{a}\cdot t& <N\cdot t_{b}+Np_{b}\cdot t \\ t_{a}+p_{a}\cdot t& <t_b+p_b\cdot t \\ t_{a}+p_{a}\cdot t-p_{b}\cdot t& <t_{b} \\ p_{a}\cdot t-p_{b}\cdot t& <t_b-t_a \\ t(p_{a}-p_{b})& <t_b-t_a \\ \end{aligned} \]

\[ \begin{aligned} (p_{a}-p_{b})>0&\Longrightarrow t <(t_b-t_a)/(p_a-p_b) \\ (p_{a}-p_{b})<0&\Longrightarrow t>(t_{b}-t_{a})/(p_{a}-p_{b}) \end{aligned} \]

  • Ratio
    • \(a=\text{OurNN}\)，\(b\) 为对应行算法
    • 首先 \(p_a<p_b\)，因此只需要满足 \(t>\text{Ratio}\cdot t_b\)，那么 OurNN 就更优

  • 上面的 Ratio 很容易实现，因为一个节点中常常含有很多三角形（Millions）

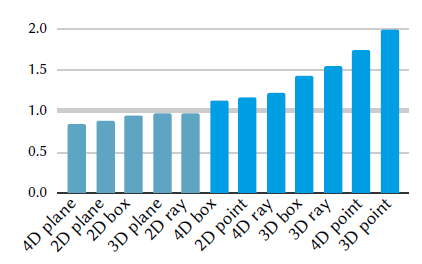
Early-out

  • runtime：OurNNEarlyOut/OurNN

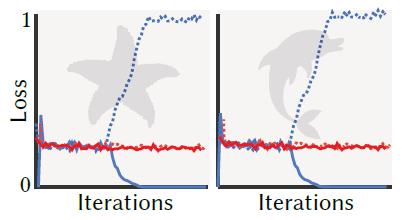
Convergence

  • 没太懂这一段想表达什么
  • 非对称 loss 的好处
    • 蓝色：我们方法；红色：一般方法
    • dot：FP；solid：FN
  • FN 变成 0 的代价是 FP 会增加
    • 所以 FN 变成 0，就结束训练？

scalability

  • 高维空间例子
  • 在一个训练好的 VAE 生成数字的模型中，10d 隐空间 + 2d像素位置，让生成的数字加上 bounding

Limitations

  • 不能保证 no FNs
  • 不能在物体间泛化，trained per-object，训练慢
    • 加速训练：tinycudann、meta-learning
  • 运行速度也比较慢
  • sampling the indicator only works if object- and query-dimensions align
    • ？
  • 网络引入额外内存开销，比之前方法大很多