(论文)[2023-SIG] 3D Gaussian Splatting for Real-Time Radiance Field Rendering

Posted on Edited on In Views:
3D 高斯重建，第一个实现重建的实时渲染，训练速度和当时最快的 InstantNGP 差不多，出图质量和当时最好 Mip-NeRF360 的差不多。解决了两个问题，场景中很多地方是空的，快速的可微的渲染管线。

3DGS

  • 3D Gaussian Splatting for Real-Time Radiance Field Rendering
  • 作者
    • Bernhard Kerbl、Georgios Kopanas、George Drettakis（Inria, Université Côte d’Azur, France）
    • Thomas Leimkühler （Max-Planck-Institut für Informatik, Germany）
  • 项目主页

Abstract

  • 3DGS
    • 实时渲染
    • 效果和 sota（Mip-NeRF 360，2022）差不多
    • 训练时间和之前训练最快的算法差不多（InstantNGP，2022）（Plenoxels，2022）

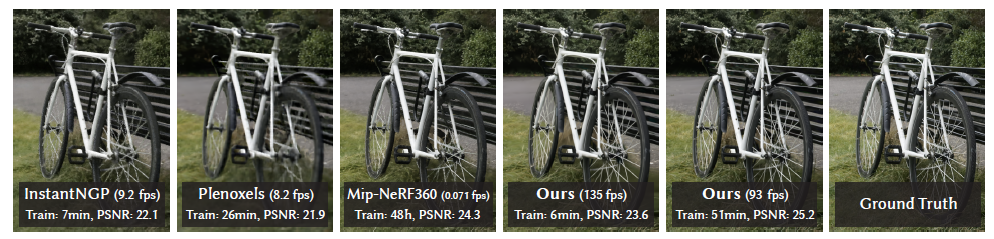
  • 关键：3D Gaussian scene representation coupled with a real-time differentiable renderer
  • 之前没有算法能实现 1080p 实时渲染（>30fps）
  • 3DGS 能实现的原因
    • 初始是场景中的稀疏点，使用 3D Gaussian 表示场景，避免了场景中空白区域的无用计算
    • 对 3D Gaussian 的优化、密度控制
    • fast visibility-aware rendering algorithm（训练渲染都快了）

Introduction

3 个组件

  • 引入 3D Gaussian 作为场景的表示
    • 输入和 NeRF 类似：相机位姿（SfM 得到）
    • 利用稀疏点云（可以伴随 SfM 生成）初始化 3D Gaussian 的位置
    • 和其他方法不同，我们只需要 SfM 的点，不需要多视角的数据（Multi-View Stereo，MVS）
    • 在 NeRF-synthetic dataset 中，随机初始化效果也很好
    • 3D Gaussian 的好处：可微的体表示+快速光栅化（标准 \(\alpha\) 混合）
  • 3D Gaussian 属性、数量的优化
  • 实时的渲染算法（快速 GPU 排序）

Related Work

传统重建

  • Traditional Scene Reconstruction and Rendering
  • novel-view synthesis
    • densely sampled
    • unstructured capture
    • Structure-from-Motion (SfM)：在相机位姿矫正中生成稀疏点云
  • re-project and blend the input images into the novel view camera and use the geometry to guide this re-projection
  • 问题：当出现如下区域的时候，重建效果不好
    • MVS 未重建的区域
    • MVS 生成不一致的 mesh

Neural Rendering and Radiance Fields

  • 早期工作使用 MVS-based geometry，效果一般
  • 体表示
    • Soft3D
    • 基于连续可微的密度场 + ray marching
    • NeRFs：引入重要性采样、位置编码
      • 后续：加速、提高质量
      • 加速
        • 使用空间数据结构存储特征
        • 不同输入编码：hash table、sparse voxel grid、SH 球谐函数
        • MLP 大小：space discretization、codebooks
      • 比较难处理空间大部分空白，很难有效表示

点渲染与辐射场

  • Point-Based Rendering and Radiance Fields
  • 可以有效渲染 disconnected and unstructured geometry samples（例如点云）
  • 早期点云渲染：存在 alias，最明显的就是不连续性
    • 用 API 实现固定大小的点渲染
    • GPU 上的软光栅
  • 一些开创性的工作，让点的大小超过一个像素（splatting）
    • circular or elliptic discs, ellipsoids, or surfels
  • 最近工作：differentiable point-based rendering techniques
    • 点上带特征，然后使用 CNN 渲染（CNN 引入时间上的不稳定性）
    • 需要 MVS 提供的几何，继承了 MVS 的问题
  • Point-based \(\alpha\)-blending and NeRF-style volumetric rendering 的 formulation
    • 样本的 density \(\sigma\)、transmission \(T\)、颜色 \(\mathrm{c}\)
    • 沿着光线，和上一个样本的距离 \(\delta\)

\[ C=\sum_{i=1}^NT_i(1-\exp(-\sigma_i\delta_i))\mathbf{c}_i\quad\text{with}\quad T_i=\exp\left(-\sum_{j=1}^{i-1}\sigma_j\delta_j\right) \]

\[ C=\sum_{i=1}^{N}T_{i}\alpha_{i}\mathbf{c}_{i},\quad \text{with}\quad\alpha_{i}=(1-\exp(-\sigma_{i}\delta_{i}))\ \text{and}\ T_{i}=\prod_{j=1}^{i-1}(1-\alpha_{i}). \]

  • neural point-based 方法
    • \(\mathcal{N}\) 个排序的点
    • \(\alpha\)：每一个 2D Gaussian 的协方差 \(\Sigma\) 乘上每个点学习到的不透明度
    • 和上面一样的模型，但是理论不同
      • NeRF 隐式表示连续空间（需要高代价的随机采样点）
      • 点是便是表示离散空间
    • 3DGS 使用的就是下面这个式子

\[ C=\sum_{i\in\mathcal{N}}c_i\alpha_i\prod_{j=1}^{i-1}(1-\alpha_j) \]

  • fast sphere rasterization：启发了我们的 tile-based 渲染算法
  • specular effects
    • Neural Point Catacaustics：使用 MLP 而不是 CNN，时间上稳定了，但还是需要 MVS 输出的几何
  • 相关工作挺多的，之后再细看

Overview

  • 输入为静态场景的多视角图片
  • SfM 生成相机位姿，同时生成稀疏点云
  • 通过稀疏点云初始化 3D Gaussian
    • position (mean), covariance matrix and opacity \(\alpha\)
  • 方向材质使用 SH
  • 优化、渲染
  • tile-based rasterizer

Differentiable 3DGS

  • Differentiable 3D Gaussian Splatting
  • 起点：SfM 输出的不带法向的稀疏点云
  • 我们的方法和之前工作使用的 2D 点类似
  • 稀疏点云估计法向很困难，粗糙的法向效果也并不好，于是我们使用不依赖于法向的 3D Gaussian
  • 3DGS 定义（世界坐标）
    • full 3D covariance matrix \(\Sigma\)
    • 中心位置 mean \(\mu\)

\[ G(x) =\exp\left(-\frac{1}{2}(x)^T\Sigma^{-1}(x)\right) \]

  • 如何从 3D 渲染到 2D：2001 年的 EWA Volume Splatting 算法
  • 相机空间中的 covariance matrix \(\Sigma'\) 如下，推导见副录
    • viewing transformation \(W\)
    • \(J\)​：affine approximation of the projective transformation
    • \(JW\)：世界空间转换到相机屏幕空间

\[ \Sigma'=JW \Sigma W^TJ^T \]

  • 一个优化方法：\(\Sigma\) 表示 radiance field
    • 问题：\(\Sigma\) 只有半正定，才有物理意义
    • 梯度下降的优化过程很难保证半正定
  • 使用更加直接的方式进行
    • 为什么没有平移？看副录的推导，和平移无关
    • 3D 向量保存放缩分量、四元数 \(q\) 保存旋转分量（注意需要对 \(q\) 归一化）

\[ \Sigma=RSS^TR^T \]

  • 让自动微分更快，我们显式求导：\(\dfrac{\partial{\Sigma}}{\partial{s,q}}\)
  • 各向异性的协方差表示，能够很好的适应场景中不同的形状

Optimization

  • Optimization With Adaptive Density Control of 3D Gaussians
  • 优化
    • \(p,\alpha,\Sigma\)
    • SH 的系数（视角相关的现象）
    • 3DGS 的密度

Optimization

  • 生成的几何位置可能不准，需要实现如下的功能
    • create、destroy、move geometry
  • 3DGS 的质量很关键
    • 因为可能存在这样的情况：一个高斯就表达了一整块同质（homogeneous）的区域
  • SGD 优化（Stochastic Gradient Descent）
  • fast rasterization 很重要（是优化的瓶颈）
  • 激活函数
    • \(\alpha\)：sigmoid，将其限制到 \([0,1)\)
    • \(\Sigma\) 的放缩分量：指数激活函数（类似原因是什么意思？）
1
2
3
4
5
6
7
8
9
self.scaling_activation = torch.exp
self.scaling_inverse_activation = torch.log

self.covariance_activation = build_covariance_from_scaling_rotation

self.opacity_activation = torch.sigmoid
self.inverse_opacity_activation = inverse_sigmoid

self.rotation_activation = torch.nn.functional.normalize
  • 初始化
    • \(\Sigma\) 初始化为各向同性的，轴等于到最近三个点的距离的平均值
  • loss
    • \(\lambda=0.2\)

\[ \mathcal{L}=(1-\lambda)\mathcal{L}_1+\lambda\mathcal{L}_\text{D-SSIM} \]

Adaptive Density Control

  • Adaptive Control of Gaussians
  • optimization warm-up
  • 每经过 100 次迭代，对 GS 进行加密，去除透明 GS（\(\alpha<\epsilon_{\alpha}\)）
  • 如下区域的 view-space positional 梯度都比较大（因为尚未重建好）
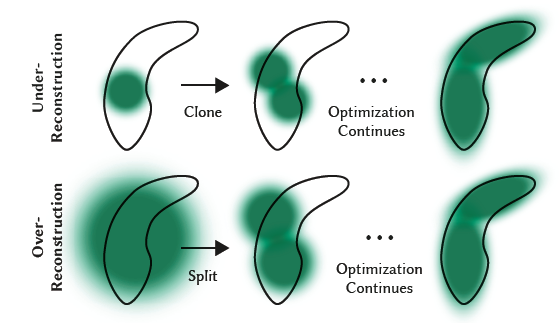
    • regions with missing geometric features （“under-reconstruction”）
    • Gaussians cover large areas in the scene（“over-reconstruction”），内部高方差
  • 加密如上区域，如果 GS 的 view-space positional 梯度大于 \(\tau_{\text{pos}}=0.0002\)，就加密
    • under-reconstruction：复制一份 GS，往梯度方向平移
      • 总体积增大、GS 数量增加
    • over-reconstruction：分裂，scale 变成原来的 \(1/\phi=1/1.6\)（实验获得），位置通过将原来的 GS 作为采样 pdf 采样得到
      • 总体积减小、GS 数量增加

  • 问题：floaters close to the input cameras 的时候，优化出问题
    • 导致 GS 数量激增
    • 解决方案，每 \(N=3000\) 次迭代之后，将 \(\alpha\) 往 0 附近设置
      • 这样如果 GS 是有用的话，会将 \(\alpha\) 优化变大；如果无用则会被剔除
  • 我们周期性的去除很大的 GS
    • very large in worldspace
    • have a big footprint in viewspace
  • GS 作为欧几里得空间中的原体，一直存在

Fast Differentiable Rasterizer

  • Fast Differentiable Rasterizer For Gaussians
  • 启发：软光栅（Pulsar，CVPR 2021）
  • 将屏幕划分为 16x16 的 tile
  • 根据视锥体（view frustum）对 GS 进行 culiing
    • 只保留和视锥体相交的置信区间为 99% 的 GS
    • guard band：直接剔除极端的 GS（靠近相机近平面的、视锥体外很远的），计算他们的 projected 2D covariance 不稳定
  • 对每个 GS，对其覆盖到的每一个 tile 实例化一个 key（view space depth and tile ID）
    • 覆盖多个，则有多个 key
    • key：一个 uint64，高位 tile ID，低位深度值
  • 对 key 排序：single fast GPU Radix sort
    • 只排一次，没有 per-pixel ordering
    • \(\alpha\)-blending 可能会有 alias，但是当 splats 和像素大小相近时，基本上看不出来
    • 大大加速了训练和渲染（在收敛的场景中没有明显可见的 artifacts）
  • Radix sort 排序结束之后，tile ID 相同的就会被聚到一起（key 的设计保证了这一点）
    • 每一个 tile 都能通过 first and last depth-sorted entry 获取到整个 GS 有序列表
    • tile 内部共享这个列表
  • 光栅化：forward pass
    • 一个 tile 一个线程块（thread block），便于使用 shared memory 共享数据读取
    • 利用 shared memory（16x16），一起读取 GS（front-to-back）
      • 一次读取 16x16，循环读取
    • 当 \(\alpha\) 累计到指定值的时候，该像素对应的线程停止计算
      • T 小于一定值（0.0001），计算的式子
      • 一些实现的细节，为了数值稳定（clamp \(\alpha<0.99\)，\(\alpha<\epsilon=1/255\) 时忽略该 GS）
    • 排序细节：副录C
  • 光栅化中，T 作为唯一停止条件，不限制 GS 的个数
  • backward pass
    • 需要对所有的相关 GS 计算 loss
    • 重新过一遍 list，这样不需要保存相关数据
      • 之前：保存相关数据，将其保存在 global memory 中，需要处理动态长度的数据
    • back-to-front：方便计算梯度
      • 如计算的式子所示，我们还需要知道 T
        • 只需要在 forward pass 的时候记录最终的 T\(=\prod_{j=1}(1-\alpha_j)\)
        • 逆向遍历的时候除去后面的就行了

结果

Implementation

  • PyTorch 框架
  • CUDA kernels for rasterization（前向渲染、反向计算 loss）
  • NVIDIA CUB：基数排序
  • open-source SIBR：interactive viewer

Optimization Details

  • warm-up：为了训练的稳定性，先在小分辨率上进行训练（4x smaller）
    • 250、500 的时候分辨率 x2
  • SH coefficient optimization
    • 对角度信息敏感
    • 如此效果才好：a central object is observed by photos taken in the entire hemisphere around it
    • 一开始只优化 0 阶的，每 1000 个迭代轮增加 1 阶，直到 4 bands of SH 都被优化

Results and Evaluation

  • 场景：13 real scenes
    • published datasets
    • synthetic Blender dataset
  • an A6000 GPU
    • Mip-NeRF360：4-GPU A100 node（等效相同时间，但是 A100 性能比 A6000 好）
  • 对比算法：Mip-NeRF360（我们实现的）、InstantNGP、Plenoxels
  • metric：PSNR, L-PIPS, and SSIM
  • 3DGS
    • 7K iterations（~5min）大部分场景，效果就不错了
    • 30K iterations（~35min），有些场景需要久一点
  • 自然数据上
    • 我们训练时间和训练快的（InstantNGP）差不多
    • 质量上和 sota 差不多（Mip-NeRF360）
    • 而且能够实时渲染
  • 合成数据集上，我们很容易 sota
    • 视角多、相机准
    • 即使随机初始化效果也很好
  • 模型大小也比较小（~3.8MB）（和基于点的方法相比）
    • 2 degree SH

Ablations

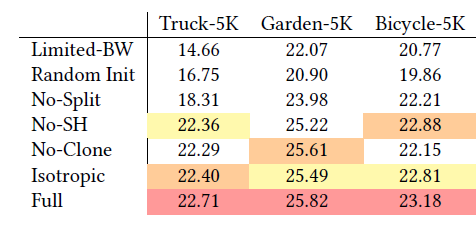
  • Initialization from SfM
    • 没有的话我们效果也还不错，但是对于（缺乏训练视角的细节）或者（背景部分），可能会丢失细节
  • Densification
    • 分裂对背景至关重要
    • 复制能加快收敛，尤其是一些细节部分（thin）
  • Unlimited depth complexity of splats with gradients
    • 只计算 top-N 重要的 GS（N=10）：效果很差
  • Anisotropic Covariance
    • 只用一个半径，结果很糊
  • Spherical Harmonics

Limitations

  • In regions where the scene is not well observed we have artifacts
    • Gaussian 能缓解
  • popping artifacts
    • Gaussian 比较大的时候会出现
    • 可能原因：trivial rejection（culling 方式不好）、简单的 visibility 排序
    • 加正则化能缓解
  • 大场景中使用 reducing the position learning rate，可能有效
    • 目前都是一套参数
  • 内存开销比 NeRF 类方法高

结论

  • In conclusion, we have presented the first real-time rendering solution for radiance fields, with rendering quality that matches the best expensive previous methods, with training times competitive with the fastest existing solutions.
  • python 部分占据了 80% 的时间（为了方便大家使用）
    • cpp 优化会更快

副录

协方差关系

  • 原始形式

\[ \mathcal{G}_{\mathrm{V}}(\mathrm{x}-\mathrm{p})=\frac{1}{2\pi\vert\mathrm{V}\vert^\frac{1}{2}}\exp\left({-\frac{1}{2}(\mathrm{x}-\mathrm{p})^{T}\mathrm{V}^{-1}(\mathrm{x}-\mathrm{p})}\right) \]

  • 应用仿射变化 \(\mathrm{u}=\mathrm{M}\mathrm{x}+\mathrm{c}\)

\[ \mathcal{G}_{\mathrm{V}}(\Phi^{-1}(\mathrm{u})-\mathrm{p})=\frac{1}{\vert\mathrm{M}^{-1}\vert}\mathcal{G}_{\mathrm{MVM}^{T}}(\mathrm{u}-\Phi(\mathrm{p})). \]

  • 对比上下两个式子，可以得到变换前后的协方差的关系

\[ \Sigma_{\text{before}}=\mathrm{V},\Sigma_{\text{after}}=\mathrm{MVM}^{T} \]

  • 用到的只是简单的矩阵计算：\(\det(AB)=\det(A)\det(B),(AB)^{-1}=B^{-1}A^{-1},(AB)^{T}=B^{T}A^{T}\)

显式求导

  • 看论文吧，大概思路就是链式法则，然后分步求导

\[ \dfrac{\part{\Sigma'}}{\part{s}}=\dfrac{\part{\Sigma'}}{\part{\Sigma}}\cdot\dfrac{\part{\Sigma}}{\part{s}} \]