(论文)[2020-HPG] ꟻLIP: A Difference Evaluator for Alternating Images

Posted on Edited on In Views:
提出了一种针对 LDR 图片的新的误差评估标准，基于人眼感知的误差评估，考虑了观察距离、显示设备等观察因素，以及图片本身的性质（point、edge 检测）

TLDR

  • 输入为 LDR 的 RGB 图片，范围 \([0,1]\)
  • color pipeline
    • RGB -> \(\text{Y}_{\text{y}}\text{c}_{\text{x}}\text{c}_{\text{z}}\) -> 空域滤波（频率低通，高斯近似，逆傅里叶变换到空域加速）-> RGB -> clamp -> \(\text{L}^{\ast}\text{a}^{\ast}\text{b}^{\ast}\) -> Hunt 调整 -> 计算 metric（firefliers 的存在，需要压缩大的 error）
  • feature pipeline
    • edge detection：2D 高斯一阶导数
    • point detection：2D 高斯二阶导数

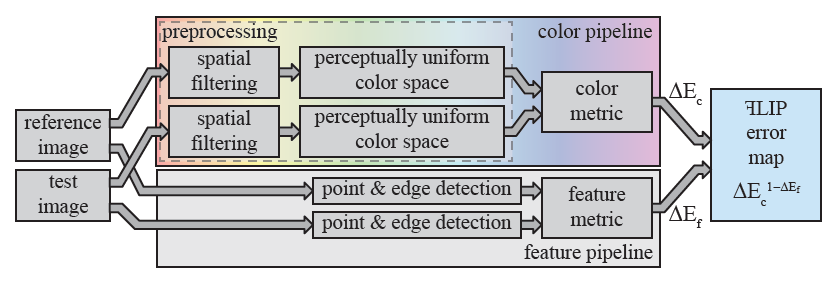
ꟻLIP

  • ꟻLIP: A Difference Evaluator for Alternating Images
    • 为了方便，下文都直接用 FLIP
  • Pontus Andersson, NVIDIA
  • 项目主页
  • 代码

Introduction

  • Flipping/Alternating 两张图片，比把两张图片并排放着，更能够看出两张图片的异同
  • 现在比较的方式：用户很难直观感受到区别
    • 并排放图片AB
    • A切换空白再切换到B
  • 渲染研究者希望是：A直接切换到B（最直观）
  • FLIP：希望解决上面这个问题，同时考虑 error map（误差图）的影响
    • 之前的方法大多是为了解释用户对刺激的反应，而不是考虑误差图
  • 对于颜色、边界的考虑借鉴了 models of the human visual system
  • 基于渲染，还考虑了 point-like structures（例如 fireflies）的影响
  • full-reference image difference algorithm
    • 输出一张图片，表示 difference
  • 收到 iCAM framework 的启发，评估包括
    • contrast sensitivity functions
    • feature detection models
    • a perceptually uniform color space
  • 试图实现和人类感知一致的 metric
    • 做了用户实验
    • 包括自然图片与生成图片

Goals and Limitations

  • FLIP 的 error 希望正比于人眼在切换图片时的感知 error
    • flipping back and forth between the images, located in the same position and without blanking in between.
  • 和观察者的距离、像素分辨率相关
    • 需要选择一个 color space 和距离成正比
      • perceptually uniform color space
  • point content（fireflies）、edge content 的变化对于感知来说比较明显
    • 需要特别重视
  • flipping 这个操作对于渲染来说很重要，大家都是这样看 error 的
  • 设计理念
    • ease-of-use
    • 复杂度低
    • 用户指定的参数要少
    • 不能处理 HDR 图片
  • 无法检测视觉掩蔽现象（visual masking）
    • 当一个视觉刺激（目标刺激）被另一个或多个同时呈现的视觉刺激（掩蔽刺激）所干扰时，目标刺激的感知能力降低的现象。简单来说，就是一些视觉元素会干扰我们对其他元素的识别。
    • 但是我们的算法无法识别（计算机不会被干扰）

Previous Work

  • 一个 Survey：Seven Challenges in Image Quality Assessment: Past, Present, and Future Research
  • 分类：根据需要 reference 的程度进行划分
    • full-reference algorithms（FLIP 是这种）
    • reduced-reference algorithms
    • no-reference algorithms
  • 分类：出结果
    • 输出一个值：Guetzli（2017）、PieAPP（2018-CVPR）、Multi-scale Structural Similarity（2003）
    • 每个像素输出一个值（FLIP 只对比这种）
      • 表示这个像素有误差可见的可能性：HDR-VDP-2（2011-SIG）、CNN-based metric（2018-TOG）
        • where the distortions are visible
      • 表示这个像素误差的大小：iCAM（2004）、S-CIELAB and CIEDE2000（2003）、SSIM（2004-TIP）、deep features（2018-CVPR）
  • 对比场景：alternating images with no blank image shown between the flips

对比算法

  • Symmetric mean absolute percentage error (SMAPE)
    • 应用：降噪网络的训练

  • SSIM
    • 与：average value, the variance, and the correlation of luminances 相关
  • S-CIELAB（FLIP 继承和发展了这个方法）
    • 考虑了 human visual system (HVS)
    • filter the images using contrast sensitivity functions
    • 在 perceptually uniform color space 中计算距离
  • HDR-VDP-2
    • 输出 error 被发现的概率，HDR（设计应用）/LDR 都可以使用
  • 网络
    • 网络的中间表示能用于计算区别
    • PieAPP：网络输出每张图的失真程度
    • user markings：输出 visibility map
  • Butteraugli：part of the Guetzli system to optimize JPEG compression

Algorithm

  • FLIP 输出 error map，每个点的值正比于感知误差的大小
  • FLIP pipeline 如下
    • color pipeline
      • spatial filter
        • 基于 human visual system’s contrast sensitivity functions (CSFs)
        • 去除在给定观察距离、给定像素分辨率下感知不到的高频信息
      • 转化成：perceptually uniform color space (PUCS) \(\text{L}^{\ast}\text{a}^{\ast}\text{b}^{\ast}\)
        • one achromatic（明度）and two chromatic components（颜色相关）
        • 简单，但是有缺陷
        • 不能处理 Hunt effect（随着亮度的增加，人们对颜色的感知也会变得更加鲜艳）
      • 为了处理 Hunt effect，我们做简单调整
      • 计算 difference，映射到 \([0,1]\)
    • feature pipeline

Color Pipeline

  • 输入为 sRGB（\(\{R_s,G_s,B_s\}\)），处理完之后要考虑 Hunt 效应（低亮度的 chromatic errors 要变小）

Spatial Filtering

Step 1

  • 先线性化成 \(\{R',G',B'\}\)
    • standard linearization formula
    • 代码里是这么写的，3 通道分别计算
1
2
3
4
5
6
7
// cpp/FLIP.h
HOST_DEVICE_FOR_CUDA static inline float sRGBToLinearRGB(float sC) {
    if (sC <= 0.04045f) {
        return sC / 12.92f;
    }
    return powf((sC + 0.055f) / 1.055f, 2.4f);
}
  • spatial filtering 在补色空间中做
    • CSFs 中：1 achromatic channel, 1 red-green channel, and 1 blue-yellow channel
    • S-CIELAB research 中使用的会带来 undesirable color shifts
    • 我们选择 \(\text{Y}_{\text{y}}\text{c}_{\text{x}}\text{c}_{\text{z}}\) 空间（\(\text{L}^{\ast}\text{a}^{\ast}\text{b}^{\ast}\) 的线性版本）
      • \(\text{Y}_{\text{y}}\)：achromatic channel
      • \(\text{c}_{\text{x}}\)：red-green channel
      • \(\text{c}_{\text{z}}\)：blue-yellow channel
  • 转换
1
pImage[i] = color3::XYZToYCxCz(color3::LinearRGBToXYZ(pImage[i]));
具体转换逻辑如下，点击展开 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
HOST_DEVICE_FOR_CUDA static inline color3 LinearRGBToXYZ(color3 RGB) {
    // Source: https://www.image-engineering.de/library/technotes/958-how-to-convert-between-srgb-and-ciexyz
    // Assumes D65 standard illuminant.
    const float a11 = 101355520f / 24577794.0f;
    const float a12 = 8788810.0f / 24577794.0f;
    const float a13 = 4435075.0f / 24577794.0f;
    const float a21 = 2613072.0f / 12288897.0f;
    const float a22 = 8788810.0f / 12288897.0f;
    const float a23 = 887015.0f / 12288897.0f;
    const float a31 = 1425312.0f / 73733382.0f;
    const float a32 = 8788810.0f / 73733382.0f;
    const float a33 = 70074185.0f / 73733382.0f;
    color3 XYZ;
    XYZ.x = a11 * RGB.x + a12 * RGB.y + a13 * RGB.z;
    XYZ.y = a21 * RGB.x + a22 * RGB.y + a23 * RGB.z;
    XYZ.z = a31 * RGB.x + a32 * RGB.y + a33 * RGB.z;
    return XYZ;
}
//
//
HOST_DEVICE_FOR_CUDA static inline color3 XYZToYCxCz(color3 XYZ, const color3 invReferenceIlluminant = INV_DEFAULT_ILLUMINANT) {
    // The default illuminant is D65.
    XYZ = XYZ * invReferenceIlluminant;
    float Y = 116.0f * XYZ.y - 16.0f;
    float Cx = 500.0f * (XYZ.x - XYZ.y);
    float Cz = 200.0f * (XYZ.y - XYZ.z);
    return color3(Y, Cx, Cz);
}
  • 现在得到了 \(\{S_{\text{Y}_{\text{y}}},S_{\text{c}_{\text{x}}},S_{\text{c}_{\text{z}}}\}\)

Step 2

  • CSFs 对于敏感度的定义：cycles per degree of visual angle 的函数
    • 我们这里进行转化，one cycle corresponds to two pixels
  • 与观察距离和像素分辨率相关，计算 PPD（pixels per degree）\(p\)
    • 观察距离 \(d\) 米
    • 显示屏大小（单位米）：\(W_{\text{m}}\times H_{\text{m}}\)
    • 分辨率：\(W_{\text{p}}\times H_{\text{p}}\)

\[ p=d\dfrac{W_{\text{p}}}{W_{\text{m}}}\dfrac{\pi}{180} \]

Step 3

  • 频域滤波：选择滤波器，频率滤波转换为空域滤波，\(3\sigma\) 确定空域的范围
  • 我们是基于 1988 年的 CSFs，但是这些 CSFs 不是度量 \(\text{Y}_{\text{y}}\text{c}_{\text{x}}\text{c}_{\text{z}}\) 空间的
    • 但是这个带来的 inaccuracy 是微不足道的
    • CSFs：频域
      • achromatic CSF：带通滤波器（bind-pass filter）
      • chromatic CSF：低通滤波器（low-pass filter）
  • 我们需要保留直流分量（DC），因此都修改为低通
    • 直流分量表示平均值（不变的）
  • low-pass filter 如下

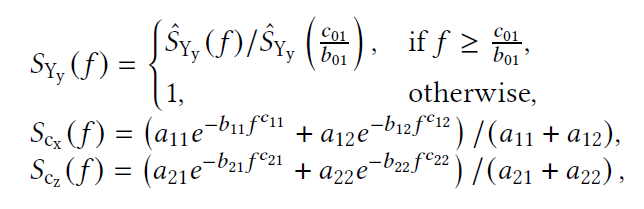
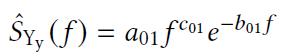
  • GPU 快速 filter，将其转化为 Gaussians 的和
    • 直接使用上面的低通会导致振铃效应（ringing artifacts）
    • 每个通道，我们使用 1-2 个 zero-centered Gaussian 代替
  • 频域高斯

\[ G(f)=ae^{-bf^2} \]

  • 转化为空域（逆傅里叶变换）：\(\sigma=\sqrt{\dfrac{b}{2{\pi}^2}}\)

\[ g(x)=a\sqrt{\dfrac{\pi}{b}}\exp(-\frac{\pi^2}{b}x^2) \]

  • 使用 Matlab 找到最优近似：近似的时候是近似频域得到最优的 \(b(,a)\)
    • filter 之后有归一化，因此如果只有一个 Gaussian 的话，倍数系数不用管
    • 两组表示两个
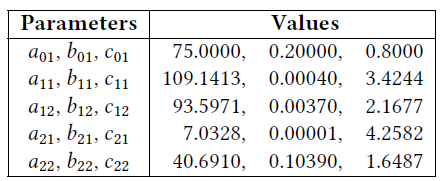
参数 值
\(b_{\text{Y}_{\text{y}}}\) 0.0047
\(b_{\text{c}_{\text{x}}}\) 0.0053
\(a_{\text{c}_{\text{x}}},b_{\text{c}_{\text{x}}}\)（2 组） (34.1,0.04), (13.5,0.025)
  • 频域区间：\(\left[-\dfrac{p}{2},\dfrac{p}{2}\right]\)，\(p\) 为采样频率
    • S-CIELAB and CIEDE2000 工作
  • 转换为空域：\(\Delta=\dfrac{1}{F_s}=\dfrac{1}{p}\)
    • \(\Delta\)：刚好对应频率中最近的两个采样点在空域中的距离
    • 单个高斯模型，\(3\sigma\) 保留了 99.7% 的能量
    • 因为我们使用的高斯都是 zero-centered，使用最大的 \(3\sigma\) 就能保证所有高斯都保留 \(\ge\) 99.7% 的能量
    • 这里直接考虑保留空域中高斯的 \(3\sigma\)（神奇，我还以为会考虑频域，转化到空域）
      • \(b_{\max}=0.04\)

\[ \begin{aligned} r_{\max} &=\left\lceil{\sqrt{\dfrac{3\sigma_{\text{space}\max}}{\Delta}}}\right\rceil\\ &=\left\lceil{\sqrt{3p\cdot\dfrac{b_{\max}}{2{\pi}^2}}}\right\rceil\\ \end{aligned} \]

  • 1D filter 的范围

\[ 0,\pm\Delta,\pm2\Delta,\cdots,\pm r\Delta \]

  • 2D filter 的范围

\[ \begin{array}{c} \text{evaluate}:d(x,y)=\Delta\sqrt{x^2+y^2}\\ (x,y),x,y\in\{0,\pm1,\pm2,\cdots,\pm r\}\\ \end{array} \]

  • 权重归一化
  • 现在得到了 filtered colord \(\left\{\widetilde{\text{Y}}_{\text{y}},\widetilde{\text{c}}_{\text{x}},\widetilde{\text{c}}_{\text{z}}\right\}\)
  • 需要转换到 RGB 空间，然后 clamp 到 \([0,1]^3\) 之间
    • 不然 filter 之后可能超出 RGB 范围

Perceptually Uniform Color Space

  • 这个空间中的距离和感知距离成正比
  • clamp 之后的 RGB 转化到 \(\text{L}^{\ast}\text{a}^{\ast}\text{b}^{\ast}\) 空间，得到 \(\left\{\widetilde{L^{\ast}},\widetilde{a^{\ast}},\widetilde{b^{\ast}}\right\}\)
1
2
// Move from linear RGB to CIELab.
filteredYCxCzReference = color3::XYZToCIELab(color3::LinearRGBToXYZ(filteredYCxCzReference));
具体转换逻辑如下，点击展开 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
HOST_DEVICE_FOR_CUDA static inline color3 XYZToCIELab(color3 XYZ, const color3 invReferenceIlluminant = INV_DEFAULT_ILLUMINANT) {
    const float delta = 6.0f / 29.0f;
    const float deltaSquare = delta * delta;
    const float deltaCube = delta * deltaSquare;
    const float factor = 1.0f / (3.0f * deltaSquare);
    const float term = 4.0f / 29.0f;
    // The default illuminant is D65.
    XYZ = XYZ * invReferenceIlluminant;
    XYZ.x = (XYZ.x > deltaCube ? powf(XYZ.x, 1.0f / 3.0f) : factor * XYZ.x + term);
    XYZ.y = (XYZ.y > deltaCube ? powf(XYZ.y, 1.0f / 3.0f) : factor * XYZ.y + term);
    XYZ.z = (XYZ.z > deltaCube ? powf(XYZ.z, 1.0f / 3.0f) : factor * XYZ.z + term);
    float L = 116.0f * XYZ.y - 16.0f;
    float a = 500.0f * (XYZ.x - XYZ.y);
    float b = 200.0f * (XYZ.y - XYZ.z);
    return color3(L, a, b);
}
  • 考虑 Hunt 效应：除了亮度都一样
亮度低，对比弱 亮度高，对比强

  • 转换为 \(\left\{\widetilde{L_{\text{h}}^{\ast}},\widetilde{a_{\text{h}}^{\ast}},\widetilde{b_{\text{h}}^{\ast}}\right\}\)

    • \(L\) 本身范围就是 [0, 100]，\(a,b\) 没有限制

    • 直观上理解：给 \(a,b\) 的差距乘上 \(L\) 作为系数

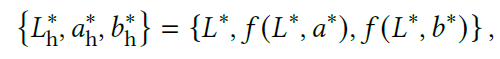
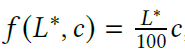
Color Metric

  • 之前的 metric 只在 distance 比较小的时候有用
  • 渲染的 distance 可能很大：fireflies
  • HyAB：a metric designed to handle larger color distances
    • HyAB distance, \(\Delta\text{E}_{\text{HyAB}}\)

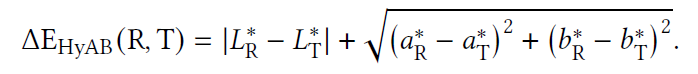
  • 最大为 \(308\)
    • 输入 RGB 为（\(\{0,0,1\},\{0,1,0\}\)）
    • 全黑白是 \(100\)
  • reduce the gap between large differences in luminance versus large differences in chrominance
    • 高端（接近 1 部分）压缩
    • 进行一个映射：\(q_c=0.7\)

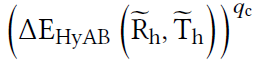
  • 映射之后
    • 此时上面最大值为：203（Hunt adjusted 之后变了，但还是最大值）
    • \(q_c\) 映射之后：41
  • 之后再归一化到 \([0,1]\)
  • 归一化的时候，进一步对 big value 进行压缩
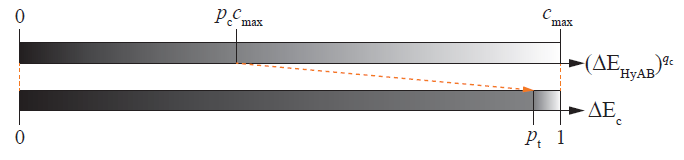
    • 给两个超参：\(p_c=0.4, p_t=0.95\)
      • 映射：输入为 \(\Delta\text{E}_{\text{HyAB}}\)
        • \([0,p_cc_{\max})\to[0,p_t)\)：线性映射
        • \([p_cc_{\max},c_{\max}]\to[p_t,1]\)：用上面的压缩

Feature Pipeline

  • 之前的工作能比较好检测 edge，但是对 point 不太行
  • 两张图都过一遍，对比响应不同的地方

Feature Detection

  • 转换到 \(\text{Y}_{\text{y}}\text{c}_{\text{x}}\text{c}_{\text{z}}\) 空间，然后在 \(\text{Y}_{\text{y}}\) 做 feature detection
    • 高频空间信息基本都在这个通道上
    • 归一化到 \([0,1]\)
  • 输出值都在 \([0,1]\) 之间
  • kernel 卷积，权重和都为 1/-1
  • ppd（\(p\)）相关（pixel per angle）
  • edge 检测：2D 对称高斯的一阶微分
    • 人眼对边缘的响应：\(\omega=0.082 \deg\)
    • 我们使用的 filter 的标准差：\(\sigma(w,p)=\dfrac{1}{2}wp\)
      • filter 半径为 \(3\sigma\)
      • \(\lceil3\sigma(\omega, p)\rceil\) pixels
    • 实现上，\(x,y\) 方向各来一遍，得到的图片记作 \(\Vert\nabla \mathrm{I}\Vert\)，每个像素对应的值称为 edge feature value
  • point 检测：2D 对称高斯的一阶微分
    • 参数和实现都类似
    • 得到的图片记作 \(\Vert\nabla \mathrm{I}^2\Vert\)，每个像素对应的值称为 point feature value

Feature Metric

  • edge/point 不太会出现在同一个像素里
  • \(q_{\text{f}}=0.5\)
    • \(/\sqrt{2}\)：让结果在 \([0,1]\) 之间，为啥？

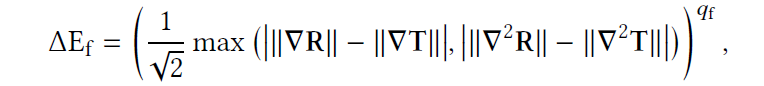
Final Difference Map

  • 都是 \([0,1]\)

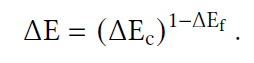
Pooling

  • 降分辨率，特殊的变成一个值
  • 信息不可逆的丢失
  • 压缩数据

histogram

  • histogram：\(x\to n(x)\)
    • weighted histogram：\(n\to x\cdot n(x)\)
  • spp 越高，error 越集中在小的部分，但是高 error 的数量也在增加（firefly 的概率在增加）
    • firefly 的问题可能导致 spp 增加时，error 有所增加
  • 进一步压缩
    • weighted median and the arithmetic mean
      • mean：容易求导，可以用于 NN
    • 25% and 75% weighted percentiles (first and third weighted quartiles)：分位数
    • the minimum value, and the maximum value

Evaluation

  • 两个部分
    • analyze the error maps
    • user study
  • 数据集
    • 自己生成
    • 前人：LocVis、the CS-IQ image data bases、\(\cdots\)
  • artifacts 类型
    • aliasing、Monte Carlo noise、color shifts
    • 退化的自然图片：compression、dither（抖动）、blur、contrast changes
  • 对比 metric：为了展示，都调整输出到 \([0,1]\)
    • HDR-VDP-2、LPIPS、the CNN visibility metric(CNN, for short)、Butteraugli
      • 输出的 \([0,1]\)，error 小到大，修改他们的 color 映射到我们这个
    • SMAPE：一般用于 HDR
    • Euclidean RGB distance
      • 可能的最大值认为是 RGB cube，归一化
    • S-CIELAB
      • 最大值为 259（blue、green）
    • SSIM：\([-1,1]\)
      • no error：1，max error：0
      • negative values can arise due to the correlation factor
      • \(s'=1-s\)
    • PieAPP：\((-\infty,\infty)\)
      • no error：0，max error：\(\pm\infty\)
      • \(a'=\left\vert{2-\dfrac{1}{1+e^a}}\right\vert\)
  • 项目主页上有展示

Analysis

Figure 9

  • 每一个方法和 FLIP 比一张图
  • CNN、LPIPS、PieAPP
    • 定位不准（网络方法的通病）（localization）
    • 会将 error 部分的周围也当作 error（扩散）
  • HDR-VDP-2
    • ringing artifacts
    • 但是说实话这里 diffuse 的那种噪声 FLIP 显示的不好
  • Butteraugli
    • 偶尔会对不明显的差异反应过度
    • localization 问题
  • S-CIELAB
    • band-pass filter 的问题，会导致全局的 blur
      • filter 之后平均了整体的灰度，导致结果上相似，error 不见了

  • SSIM
    • 没有考虑 pdd，导致将很多观察不到的误差都展示出来了
    • 有一些不可解释的结果值
  • SMAPE
    • 因为除了像素真值（relative error），导致暗处误差放大，但实际上这些观察不到
    • FLIP 通过 Hunt-adjustment 克服了这一点

Figure 10

  • MCPT 不同 spp 结果，所有方法比 error
  • 一致性：spp 增加，error 变小（特殊：firefly 增多）
  • FLIP 处理不了的问题：masking（有大的不同，但是因为其他原因我们观察不到）
    • where image differences are present, but also hard to notice due to high amounts of irregularities or contrast shifts
    • FLIP 会 overestimation，下图是一个示例

  • 性能：180 ms
    • unoptimized GPU implementation
    • \(p=67\text{ PPD}\)
    • 1920 × 1080
    • NVIDIA RTX 2080 Ti

User Study

  • ref/test flip 切换，周期为 0.5s（每秒两张图？）
    • 图片顺序随机
    • 不同 metric 的 error map 的顺序也是随机的
  • 用户
    • 打分：0-3（metric 和 error 对应的差到好）
    • 关注异常
      • false positives (indicating differences when there are none)
      • false negatives (not indicating differences when they exist)
    • 关注 magnitude and localization
    • 距离满足 \(p=67\) pdd
  • 数据组成
    • 11 组 rendered images（R）
    • 10 组 natural images（N）
      • 8 其他数据集
      • 2 我们进行 distortion
  • 用户
    • mainly computer graphics experts
    • 还包括 color scientists and computer vision researchers
  • 结果如下：FLIP 平均分数 2.1

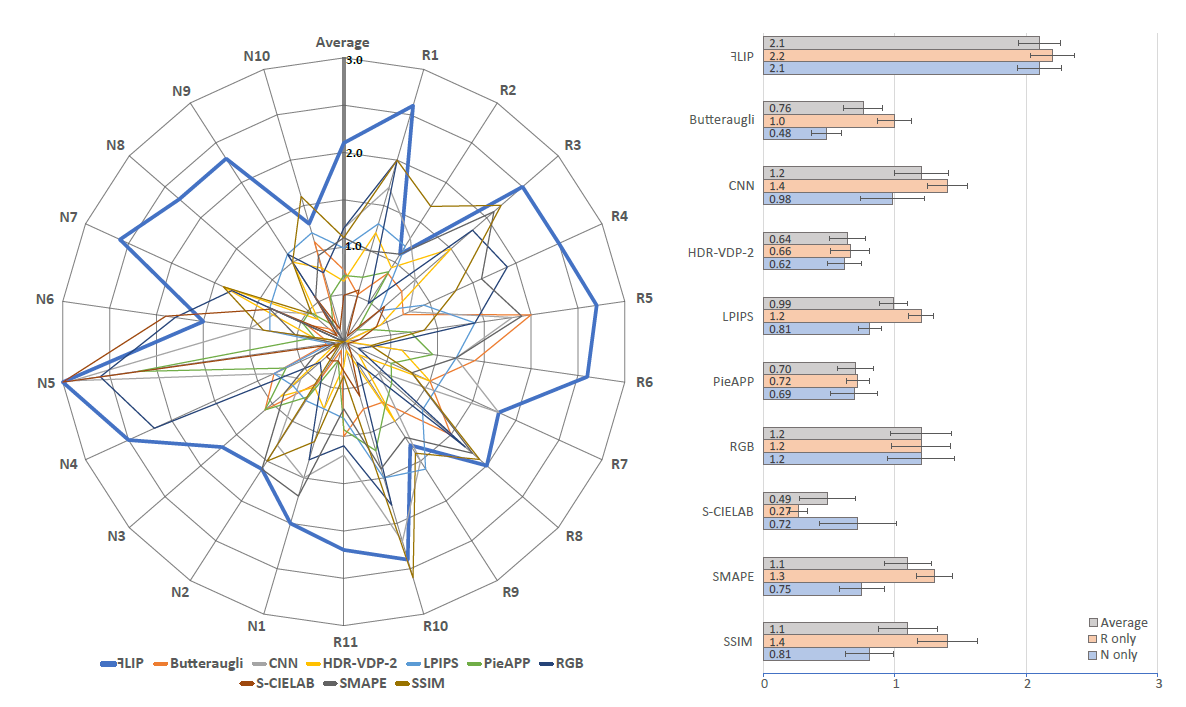
Discussion