(论文)[2022-ECCV] PRIF: Primary Ray-based Implicit Function

Posted on Edited on In Views:
学习到了一种新的神经网络隐式表示，可以用于光线与场景求交，和 SDF 不同，不需要经过 ray marching（sphere tracing），一次查询直接就能求得交点（感觉这里完全没考虑可见性问题）

TLDR

  • 任务：输入光线，输出交点位置
  • 创新点：光线的编码

PRIF

img

Introduction

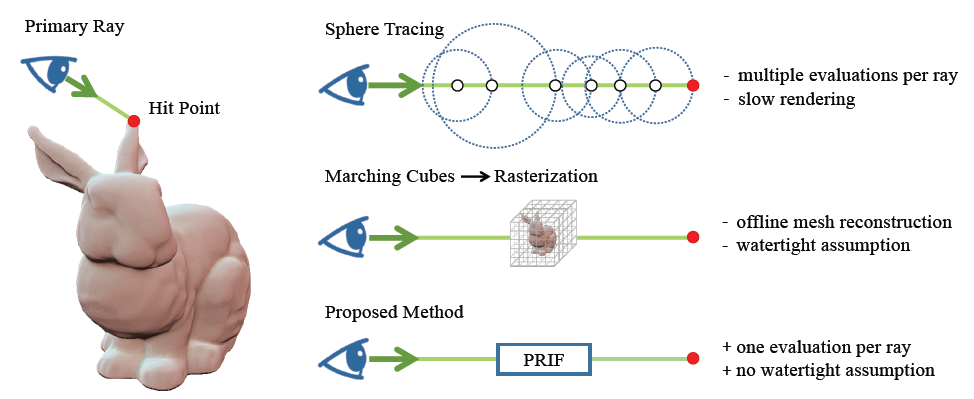
  • SDF 对于渲染来说很不友好，如下两种方法都需要多次访问 SDF
    • sphere tracing（ray marching）
    • 通过 Marching Cubes 转化为 Mesh
      • Mesh 受限于 mesh 算法（grid resolutions、shape watertightness）
  • 论文工作：将 point-based 转化为 ray-based，只需要一次查询

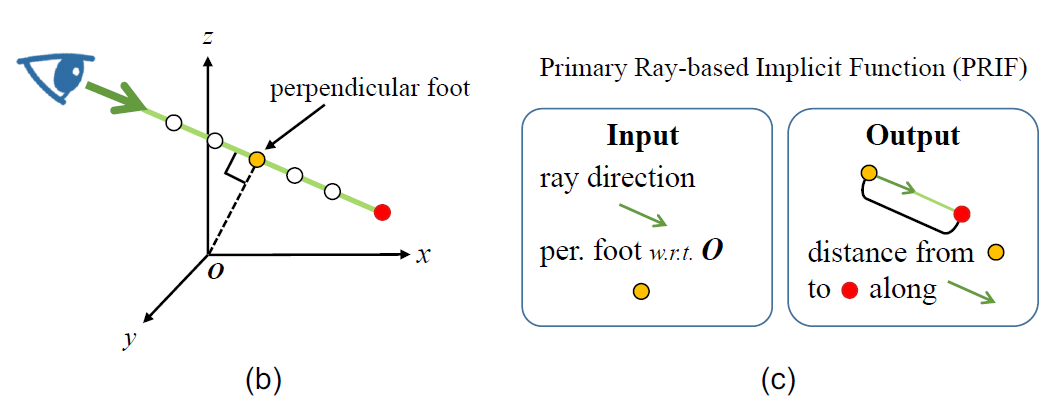
  • 光线：\(r=(\mathrm{p}_r,\mathrm{d}_r)\)
    • \(\mathrm{p}_r\in\mathbb{R}^3,\mathrm{d}_{r}\in\mathrm{S}^2\)
  • nontrivial formulation
    • \((\mathrm{p}_r,\mathrm{d}_r)\to(\mathrm{p}_{hit},\mathrm{distance}_{hit})\) 效果不好
    • 沿着方向 \(\mathrm{d}_r\) 移动原点 \(\mathrm{d}_r\)，交点不变，只有距离变化
  • 我们使用坐标原点到光线的垂足 \(\mathrm{f}_r\) 代替原点作为输出，这样原点移动，输入也不变化
    • 可见性问题如何解决？
  • 贡献
    • 提出了 PRIF（最主要的贡献）
    • PRIF 效果不错
    • PRIF 有很多应用

3D Shape Representations

Functional Representations

  • 传统 3D shape 的表示
    • polygon meshes, point clouds, and voxels.
  • 神经网络：implicit neural representations (INRs)
    • MLP 编码位置信息
    • 输出
      • OF：输出这个位置是否有东西
        • occupancy function (OF)
        • binary classification problem：1（有）0（无）0.5（是边界）
      • SDF：输出到场景中最近 shape 的距离
        • 表面：0
    • 等值面（isosurface）：continuous 3D function 的一个水平集（level set）
      • 如何提取出等值面：Marching Cubes 等 mesh 算法

Global vs Local Representations

  • 如何从 INR 中提取数据
    • 目的：rendering efficiency & representation quality
    • 一个大的方向：spatial partitions
  • Local Representations
    • divides the surfaces of shapes into different local patches
    • divides the 3D volume into small local regions
  • 本文：Global
    • a shape is represented by a single network without any spatial partitions.
    • 之前的 Local 方法会对本文效果有提升

Ray-based Neural Networks

  • 光场（light field scene）
    • map camera rays to their observed colors：\((x,y,u,v)\to(r,g,b)\)，可以实现高效+高保真的效果
    • Plucker coordinates 进行编码，实现任意起点、任意方向的光线
      • 齐次坐标编码直线：\(d,m(=x\times y)\)

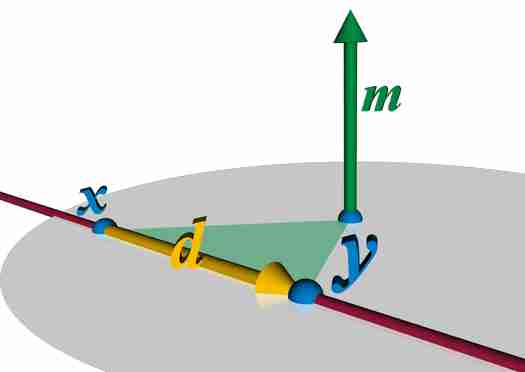
  • 我们使用垂足表示，好处是这样表示后，输出变成了输入的仿射变换

Method

Background

  • naive：\(r=(\mathrm{p}_r,\mathrm{d}_r)\to c_r=(r,g,b)\)
    • 效果不好，沿着 \(\mathrm{d}_r\) 前进一点得到的新光线 \(r'\) 的 \(c_{r'}=c_r\) ，但是网络很难保证这一点
  • Plucker coordinates
    • \(r=(\mathrm{m}_r,\mathrm{d}_r)\to c_r=(r,g,b)\)
      • \(\mathrm{m}_r=\mathrm{p}_r\times \mathrm{d}_r\)：moment vector
      • 不管 \(\mathrm{p}_r\) 在光线上怎么动，结果都相同
        • 方向相同
        • \(\mathrm{d}_r\) 不变（底不变），高不变，因此面积不变，大小不变
    • \(\mathrm{p}_r'=\mathrm{p}_r-\lambda\mathrm{d}_r\)

\[ \begin{aligned} \mathrm{p}_r'\times\mathrm{d}_r &=(\mathrm{p}_r-\lambda\mathrm{d}_r)\times \mathrm{d}_r\\ &=\mathrm{p}_r\times \mathrm{d}_r-\lambda\mathrm{d}_r\times \mathrm{d}_r\\ &=\mathrm{p}_r\times \mathrm{d}_r-\lambda\mathrm{0}\\ &=\mathrm{p}_r\times \mathrm{d}_r\\ \end{aligned} \]

Perpendicular Foot

  • 垂足：\(\mathrm{f}_{r}=\mathrm{d}_r\times(\mathrm{p}_r\times \mathrm{d}_r)\)
    • 可以验证：\(\mathrm{f}_r\cdot \mathrm{d}_r=0\)
  • 可以验证不变性

\[ \begin{aligned} \mathrm{f}_{r}' &=\mathrm{d}_r\times(\mathrm{p}_r'\times \mathrm{d}_r)\\ &=\mathrm{d}_r\times(\mathrm{p}_r\times \mathrm{d}_r)\\ &=\mathrm{f}_{r} \end{aligned} \]

  • 此时对于交点 \(\mathrm{h}_r\)，可以表示为 \(\mathrm{h}_r=s_r\cdot\mathrm{d}_r+\mathrm{f}_r\)
    • \(s_r\in \mathbb{R}\)
  • PRIF：\(r=(\mathrm{f}_r,\mathrm{d}_r)\to s_r\)
  • 也就是我们训练一个 MLP

\[ \Phi(\mathrm{f}_r,\mathrm{d}_r)= s_r \]

  • 优点：一次查询、仿射变化（输出 \(s_r\) 之后，一个仿射变化就能得到结果）

Background Mask

  • 可能存在光线不打到物体（直接打空了）
  • 我们让网络同时输出 \(a_r\in[0,1]\)，表示击中物体的概率
    • cross-entropy 计算 loss \(\mathcal{L}_a\)
  • \(a_r\) 的真实值
    • background rays：0
    • foreground rays：1
  • 总的 loss
    • \(\mathcal{F}\)：foreground rays

\[ \begin{aligned} \mathcal{L} &=\mathcal{L}_a+\mathcal{L}_s\\ &=\mathcal{L}_a+\left(\sum_{r\in\mathcal{F}}\Vert{s_r-s_r^{\text{gt}}}\Vert\right)\\ \end{aligned} \]

Outlier Points Removal

  • 相邻光线之间的 sharp surface discontinuities 会导致网络输出问题（不连续性）
  • 因此求导，丢弃导数比较大的部分
    • 实验：\(\delta=5\)

\[ \left\Vert\dfrac{\partial{s_r}}{\partial{\mathrm{p}_r}}\right\Vert\ge\delta \]

Experiments

Single Shape Representation

  • 任务1：表示单个 shape，过拟合一个 mesh，看能不能表示的比较好
  • 公平起见，使用相同的网络架构
    • DeepSDF 的网络架构：8 layers with 512 hidden dimensions and ReLU activation
  • 采样策略
    • OF、SDF：采样500'000 个点，在表面附近采样更多的点
    • PRIF：采样 50 个虚拟相机，每个相机采样 200x200 条光线
  • 学习策略
    • 100 epochs
    • lr：cosine annealing strategy：\(10^{-4}\to10^{−7}\)
  • 提取表面
    • OF、SDF：Marching Cubes，分辨率 \(256^3\)
    • PRIF：可以直接获取到稠密的点的结果
  • 评估质量：评估 8192 个点之间的 mean and median Chamfer Distance (CD)
    • OF、SDF：在 mesh 上采样 8192 个点
    • PRIF：point-based meshing algorithm Screened Poisson in MeshLab，然后采样 8192 个点

Shape Generation

  • 任务2：数据集中训练测试，测试没见过的物体的效果
    • 这里的泛化性来自于 DeepSDF 的网络架构

Shape Denoising and Completion

  • 在一组物体上训练好之后，然后在没见过的物体上执行降噪或者补全

Analysis and Ablations

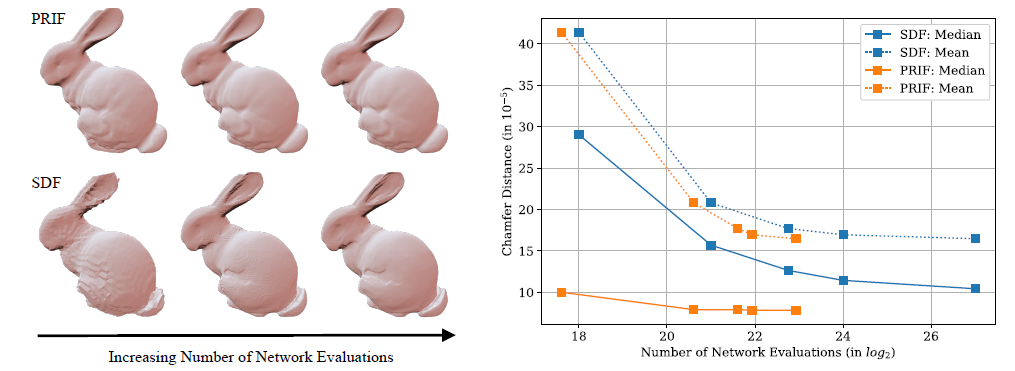
Complexity Analysis

  • 相当于评估网络本身能学习到的东西有多少
  • SDF、OF：调整 Marching Cube 的分辨率，对比结果
  • PRIF：调整 Screened Poisson 算法中使用的相机个数与分辨率

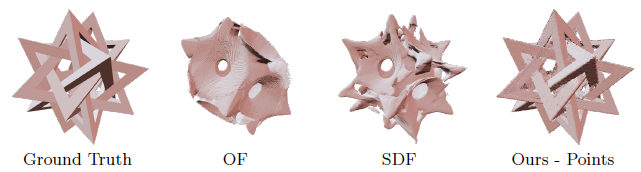
Stress Testing

  • 复杂模型：self-intersecting and non-watertight shape

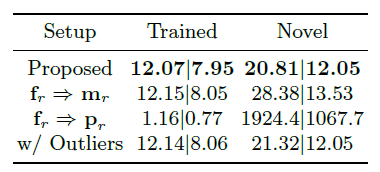
Ablations

  • w/o outlier removal
    • 指标差不多，但是会存在游离的噪点（散点）
  • \(r=(\mathrm{f}_r,\mathrm{d}_r)\)、\(r=(\mathrm{p}_r,\mathrm{d}_r)\)、\(r=(\mathrm{m}_r,\mathrm{d}_r)\)

Further Applications

  • Learning Camera Poses：固定网络，逆向学习相机参数
  • Neural Rendering with Color：讯号 PIRF 网络之后，再训练一个 \(\text{pos}\to\text{color}\) 的网络输出颜色

局限性

  • 多视角问题：需要 multi-view consistency loss or denser training views
  • 我不太理解，难道可见性问题不重要吗，好神奇，还是说单物体体现不出来，训练时间也没说
    • 感觉只是学到了最外层的点？