(论文)[2024-SIG-C] N-BVH: Neural ray queries with bounding volume hierarchies

Posted on Edited on In Views:
提出了 N-BVH，在 BVH 架构的基础上，在光线与场景求交的时候，一些子树内部节点的查询使用神经网络查询替代，从而实现场景属性的压缩，目前场景中能够学习的属性是交点、albedo、normal（其他的参数还是写死的）。速度上比 PT 慢一些，但是压缩效果很好。

TLDR

  • 任务：光追背景，输入光线，输出交点、albedo、normal
    • 生成反射光线：交点+normal（+场景中写死的BSDF参数）
  • 创新点：压缩场景（速度差不多、结果可接受的情况下，显存变为10%）

N-BVH

  • N-BVH: Neural ray queries with bounding volume hierarchies
  • Philippe Weier，DFKI，Saarland University
  • 论文：作者网站
  • 代码：Github

摘要

  • 神经网络在压缩信号方面很有效
    • 渲染中，大量存储被用于纹理和几何
    • 压缩！
  • 挑战：训练时间短、推理时间快的 trade off
  • multi-resolution hash grid
    • 使用 adaptive BVH-driven probing scheme 优化参数
  • 可以将 non-neural 和 neural 的方法结合，取各自的长处
  • 论文：Neural BVH or N-BVH（\(\mathcal{N}\text{-BVH}\)）
  • 可以实现
    • accurate ray queries
    • faithful approximations of visibility, depth, and appearance attributes

Introduction

  • BVH：加速光线与场景求交
    • 问题：内存（显存）占用过大
  • Our key observation is that any neural compression model can be optimized efficiently as long as it is trained on samples that live close to the signal of interest.
    • 神经网络总是能过拟合
  • 训练：使用场景的 BVH 生成 ray queries/responses 数据对
    • 几分钟
  • 推理：和 BVH 类似，但是不需要 full, deep BVH traversal and hence storage
  • N-BVH 可以和 standard BVH 一起使用
  • N-BVH 还有一套 simple level-of-detail (LoD) scheme
  • hash grid 的好处：稀疏编码
    • faster and easier training

贡献

  • N-BVH 的数据结构
  • neural ray-intersection query mechanism
  • fast training scheme driven by a coarse-to-fine tree-cut optimization
    • 哪里误差大优化哪里
  • multiple adaptive neural levels of-detail

应用场景

  • hybrid path tracing
  • neural appearance prefiltering
  • Neural implicit representations（神经隐式表示）
  • Geometric simplification（几何简化）
    • Silhouette and shape-preserving decimation（often with artist supervision）
    • ...
  • Neural compressed geometric reconstruction（神经压缩的几何重建）
    • 使用 SDF 替代 Mesh 表示
      • 提出（慢、低频）
      • octree feature volume：高频
      • optimized space partitioning：高压缩率、准确
    • 直接再三角形上做
    • learning visibility and depth for arbitrary ray queries
      • ray-foot parameterization 避免相同交点的混淆（\((p,d),(p+\delta d,d)\) 结果应该相同，但是简单的编码，网络很难输出相同结果）
      • 没有对几何做压缩，因此需要很大的 MLP 进行推理
      • visibility：这里的可见性指的是，只学到了最外层的点吧
    • Neural VDB
  • Hybrid neural path tracing

Method Overview

  • 使用神经网络替代 BVH Mesh
    • infer intersection point, surface normal, and appearance.
  • 基于 multi resolution hash grid
  • Neural ray inference
    • 存在误差
    • 网络大小、输入编码都会影响网络性能
      • 让样本都在表面附近 \(\to\) 高效
      • 密集采样太慢了，传统 BVH 做指导（在相交的 BVH 中进行采样）
  • a single global neural model 编码整个场景几何
  • 最终：no geometrical primitives, no textures, and only a shallow BVH
    • 压缩率高

Neural Ray Query

  • 训练：几何元素+包围盒 \(\to\) 交点信息

Motivation

  • query 最简单的参数化：ray-box entry and exit points
    • 效果差
      • 这种编码和要学习的信号（交点）相关性差
      • 导致 blur、loss in accuracy
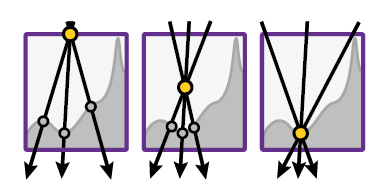
    • 下图以 entry point 为例
      • 相同的入射点，交点相差很大（网络学习到平均信息）
      • 如果 encoding point 更加接近表面，那么差距越小
      • 最理想的话直接就是交点

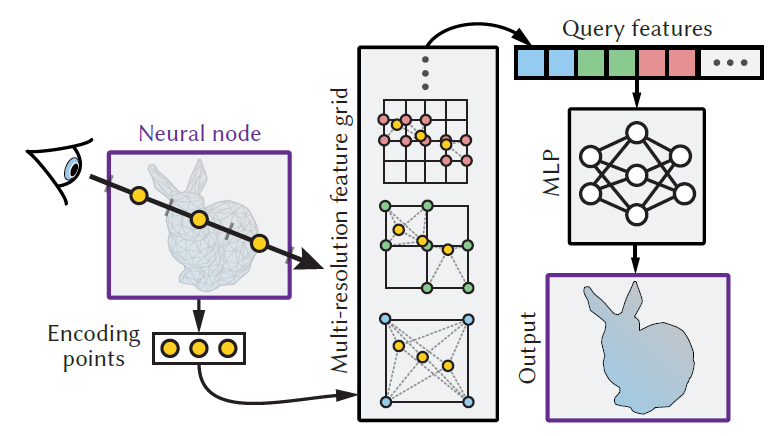
Network

  • Encoding, inference & training
  • 我们不知道交点（正是我们想计算的）
  • 输入
    • 采样若干个点形成 ray-box intersection interval
    • 保存到 multi-resolution grid 里面（经过 grid 之后，position 变成 feature）
    • concatenate（有序的，编码了方向）
    • 过小 MLP

  • pipeline
    • 采样光线
      • 均匀的场景中采样起点，50%-inflated scene bounding box（50% 膨胀的场景 AABB 包围盒）
      • 均匀采样一个方向
    • 输入模型
      • 真实值（GT）为光线与场景求交的实际结果
  • loss：根据具体信号具体设计
  • 优化：梯度下降

Sampling

  • Sampling & reconstruction quality.
  • 光线的编码：光线上的若干个点
  • 采样点
    • 例如：光线上采样 2 个点，则采样点位置为 25%，75%
      • \(x\to\dfrac{2i+1}{2x}\)，\(i=0,\cdots,x-1\)
  • 当有一个样本点在物体表面（第一个交点）的时候，效果好
    • 例子：45度倾斜的棋盘格

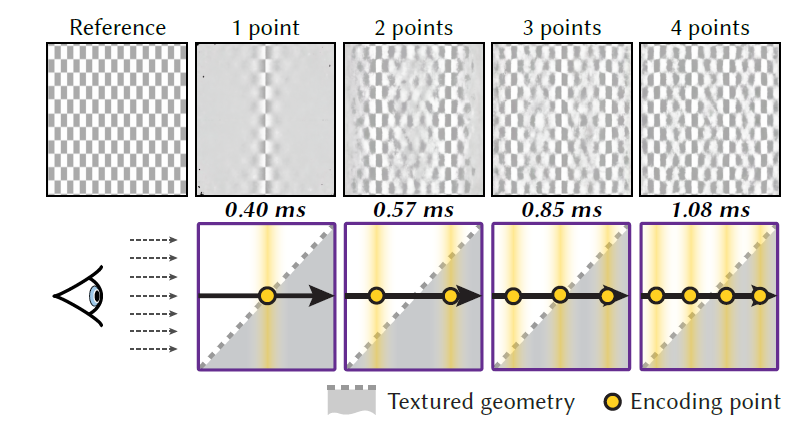
  • 期望靠近表面
    • naive：增加采样个数，开销增大
    • N-BVH 解决了这个问题（使用 BVH 做引导）

Neural BVH

  • 期望光线上的采样点靠近物体表面
  • 使用场景 BVH 作为引导，只需要考虑相交的 ray segment
    • We split the input geometry into smaller, simpler pieces, enclosing each in a tight bounding box.（似乎作者的 BVH/三角网格 特别精细？）
    • 实现了我们的目标
      • front-to back ray traversal
      • empty-space skipping
      • probing the model closer to the geometry
  • 一条光线总的查询次数（neural queries）：在找到交点之前碰到的 BVH 叶子节点个数
  • 一个浅层的 N-BVH 比使用单个 neural node 效果好很多，如下图
    • 第一排：每一个节点的平均 training loss 可视化

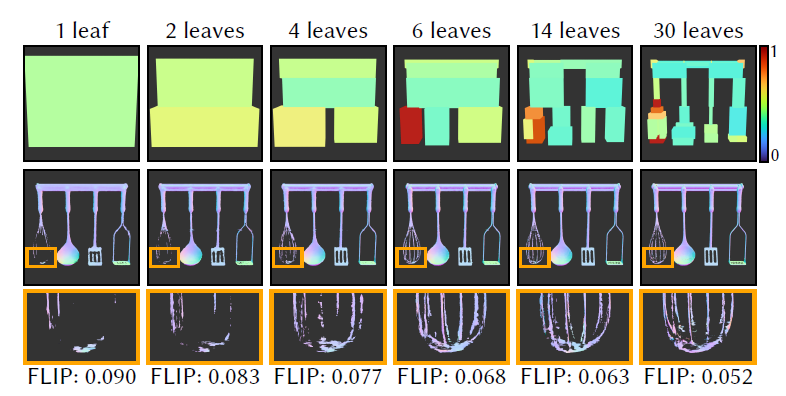
  • N-BVH 的结构
    • 和传统的 BVH 相比，节点数量更少（少1-2个数量级）
    • Nerual Node 是空心（hollow）的，具体内容是保存在1个大的网络中

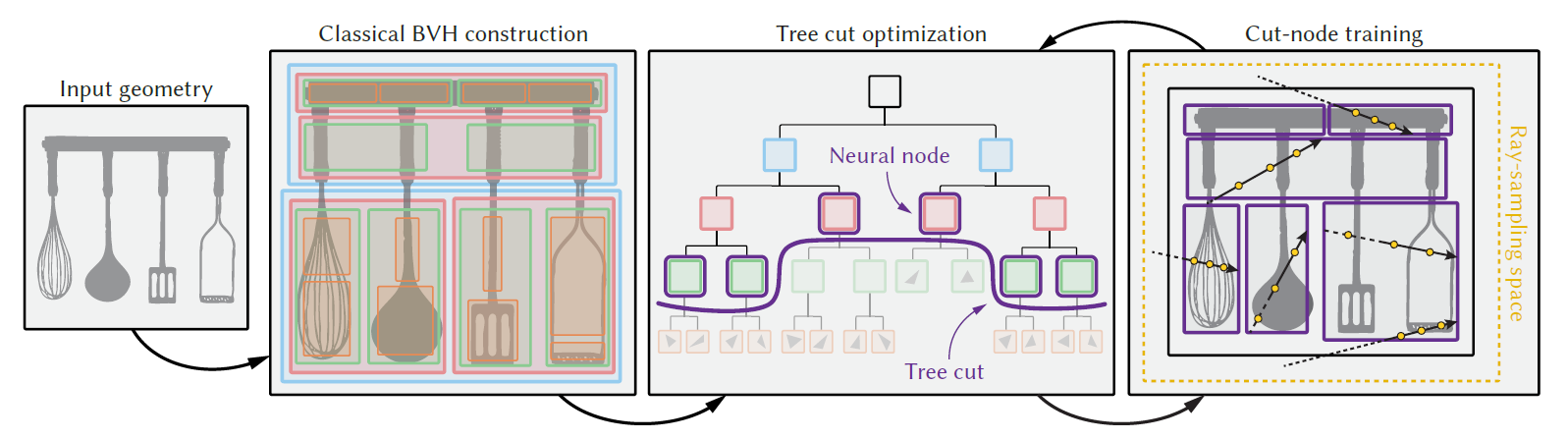
Error-driven construction

  • 想要让场景的 inference error 差不多（叶子结点的 error 相同），见上面的可视化
  • top-down approach
    • switch between model training & node splitting

Base-BVH cut optimization

  • 直接使用场景 input-geometry 的 BVH（base BVH）
  • 迭代法找到 Tree-cut（含义见图）
  • 每轮迭代：将 cut 移动的更深，cut 相邻的浅层节点作为 Neural Node
    • 先训练网络
    • 找到最大 error 的结点，使用他们的子节点替代（将子节点作为 Neural Node）
      • 分裂几个节点（top-k），由用户指定
  • 迭代次数
    • 用户指定 Neural Node 的个数，当达到用户指定值的时候，停止迭代
    • 随着迭代次数增加，cut 变大，Neural Node 增多
  • 详细算法
    • frequency \(f\)：迭代多少次分裂 nodes（更新 tree cut）
    • scaling factor \(s_n>1\)：每次分裂数目不一样，越来越多
    • scaling factor \(s_t>1\)：间隔时间越来越长（tree-cut 变大了，需要更多样本训练）
  • 参数：\(t=3000,s_t=2\)
Target node count \(f\) \(s_n\)
7 3000 2.0
155 300 2.0
1.2k 100 2.0
11k 50 2.3
33k 40 2.5
73k 50 3.2
142k 90 5.0

Node error

  • Neural Node 的 error 如何评估？

  • \(q\cdot p\)：具体的见下一个 section

    • \(q\)：node 的 training loss
    • \(p\)：random ray hit it 的概率
      • 正比于 node 的表面积（因为训练的时候光线是均匀分布在场景中的）
      • 实际实现的时候，我们使用击中当前 node 的光线比例进行估计

  • 使用 \(r\) 替代

    • \(r=2\log q+\log p=\log(q^2p)\)
    • 直接使用 top-k 的 \(p\cdot q\) 会导致对于 large and/or high-loss nodes 的过度激进分裂
    • \(\log\)：减小激进程度（log-scale）
    • \(2\)​：减小对于 large, low-loss nodes 的分裂次数（减轻 node 大小的影响）

  • 上图使用的就是 \(r\)

  • 补充材料中给出了一个复杂 mesh，对比 \(r\text{-optimization}\)​ 和 fixed-depth, uniform node splitting 相比的结果

    • \(r\) 好
    • 为什么不对比 \(r\) 和 \(p\cdot q\)

Node training and losses

  • 只训练 Neural Node 中的部分
  • 这个部分：训练 high-error 的 Node、loss

Ray distribution

  • 让 loss 分布更均匀 & 使训练更有效（limited budget）
  • 策略 1
    • 每条光线只关注第一个相交的 node
    • focuses the effort on more visible nodes
  • 策略 2：loss 小训练概率小
    • 相交的 node 以 \(\max(r/r_{\max},0.005)\) 的概率训练
    • \(r_{\max}\)：largest error in the cut（Neural Nodes）

Loss

  • Visibility
    • 在相交 ray segment（entry-exit）上的可见性问题可以被定义为一个二分问题
    • sigmoid activation
    • binary cross-entropy loss（比 L2 好）
    • 最容易学习的，用于指导其他的 loss 部分
      • 如果 gt-visibility 为 1（没有交点），那么其他的 loss 都设置为 0
      • 不需要学习（用不到）
  • Intersection point
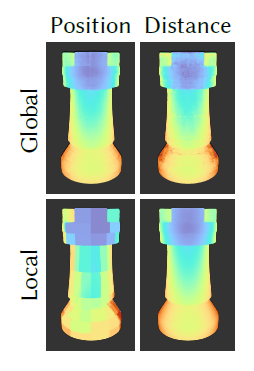
    • 备选：下图是结果的可视化，应该和上面的这个图一样
      • 1D（到光线起点的 distance），3D（位置）
      • locally（相对于 node 本身）、globally
    • 尝试后，发现 locally+1D 效果好
      • L1 Loss
    • 解释：1D 的信号更好学习

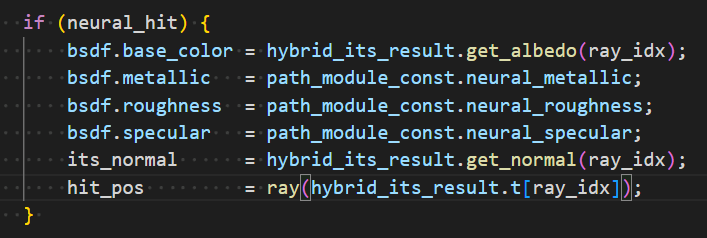
  • Auxiliary intersection data
    • 只有 normal+albedo
      • the other BSDF parameters are fixed by the user
        • 也就是说其他 BSDF 参数不能从网络中获取
    • 实验发现
      • albedo：relative L2 loss
      • normal：L1 loss

  • 2：实验发现重视 visibility 和 distance 更好

\[ L = 2L_{\text{visibility}}+2L_{\text{distance}}+L_{\text{normal}}+L_{\text{albedo}} \]

Level of detail

  • 设置 multiple base-BVH cuts，每一个对应 LoD 的一个层级
  • register a new LoD at regular training iteration intervals.
  • 随机选择一个 tree-cut（对应一个 LoD）进行训练

实现

基础

  • fully software-based CUDA wavefront path tracer
  • tiny-cuda-nn
    • half-precision scalars
  • neural prefiltering 在 RTX 3080，其他都是 RTX 3090

细节

  • BVH construction
    • N-BVH 需要自己操纵，因此不能利用硬件加速
    • CPU 建立，传到 GPU
  • 网络
    • batches size：\(2^{18}\)
    • Adam optimizer
      • lr：0.01
    • MLP
      • 4 hidden layers，64 neurons each
      • ReLU
    • 网络输出
      • normal：linear activation
      • 其他：sigmoid activation
    • hash grid
      • 8 levels：\(8^3\to1024^3\)
      • 4 features per level
    • 只通过修改 hash-map size 来调整网络大小
  • BVH 边界很小的时候，可能受到浮点数误差的影响

应用

Hybrid Path Tracing

  • 主要是起到压缩场景、减小显存开销的作用
  • TLAS + BLAS
    • each BLAS is either a classical BVH or our N-BVH
    • 一般来说，一个 mesh 一个 BLAS

结果

  • 一个示例：1920×1080
    • 只压缩复杂的东西（棋子），棋盘格没有压缩

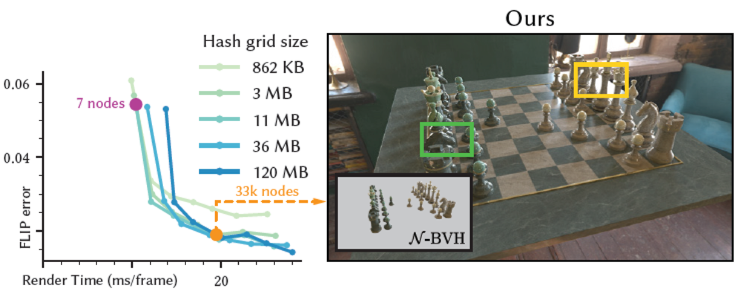
  • Reconstruction quality & performance
    • trade off
      • render times & reconstruction quality
    • 主要和 Neural Nodes 的数量相关，和 Hash Grid Size 相关性小一些
  • Compression rate
    • 通过调整 Hash Grid Size 来调整压缩率
    • Neural Node 数：33k
    • 因为有些东西不压缩，这里给了两个指标
    • 最主要的压缩来源是 mesh 的简化
    • 还放了一个 3D 扫描的 2.69G 的猛犸象

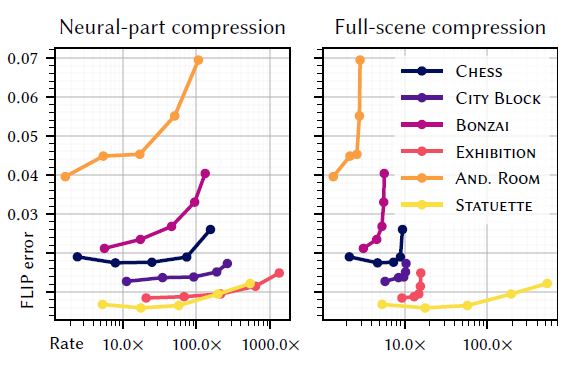
消融实验

  • Hash-grid size vs. node count
    • error 的主要影响因素：Neural Node 的数量
    • memory footprint 的主要影响因素：hash grid size（可学习参数多）
  • Training time
    • 最影响训练时间（error）的也是 Neural Node 的数量
      • 多了，traversal 的时间长了
  • Hash-grid utilization
    • mesh 分布稀疏的时候，hash grid 的优势体现出来了

Neural Prefiltering

讨论

Limitations

  • assumption of convexity (or concavity) of the geometry inside a neural node
    • 当 Neural Node 比较少的时候，存在误差
  • 局限：the fixed number of encoded points per node
    • 适应性的分布 points 个数效果会更好

Future Work

  • 泛化
    • mesh 表示到任意可以求交点的表示
    • dynamic geometry