(论文)[2020-SIG] Neural Control Variates

NCV

• Neural Control Variates
• 2020 SIGGRAPH

introduction

• MC 的加速
  • 更好的采样
    • antithetic sampling（对立采样）
    • stratification
    • quasi-random sampling
    • importance sampling
  • control variates（CV）
• 原理：根据下面式子进行转化，从而简化计算
  • \(g\)：variate control
  • \(G=\int_{\mathcal{D}}g(x)\;\mathrm{d}x\)：容易数值积分得到结果
  • 之后省略定义域 \(\mathcal{D}\)

\[ F=\int_{\mathcal{D}}f(x)\;\mathrm{d}x=\alpha\cdot G+\int_{\mathcal{D}}\left(f(x)-\alpha\cdot g(x)\right)\;\mathrm{d}x \]

• CV 的好处：让积分函数更 smooth，更容易积分
  • 典型场景：\(f/g\) 是正（负）相关的

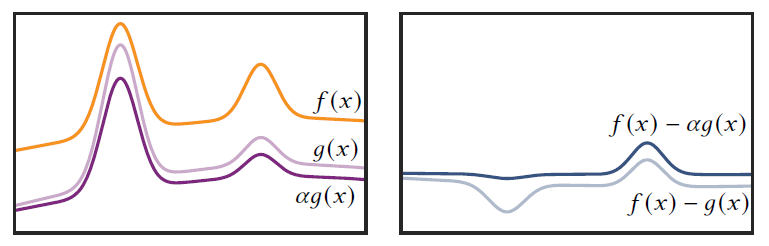
• 分解：\(g(x)=\bar{g}(x)\cdot G\)
  • shape：\(\bar{g}(x)\)
  • scale：\(G\)
• 残差部分形状可能并不好，不容易手动设计采样函数，引入 NIS
• 各自通过一个神经网络去预测 \(\bar{g}(x)\) 和 \(G\)
  • \(\bar{g}(x)\)：tailored variant of normalizing flows
  • \(G\)：a set of neural networks
• 两个损失函数
  • theoretically optimal
  • robust in practice
• NCV 的好处
  • PT 相比使用样本数更少，路径节点更短（待估计的残差部分能量更小，smooth）
    • 提前终止路径带来 bias：NCV 启发式的让 bias 最小化
  • 支持 spectral，每一个 spectral bind 使用不同的 \(g\)
    • 降低计算开销：NCV 提出一种 normalization flow，可以表示多个（最好有相关性）通道的 CV
    • 降低了 spectral noise

相关工作

• CV 的相关应用：financial mathematics and operations research（金融数学与运筹学）
• 最小方差的 \(\alpha\)
  • 使用估计积分的样本估计 \(\alpha\) 会引入偏差（Why？）
    • We resolve this issue by providing recipes for obtaining \(\alpha\) that do not bias the estimator.

\[ \alpha=\dfrac{\text{Cov}(f,g)}{\text{Var}(g)} \]

• CV 在 graphics 的应用
  • 利用 ambient illumination 加速 PT 收敛（1994，1995）
  • volumetric path tracing，near-isotropic volumes（2008）
  • 子问题：估计直接光照（2004）
• CV 的难点：如何快速估计残差积分（可能比原始积分更难重要性采样）
  • 使用 parametric trainable control variates（NIS）
• Multi-level Monte Carlo integration
  • 将 CV 引入层级结构，精细的层级给出更准确的估计
  • 问题的关键还是在如何分配样本（采样）
• NN in graphics：State of the Art on Neural Rendering
  • screen space（Deep Shading）
  • surfaces（材质模型）
  • point clouds（点云到图片）
  • free space
• Normalizing flows
  • mapping arbitrary distributions to a base distribution
  • 综述
    • 2019，Normalizing Flows for Probabilistic Modeling and Inference
    • 2019，Normalizing Flows: An Introduction and Review of Current Methods
• Control Variates based on Stein’s identity
  • 使用 score function 表示 CV：\(s(x)=\nabla\log p(x)\)，\(p(x)\) 为采样的 pdf
    • \(p(x)\) 带有参数 \(\theta\)，\(\nabla\) 对 \(\theta\) 计算
    • score function 的好处，期望为 0：\(\mathbb{E}_p[s(x)]=0\)
    • 问题
      • \(G\) 的计算困难
      • 循环依赖，更新 \(p\) 会影响残差，算残差会让 \(p\) 改变

Parametric Trainable CV