(论文)[1995-EG]Importance-driven Monte Carlo Light Tracing

Posted on Edited on In Views:
Light Tracing

MCLT

  • Importance driven Monte Carlo Light Tracing
  • EG-1995

Abstract

  • particle model

Introduction

  • 方法
    • Monte Carlo Path Tracing
      • distributed ray tracing 的一个应用
    • two pass
      • a radiosity and a ray tracing pass
    • particle tracing
      • heat transfer literature 相关
  • 算法
    • 发射 light particles
    • 采样反射方向
      • 光源：初始化为均匀分布，之后修正
      • 物体表面：BRDF

Mathematical Description

The Potential Equation

Rendering Equation

  • 光通量 flux
    • \(S\)：光源周围直接可见的物体（\(x\)）、对应的方向（\(\Theta\)）

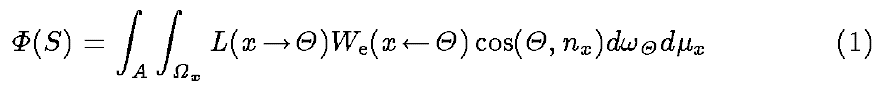
  • radiance 对面积、立体角积分得到 flux（power）
  • \(W_e\)：重要性函数

\[ W_e=\left\{ \begin{array}{cl} 1,&\text{if } (x,\Theta)\in S\\ 0,&\text{else}\\ \end{array} \right. \]

  • 需要对我们感兴趣的集合 \(S\) 进行上面积分的求解
    • classic radiosity：每一个 patch with the entire hemisphere 构成一个集合
    • ray tracing：每一个像素可见的 points and directions 构成一个集合（pixel set）
  • ray tracing 而言，我们需要对 pixel set 进行 flux 求解
    • \(W_e\) 还是定义为 pixel set 的可见位置与方向
    • 对 \(L\) 递归求解

Potential/Importance Equation

  • potential/importance equation
    • adjoint of the rendering equation（渲染方程的伴随问题）
  • pixel set 的 flux 的表达形式
    • \(S=(x,\Theta)\) ：所有光源的发射位置、方向
    • \(W\)：\(L_{\text{e}}\) 在这个方向上贡献给当前像素的百分比

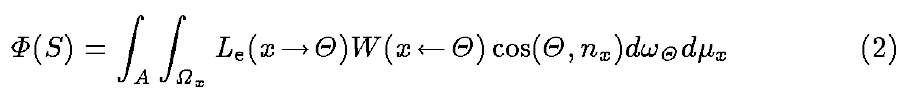
  • \(W\) 的传输

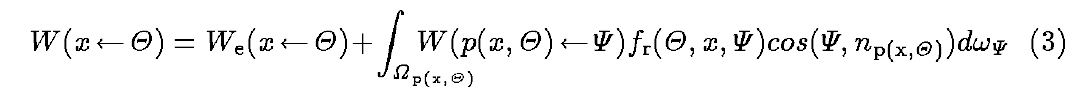
  • shooting process
    • 算法从光源开始出发，一直追光线，直到 pixel
  • 问题：很难追到相机

The Next Event Estimator

  • NEE：直接连 pixel