(论文)[1900-SIG-C] Particle Transport and Image Synthesis

Particle Transport and Image Synthesis

• 论文

Abstract

• The rendering equation is similar to the linear Boltzmann equation which has been widely studied in physics and nuclear engineering.
• 可以参考其他领域的方法，引入 RR/S

Introduction

• render equation
  • radiosity
  • ray tracing
• distributed ray tracing
  • 能做一些其他的效果：景深、半影、运动模糊、模糊反射
  • TODO

Particle Transport

• equation
  • \(K\)：scattering kernel

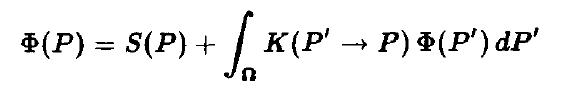
• 拆分光路：不同的模式给不同的渲染方式（radiosity、pt）

Russian Roulette

• 传统光路停止条件
  • albedo=0
  • 打空
• 可能会出现浪费大量时间在追踪低贡献的长光路上
  • bias solution
    • weight cutoff：低于阈值的时候截断（返回 0）
    • adaptive tree depth control
  • unbiased solution
    • Russian Roulette
• 期望权重：\(P\) 表示停止的概率

• 算法

• RR 必然增大方差

Splitting-Paths vs Trees

• S 必然减小方差
• 效率（efficiency）：方差、开销乘积倒数

\[ \epsilon=\dfrac{1}{\sigma^2\tau} \]

• splitting 在某些情况下能让效率提升
• \(N\) 次镜面反射，之后碰到漫反射表面
  • \(\tau\)：漫反射表面的开销

\[ \epsilon_{1}=\dfrac{1}{\sigma_{1}^2(N\alpha+\tau)} \]

• splitting：\(m\)

\[ \epsilon_{m}=\dfrac{1}{\sigma_{m}^2(N\alpha+m\tau)},\sigma_{m}<\sigma_{1} \]

• \(N\to\infty\)

\[ \lim_{N\to\infty}\dfrac{\epsilon_{m}}{\epsilon_{1}}=\dfrac{\sigma_{1}}{\sigma_{m}}>1 \]

• 因此当 \(N\) 足够大的时候（存在 \(N\)），splitting 效率高
• 分层采样
  • 划分，每个划分内部独立采样（采样分布为原始的采样分布在区域中的归一化）
• 如果光线的入射方向（光源）能够划分为若干个区域（划分），这些区域内部的方差小的话，此时往不同的区域中各发射一条光线效率高
  • 直接光照、间接光照