(论文)[2023-SIGC] Neural Parametric Mixtures for Path Guiding

Posted on Edited on In Views:
使用 VMM 表示用于采样的 pdf，使用神经网络估计 VMM 的参数

NPM

  • Neural Parametric Mixtures for Path Guiding
  • SIGGRAPH 2022
  • 主页

摘要

  • NPM：神经网络隐式表示 PG 使用的 pdf

introduction

  • 之前的 PG 方法一般不能很好的构建 spatial-directional 之间的相关性
    • 离散化的问题

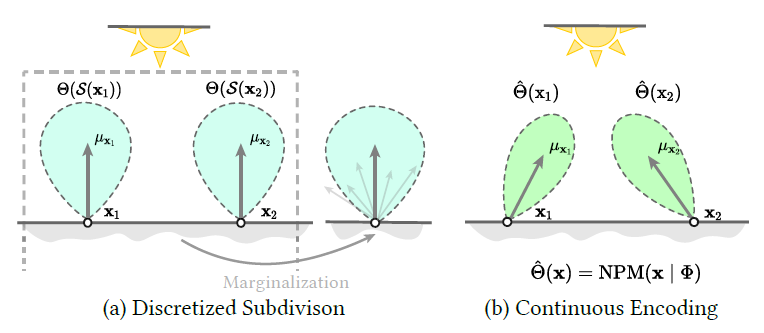
  • 之前的方法，需要大量训练得到 spatial/directional 合适的细分程度
  • NPM
    • 一个方便学习 + 采样的分布，快速学习（SGD 就行），lightweight MLP
    • 连续建模
    • GPU
    • 可以直接学习 BSDF x L 的结果
  • Path Guiding
  • Parametric Mixture Models
    • 比较好的特性
      • closed-form solutions for products, convolutions and integrals
      • 采样快
    • Gaussian mixtures
    • von Mises-Fisher mixtures
  • Implicit Neural Representation
    • NeRF

preliminary

  • 渲染方程：\(\omega_o\) 表示 camera rays 的方向

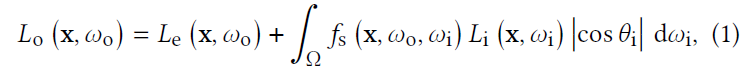
  • \(N=1\) 样本 MC 无偏估计

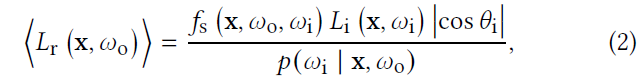
  • Von Mises-Fisher（vMF）
    • 方向：\(\mu\in\mathbb{S}^2\)
    • sharpness：\(\kappa\in[0,+\infty]\)

\[ v(\omega\mid\mu,\kappa)=\dfrac{\kappa}{4\pi\sinh\kappa}\exp\left(\kappa\mu^{T}\omega\right) \]

  • VMM 是 vMF 的加权混合（\(\lambda_i\)）

\[ \mathcal{V}(\omega\mid\Theta)=\sum_{i=1}^{K}\lambda_i\cdot v_i(\omega\mid\mu_i,\kappa_i) \]

  • VMM 的优势
    • fewer parameters (4 floats per component)
    • efficient importance sampling
    • closed-form product and integration

NPM

  • pipeline

Radiance-based NPM

  • NPM 想要实现的目标

\[ \mathcal{V}(\omega_i\mid\Theta(\mathrm{x}))\propto L_{\text{i}}(\mathrm{x},\omega_i) \]

  • NPM 将输入解码成 VMM 的参数 \(\hat{\Theta}(\mathrm{x})\)，用于采样
    • \(\Phi\) 表示 MLP 中待学习的参数

\[ \text{NPM}_{\text{radiance}}(\mathrm{x}\mid\Phi)=\hat{\Theta}(\mathrm{x}) \]

  • 为了保证网络输出的参数满足 vMF 的要求，对网络输出做一个映射
    • 加了激活函数

\[ \lambda_i,\kappa_i>0,\mu_i\in\mathbb{S}^2,\sum_{i=1}^{K}\lambda_i=1 \]

  • 网络：最直观的方式就是直接使用 MLP：\(\mathrm{x}\to\hat{\Theta}\)
    • 一个简单的神经网络无法模拟高频信息，因此 NPM 加上了一个 trainable multi-resolution spatial embedding

Optimizing NPM

  • SGD
  • \(\Theta_{\text{gt}}(\mathrm{x})\) 是未知的
  • 之前的算法：EM（不适用于隐式的方法）
  • 将真实分布 \(\mathcal{D}\) 和我们学习的分布 \(\mathcal{V}\) 之间的 KL 散度作为 loss
  • 给定位置 \(\mathrm{x}\)，loss 如下

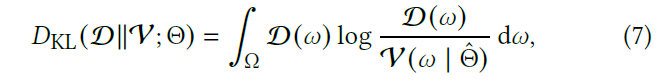
  • 在 radiance-based PG 中，\(\mathcal{D}\propto L_i\)
    • 在实际实现中，我们直接使用 \(L_i\)
    • 使用 \(k\mathcal{D}\) 还是 \(\mathcal{D}\) 不影响最值
  • loss 没法直接得到，使用 MC 估计
    • \(N\) samples
    • \(\tilde{p}\)：采样分布，我们使用 BSDF 和 VMM 的 MIS

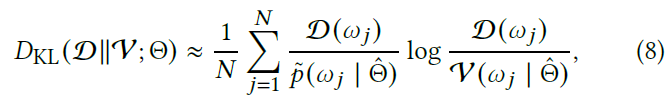\[ D_{\text{KL}}(\mathcal{D}\|\mathcal{V};\Theta)\approx\dfrac{1}{N}\sum_{j=1}^{N}\dfrac{\mathcal{D}(\omega_j)}{\text{sg}\left(\tilde{p}(\omega_j\mid\hat{\Theta})\right)}\log\dfrac{\mathcal{D}(\omega_j)}{\mathcal{V}(\omega_j\mid\hat{\Theta})} \]

  • 在计算的时候，可以把 loss 中的常数部分去掉【不产生梯度，论文实现就是这样】

\[ D_{\text{KL}}(\mathcal{D}\|\mathcal{V};\Theta)\approx-\dfrac{1}{N}\sum_{j=1}^{N}\dfrac{\mathcal{D}(\omega_j)}{\text{sg}\left(\tilde{p}(\omega_j\mid\hat{\Theta})\right)}\log\mathcal{V}(\omega_j\mid\hat{\Theta}) \]

  • loss 到参数的梯度（用于训练）如下
    • 另外可以过滤 \(\mathcal{D}=0\) 的样本，也不产生出梯度，大大提高训练速度

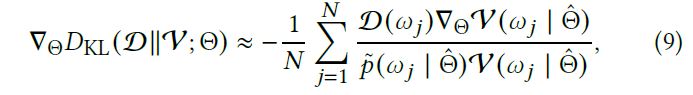
  • 实际训练对：\((\mathrm{x},\omega_i)\to L_i\) 分布在不同的空间位置，需要在每个位置都收敛
  • 我们希望得到的最优 \(\Phi\)，满足

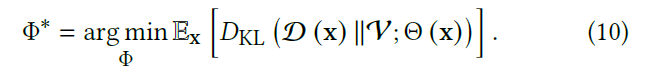
  • adaptive training：梯度最大的地方，loss 最大（占主导）

Full Integrand Learning

  • 需要考虑 \(\omega_o\)，对于神经网络来说很自然，能够表示就能够学习

\[ \text{NPM}_{\text{product}}(\mathrm{x},\omega_o\mid\Phi)=\hat{\Theta}(\mathrm{x},\omega_o) \]

  • 想要训练的目标变成

\[ \mathcal{V}(\omega_i\mid\hat{\Theta}(\mathrm{x},\omega_o))\propto f_{\text{s}}(\mathrm{x},\omega_o,\omega_i)L_{\text{i}}(\mathrm{x},\omega_i)\left\vert\cos\theta_i\right\vert \]

  • 其中 \(\cos\) 可以使用一个 constant vMF 来表示

其他

  • Auxiliary Feature Inputs（去掉效果掉的不多）
    • surface normal \(\mathrm{n}(\mathrm{x})\) and roughness
  • Input Encoding
    • 模拟 non-linearity between multidimensional inputs and outputs
      • trainable multi-resolution spatial embedding
      • 和 NRC 一样
    • \(\omega_{\text{o}},\mathrm{n}(\mathrm{x})\)：spherical harmonics
      • NeRF

实现

Multi-resolution Spatial Embedding

  • 映射：\(\mathrm{x}\to\hat{\Theta}\)（radiance-based version）
    • \(\mathbb{R}^3\to\mathbb{R}^{4\times K}\)
  • 直接使用 MLP，很难建模空间上的高频变化
  • 使用可学习的多分辨率的空间编码
  • \(L\) 个 3D 均匀网格 \(G_1,\cdots,G_l,\cdots G_L\)
    • 每一个都覆盖整个空间
    • 每一个的空间分辨率为 \(D_l^3\)（成倍增加）
    • 每一个网格位置定义一个 latent feature vector \(v\in \mathbb{R}^{f}\)
      • 非格点位置，线性插值

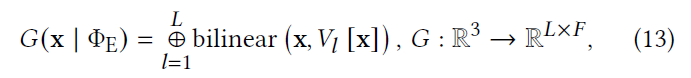
  • \(V_l[\mathrm{x}]\)：对应的用于插值的 8 个位置的 latent vector
  • radiance-based NPM 现在变成如下形式
    • \(\Phi_{\text{E}}\)：spatial embedding
    • \(\Phi_{\text{M}}\)：MLP

\[ \text{NPM}_{\text{radiance}}\left(G(\mathrm{x}\mid\Phi_{\text{E}})\mid\Phi_{\text{M}}\right)=\hat{\Theta}(\mathrm{x}) \]

Online Training Scheme

  • Optix + GPU，wavefront
  • structure-of-arrays (SoA) memory layout
  • Training Scheme
    • 边训练，边渲染
    • 固定比例的 budget(spp/time) 用于渲染
      • 实验：\(25\%\)
    • NPM 在 150spp（15s，1000 training step）便能够收敛

Guiding Network

  • tiny-cuda-nn
  • MLP
    • 3 linear layers of width 64
    • ReLU activation（最后一层使用表格中的激活函数）
  • VMM：8 vMF（\(K=8\)）
  • Grid Embembbing：\(L=8\)
    • increasing resolutions：\(D_1=8,D_8=68\)
    • feature：\(F=4\) floats
  • training
    • \(\text{lr}=0.005\)
    • Adaptive momentum techniques（Adam）
    • vMF 采样
  • inference
    • EMA（NRC 相似）

结果讨论

  • RTX3070
  • 不开 NEE、RR，最大深度 10
  • 720p
  • metric：relMSE、MAPE、MRSE
  • MIS：（fixed）50% BSDF + 50% Method

对比

  • 在训练早期，结果就已经比较好了
    • 黄色的是 PT

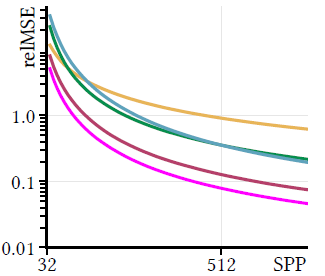
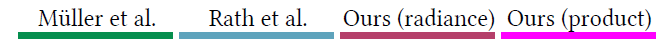
  • 和 Rath 的 VAPG 相比，又快又好
    • 和 PPG 相比，平均有 1.5x 的加速

Evaluation

  • Trainable Spatial Embedding
    • No Encoding ~ Frequency < Single-Resolution < Multi-Resolution
  • Training Efficiency
    • 少量样本的时候，效果就已经比较好了（> VAPG）

Discussion

  • Path Guiding Extensions
    • 学习 MIS 的采样概率（论文固定 50%）
    • VAPG 中的理论：学 \(L_i^2\)
  • Performance Analysis
    • 720p 过一遍网络：3ms
    • training step（\(2^{18}\) samples）：10ms
    • 2M params：<10 MB 内存
  • Alternative Solutions
    • 其他方法复杂，不适合 GPU

Future

  • 更好的基函数
    • VMM 数量固定，表达不够准确