(论文)[1997-EGSR] An Error Metric for Monte Carlo Ray Tracing

Posted on Edited on In Views:
Russian Roulette 和 Splitting 的方差分析，最优化 RR+S 方差分析，利用预追踪一些光线，计算得到一些统计量，用这些统计量指导实际光追时获取最优的 RR/S 值

An Error Metric for Monte Carlo Ray Tracing

  • Mark R. Bolin Gary W. Meyer

Introduction

  • 提出了一种标准，用于衡量蒙特卡洛光线追踪的误差
  • visual system 中的误差（传输、显示）
    • 量化误差，压缩算法带来的误差
    • 噪声
  • 因此考虑到效率的因素，我们需要知道误差界，从而更好的选择 spp 数

Previous work

  • Kajiya [1986]：The Rendering Equation
    • 渲染方程
    • ray trees 是低效的，大部分贡献不高
    • 提出了 path tracing 的框架
  • Kirk [1990-SIG]：Particle Transport and Image Synthesis
    • Russian Roulette：当权重小于一个阈值时使用
    • Splitting：未给出使用的指导
  • Arvo [1994]：A Framework for the Analysis of Error in Global Illumination Algorithms
    • 误差评估，主要集中在辐射度算法
  • Lee [1985]：Statistically Optimized Sampling for Distributed Ray Tracing
    • 在 image plane 中分析，在给定阈值下，需要多少 spp 数
    • TODO

Error of Monte Carlo simulations

1个交点一条光线

  • MC 估计

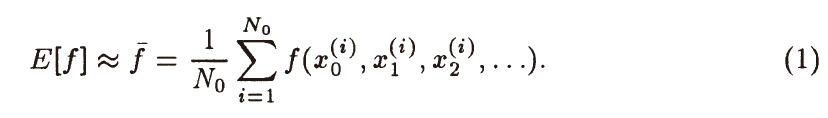
  • 函数的方差（函数本身性质，和样本数无关）

\[ V\left[f\right]=E\left[f^2\right]-E^2\left[f\right] \]

  • MC 估计的方差
    • 两个方差的区别，详细看这里

\[ V\left[\bar{f}\right]=\dfrac{V\left[f\right]}{N_0} \]

  • 此时，如果期望准确率 \(V_d\left[\bar{f}\right]\)，函数方差 \(V\left[f\right]\)，则需要的样本数 \(N_0\)

\[ N_0=\dfrac{V\left[f\right]}{V\left[\bar{f}\right]} \]

1个交点多条光线

条件期望公式

  • 重期望公式

\[ E[X]=E_Y[E_X[X\mid Y]] \]

  • 条件期望公式

\[ \begin{aligned} V[X] &=V[E[X\mid Y]]+E[V[X\mid Y]]\\ &=V_Y[E_X[X\mid Y]]+E_Y[V_X[X\mid Y]] \end{aligned} \]

  • 推导

\[ \begin{aligned} V_X[X\mid Y] &=E_X\left[[X-E[X]]^2\mid Y\right]\\ &=E_X\left[X^2\mid Y\right]-E_X^2[X\mid Y] \end{aligned} \]

\[ \begin{aligned} V_Y[E_X[X\mid Y]] &=E_Y\left[\left(E_X[X\mid Y]-E_X[X\mid Y]\right)^2\right]\\ &=E_Y\left[E_X^2[X\mid Y]\right]-E_Y^2\left[E_X[X\mid Y]\right]\\ &=E_Y\left[E_X^2[X\mid Y]\right]-E^2[X]\\ \end{aligned} \]

\[ \begin{aligned} E_Y[V_X[X\mid Y]] &=E_Y\left[E_X\left[X^2\mid Y\right]-E_X^2[X\mid Y]\right]\\ &=E_Y\left[E_X\left[X^2\mid Y\right]\right]-E_Y\left[E_X^2[X\mid Y]\right]\\ &=E[X^2]-E_Y\left[E_X^2[X\mid Y]\right]\\ \end{aligned} \]

  • 于是有

\[ \begin{aligned} V_Y[E_X[X\mid Y]]+E_Y[V_X[X\mid Y]] &=E[X^2]-E^2[X]\\ &=V[X]\\ \end{aligned} \]

ray tree

  • 根据 level 展开，得到如下式子

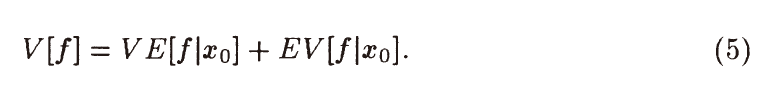
  • 递归展开

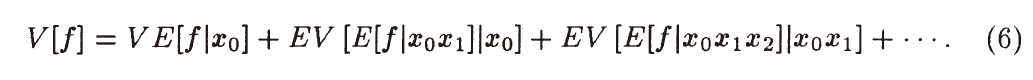
  • 递归示例

\[ \begin{aligned} V[f] &=V[E[f\mid x_0]]+{\color{red}E[V[f\mid x_0]]}\\ &=V[E[f\mid x_0]]+E\Big[V[E[f\mid x_0x_1]\mid x_0]+E[V[f\mid x_0x_1]\mid x_0]\Big]\\ &=V[E[f\mid x_0]]+E[V[E[f\mid x_0x_1]\mid x_0]]+E[E[V[f\mid x_0x_1]\mid x_0]]\\ &=V[E[f\mid x_0]]+E[V[E[f\mid x_0x_1]\mid x_0]]+E[V[f\mid x_0x_1]\mid x_0x_1]\\ &=VE[f\mid x_0]+EV[E[[f\mid x_0x_1]\mid x_0]]+{\color{red}EV[f\mid x_0x_1]}\\ &=\cdots \end{aligned} \]

  • 每次展开，多一项，即每一个 ray tree 节点引入的方差
    • 也就是说，全局的方差就来自于每一个 ray tree 节点引入的方差

\[ EV[E[[f\mid x_0\cdots x_L]\mid x_0\cdots x_{L-1}]] \]

Splitting

  • ray tree 中每一个节点分裂不止一条光线
  • 例如：\(x_0\) 出采样多个出射方向（多个 \(x_1\) ）

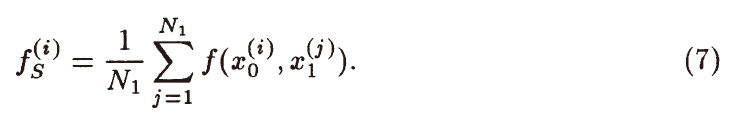
  • 方差

  • 和式子 5 相比，方差减小如下

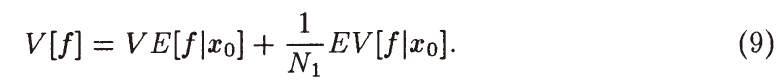\[ \begin{aligned} V[f_\text{S}] &=VE[f_\text{S}\mid x_0]+EV[f_\text{S}\mid x_0]\\ &=VE[f\mid x_0]+\dfrac{1}{N_1}EV[f\mid x_{0}]\\ &=V[f]+\dfrac{1-N_1}{N_1}EV[f\mid x_{0}] \end{aligned} \]

  • 但是因为增加了额外的计算开销（发射额外的光线），因此只有 \(EV\) 项比 \(VE\) 项大时效果才比较好

Russian Roulette

  • 提前终止不重要的光线

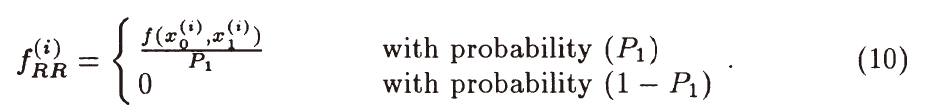
  • 期望
    • 式子中的 \(f\equiv f\mid x_0,f_{RR}\equiv f_{RR}\mid x_0\)

\[ E[f_{RR}]=P_1E\left[\dfrac{f}{P_1}\right]+(1-P_1)\cdot0=E[f] \]

  • 方差如下

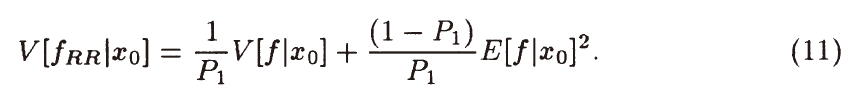
  • 推导如下
    • 式子中的 \(f\equiv f\mid x_0,f_{RR}\equiv f_{RR}\mid x_0\)

\[ \begin{aligned} V[f_{RR}] &=P_1E\left[\dfrac{f}{P_1}-E[f_{RR}]\right]^2+(1-P_1)E\Big[0-E[f_{RR}]\Big]^2\\ &=\dfrac{1}{P_1}E\Big[f-P_1E[f]\Big]^2+(1-P_1)E^2[f]\\ &=\dfrac{1}{P_1}\Big(E[f^2]+(P_1^2-2P_1)E^2[f]\Big)+(1-P_1)E^2[f]\\ &=\dfrac{1}{P_1}\Big(E[f^2]-E^2[f]+(1+P_1^2-2P_1)E^2[f]\Big)+(1-P_1)E^2[f]\\ &=\dfrac{1}{P_1}V[f]+\dfrac{(1-P_1)P_1+(1-P_1)^2}{P_1}E^2[f]\\ (结果)&=\dfrac{1}{P_1}V[f]+\dfrac{(1-P_1)}{P_1}E^2[f]\\ &=\dfrac{1}{P_1}\left(V[f]+E^2[f]\right)-E^2[f]\\ &=\dfrac{1}{P_1}E[f^2]-E^2[f]\\ &=\dfrac{1-P_1}{P_1}E[f^2]+V[f]\\ \end{aligned} \]

  • 和式子 5 相比，方差增大如下
  • RR 必然增大方差

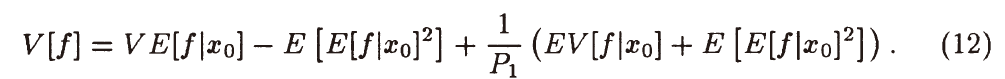\[ \begin{aligned} V[f_\text{RR}] &=VE[f_\text{RR}\mid x_0]+EV[f_\text{RR}\mid x_0]\\ &=VE[f\mid x_0]+EV[f\mid x_0]+\dfrac{1-P_1}{P_1}\left(EV[f\mid x_0]+E[E^2[f\mid x_0]]\right)\\ &=VE[f\mid x_0]+EV[f\mid x_0]+\dfrac{1-P_1}{P_1}\left(EE[f^2\mid x_0]\right)\\ &=V[f]+\dfrac{1-P_1}{P_1}\left(EE[f^2\mid x_0]\right) \end{aligned} \]

  • 但是因为减少计算开销（发射的光线变少了），因此只有 \(EV\) 项和 \(EE\) 项比 \(VE\) 项小时效果才比较好

一般情况

  • RR+S
    • S 比较简单，直接除以数量即可
    • RR 比较复杂，分类讨论
  • 方差，综合式子 \((5)(8)(11)\)
  • \(N_L\)：RR概率 / 分裂数目

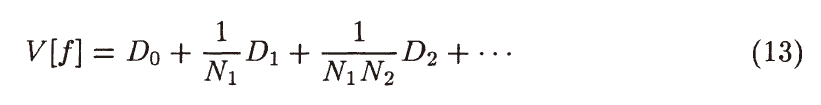
  • \(D_L\)

Optimum splitting and Russian Roulette

  • 之前的工作：ad-hoc（scene-specific）
    • RR：N bounce && weight 降低到一定值之后
    • S：固定设置为 1（PT） or N
  • quality

\[ Q=cost\times V[f] \]

  • 通过光线数目来衡量，cost 可以被表示为

  • 求解最优的 \(N_L\)：\(\dfrac{\partial Q}{\partial N_L}=0\)

\[ N_L=\sqrt{\dfrac{D_L}{D_{L-1}}}\quad\quad(16) \]

证明

  • 把无关项写到一起

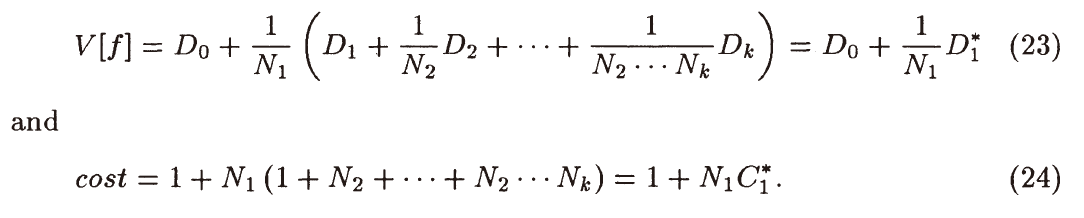
  • 最小化 \(Q\)

  • 代回 \(Q\)

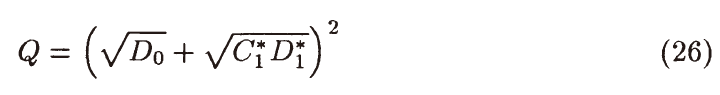
  • 此时 \(C_1^{\ast}Q_1^{\ast}\) 最小，则 \(Q\) 最小
    • 同理需要 \(C_L^{\ast}Q_L^{\ast}\) 最小
  • 根据 \((25)(23)\) 得到

\[ D_0=\dfrac{V[f]}{cost} \]

  • 此时观察 \((23)(24)\)，可以得到 \((16)\) 的结果

\[ N_L=\sqrt{\dfrac{D_L}{D_{L-1}}} \]

  • \(L=1\) 显然， \(L>1\) 类似的方法推导即可

使用

  • 最优的 \(N_L\) 不好应用，因为 \(D_{L-1}/D_L\) 依赖于 \(\text{level}=L-1,L+1\) 是否 RR
    • \(L+1\) 未知，这个本身就是我们计算的问题（循环依赖）
  • trick：假设成立，验证是否可行，可行则继续，不可行则回退
    • \(\text{level}=1\) 开始
    • 每一个 level，我们都假设在 \(L,L+1\) 都使用 RR
      • 如果计算得到的 \(N_L<1\)，则进入 \(L+1\)（可能符合我们的假设）
      • 如果 \(N_L\ge1\)，和假设不符，此时 \(L\) 不使用 RR（与预期不符），回退 \(L-1\)，重新计算最优的 \(N_{L-1}\)
        • 如果 \(N_{L-1}\) 之前 \(<1\)，现在 \(\ge1\)，还需要继续回退
        • 否则进入 \(L\)，重新计算 \(N_L\)

Terminations

  • 提前结束：击中光源、打空
    • 很常见
  • 考虑提前终止的影响
  • \(L-1\) 停止的光线不会影响 \(L\) 的方差，因此只有到达 \(L\) 的占比 \(R_L\) （到达 \(L\)）的光线会带来方差
  • 因此有
    • \(EV\) 只考虑能够到达 \(1\) 的光线

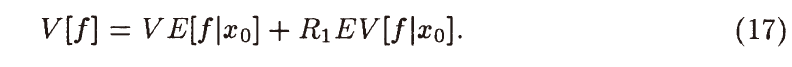
  • \(R\) 这一项的含义：所有的方差分析建立在能够到达 \(L\) 的光线
  • 推导：\(t\) 表示停止，\(c\) 表示继续

\[ \begin{aligned} V[f]&\\ (分段积分)&=V_{t}[f]+V_{c}[f]\\ &=V_tE[f\mid x_0]+E_tV[f\mid x_0]+V_cE[f\mid x_0]+E_cV[f\mid x_0]\\ &=V_tE[f\mid x_0]+0+V_cE[f\mid x_0]+E_cV[f\mid x_0]\\ &=V_tE[f\mid x_0]+V_cE[f\mid x_0]+E_cV[f\mid x_0]\\ &=VE[f\mid x_0]+E_cV[f\mid x_0]\\ \end{aligned} \]

  • 更新 RR、S
    • 综合式子 \((8)(11)(17)\)

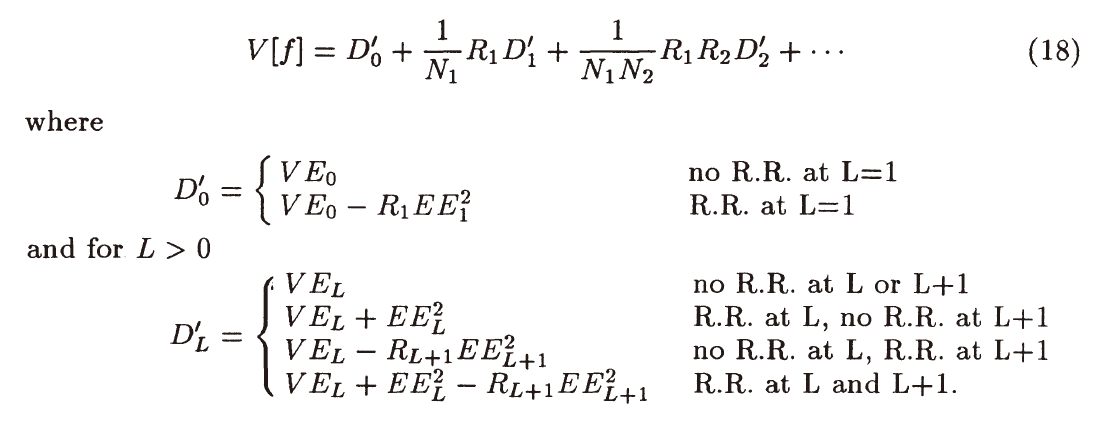
  • 这里的 \(VE_L,EE_L^2\) 只计算到达 \(L\) 的光线
  • cost 更新

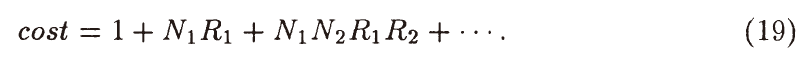
  • 最优结果
    • 分母重用之前的表达，但是只考虑能够到达 \(L\) 的光线

Implementation

  • 实现上为了计算 \(D\)，需要预先采样样本计算一些期望和方差
  • 算法思路
    • 预先采样 pilot samples，估计 \(D\) 以及 \(N_L\)
    • image plane 的防擦好被计算得到
    • 根据要求的精度，为每一个像素计算 spp
  • 输入
    • pilot sampling rate
    • target variance within the image plane
  • 为了估计方差，在每一个交点都需要发射若干光线
    • 实现上，随着深度增加可以减少样本数
  • 计算顺序
    • 每一个 level 都能采样，此时能够计算
      • \(V[f]\)：像素
      • \(V[f\mid x_0\cdots x_{L-1}],E^2[f\mid x_0\cdots x_{L-1}]\)：level \(L\)
    • 根据上面的值计算 \(E\big[V[f\mid x_0\cdots x_{L-1}]\big],E\big[E^2[f\mid x_0\cdots x_{L-1}]\big]\)
    • 同时可以光线数目估计 \(R_L\)
    • 都算完了，根据式子 9，计算 \(VE\) 项

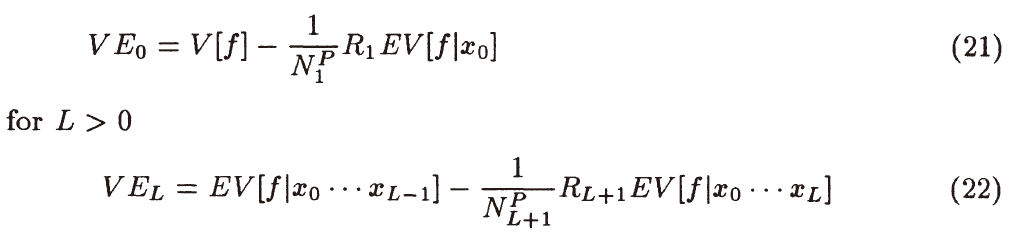
  • 最后可以估计 \(N_L\) 了
  • 这个方法计算代价很高，因为需要大量的 pilot samples