(论文)[2020-TOG] Variance-Aware Path Guiding
Variance-Aware Path Guiding
- 找到了一个更好的 pdf,同时往方差更大的方向发射更多的光线
- 考虑 path guiding 过程中 \(\langle{L_i}\rangle\) 本身的估计方差
- ALEXANDER RATH, DFKI and Saarland University, Germany
2. PREVIOUS WORK
- Path tracing:BSDF Important Sampling、NEE
- Bidirectional methods:BDPT、PM
- less efficient:large scenes with many light sources
- Local path guiding
- 数据结构
- histograms based on a photon map
- tree structures
- particle footprints
- parametric mixture models
- neural networks
- 近似项
- incident radiance field \(L_i\)
- product:\(L_i\) with BSDF
- 可以扩展到 participating media
- 数据结构
- Light selection:hemispherical
distribution
- path guiding 学习直接光照
- Global path guiding
- sampling paths similar to a set of previously selected guiding paths
- guiding in primary sample space
- Metropolis light transport:MCMC
- 变异路径相关性大,容易陷入局部极值
- visible artefacts、poor temporal coherence
- 在双向方法中表现不错,camera paths 使用 PT 追出来,相关性问题有所缓解
- Target densities
- MC 方法收敛到容易得到的 target function(不同于被积分项),用于采样(感觉就是 pdf)
- 其他方式:不是学
pdf,而是其他东西
- NEE 的时候如何对多光源进行重要性采样
- how a given target density can be optimally approximated
3. BACKGROUND
- 渲染方程
\[ L_{o}(\omega_{o},x)=L_{e}(\omega_{o},x)+\int_{\Omega} L_{i}( \omega_{i},x) B(\omega_{o}, x, \omega_{i})\vert{\cos\theta_i}\vert\;\mathrm{d} \omega_{i} \]
- 蒙特卡洛积分
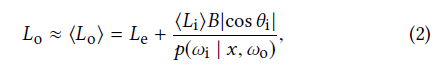
- 方差(Estimation error)
- zero-variance:采样 PDF 正比于被积分项
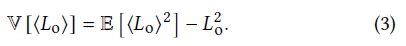
4 TARGET DENSITIES FOR LOCAL PATH GUIDING
- 首先假设只有中间一个点 \(x\) 能被 guiding
4.1 Adaptive densities-The irradiance integral
- 近似目标(diffuse):此时不同方向上的 radiance 相同,因此只需要考虑
irradiance 即可
- 系数无所谓
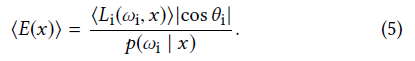
- estimator
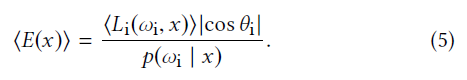
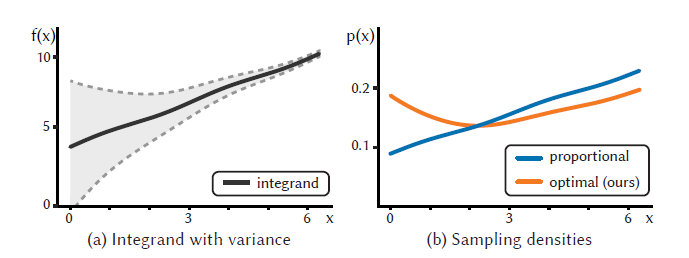
- 假定:\(w_i\) 只采样一个出射方向,\(L_i\) 通过嵌套的 MC 方法估计
- 之前的工作,找到最优 \(p\),这样的方式忽略了 \(\langle{L_i}\rangle\) 内部的方差
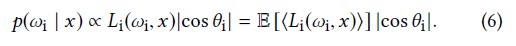
- 直观:方差大的地方需要更多的样本
- 浅灰色区域:越宽表示方差越大
- 按照之前的方式效果不好
- 论文观点
- 之前的方法都是让 PDF 正比于被积分项,我们提出需要让整体的方差最小
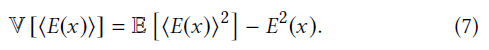
- 第二项为常数,只需要考虑第一项
- 二阶矩是凸函数,因此可以用拉格朗日乘子法优化
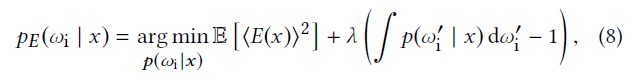
- 最优的结果如下
\[ p_E(\omega_i|x)\propto \sqrt{\mathbb{E}\left[\left\langle{L_i(\omega_i, x)}\right\rangle^2\right]}\left\vert\cos(\theta_i)\right\vert \]
- 计算过程:对 \(p(\omega_i),\lambda\) 求偏导为 \(0\),结果正比于上面这一项
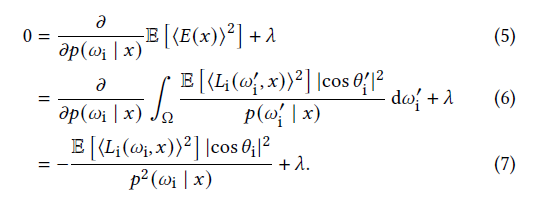
- 简单的来说,泛函的导数定义如下
\[ f(p+\delta{p})=f(p)+\langle{f'(p),f(\delta{p})}\rangle+o(\delta{p}) \]
- 泛函的内积定义为
\[ \langle{p(x),q(x)}\rangle=\int{p(x)q(x)\;\mathrm{d}x} \]
- 按照定义展开之后,可以得到上面的结果
- 如果 \(\langle{L_i}\rangle\) 的估计没有误差(方差为 0),此时和之前的方法一样
\[ \mathbb{E}\left[\langle{L_i}\rangle^2\right]=L_i^2 \]
场景设定
- 光源:environment map
- a small, strong sun
- a uniform sky
- Guiding 的数据结构建立在纯 diffuse
的地面上,墙面是纯玻璃(纯反射/折射)
- 光只来源于两个方向:直接、玻璃反射(玻璃折射则失效)
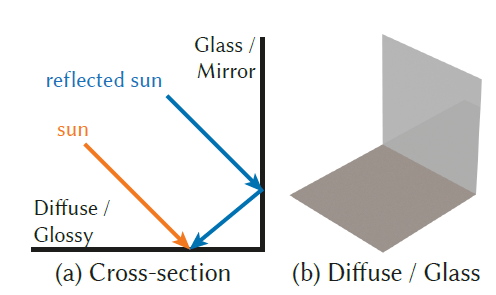
- 玻璃反射处贡献高,同时方差大,论文方法能够以打出更多光线
- 方差大:折射则贡献为 0,反射则贡献很大

4.2 Marginalized product sampling
- 待估计的式子如下,7D 太复杂,不考虑 \(\omega_o\)
- marginalized over the outgoing direction
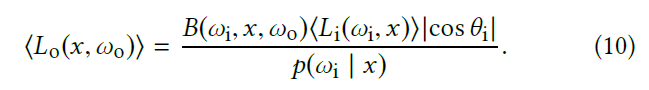
- 类似的,让方差最小化
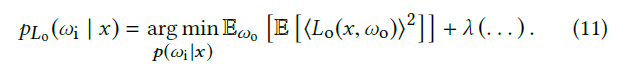
- 我们可以得到如下式子
\[ p_{L_o}(\omega_i|x)\propto \sqrt{\mathbb{E}\left[B^2(\omega_i,x,\omega_o)\left\langle{L_i(\omega_i, x)}\right\rangle^2\right]}\left\vert\cos(\theta_i)\right\vert\quad\quad(12) \]
- 过程如下
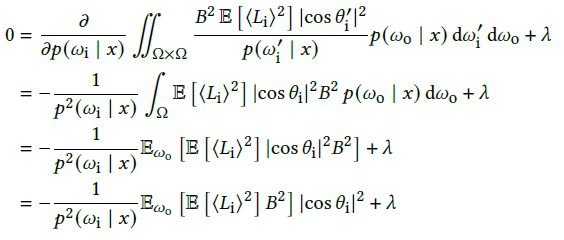
- 当 \(\omega_i,x,\omega_o\) 都固定的时候,如下式子成立
\[ \begin{aligned} \mathbb{E}\left[\langle{L_o(x,\omega_o)}\rangle^2\right] =&\mathbb{E}\left[\dfrac{L_{i}^2( \omega_{i},x) B^2(\omega_{o}, x, \omega_{i})\vert{\cos\theta_i}\vert^2}{p^2(\omega_i\vert x)}\right]\\ \\ =&\mathbb{E}\left[L_{i}^2( \omega_{i},x)\right] \cdot\dfrac{B^2(\omega_{o}, x, \omega_{i})\vert{\cos\theta_i}\vert^2}{p^2(\omega_i\vert x)} \end{aligned} \]
- 场景设定:地板设置为 glossy,墙面还是纯玻璃

- 环境光部分的重视程度变高了
- 对比算法不考虑 BSDF,和 4.1 用的一样,结果也和 4.1 类似(应该说是一样,正比)
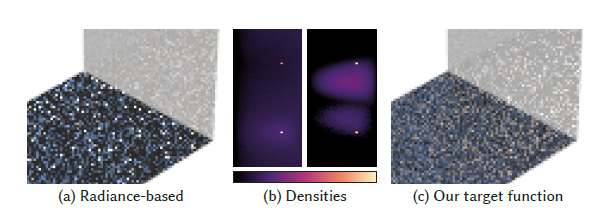
- 结论:上面这种方式在我们设定的优化目标下是最优的,但并不是全局最优的,原因如下
- 一些 glossy 还是直接通过 BSDF importance sampling 更好,例如 almost specular reflections
- 我们优化目标是 most frequent directions,这不一定是 most important directions
4.3 Minimizing the image error
- 理论上最好的 target density 需要使得每一个像素的方差最小
Pixel contribution
- 考虑场景中的一个点 \(x\) 对像素 \(px\) 的贡献
![]()
- \(\bar{x}\):所有可能的光路
- \(f_{px}(\cdot)\):贡献函数
- 乘积:sensor response、path throughput
- \(P_x\):所有 \(\bar{x}\) 组成的路径子空间
- \(L_o(x)\) 项更标准一点感觉应该写成 \(L_o(\bar{x})\),因为和方向相关
Minimizing the pixel error
- 采样 \(\bar{x}\),二级矩估计
![]()
- 如何得到上面的式子采样过程:\(p(\bar{x})p(\omega_i\vert x)\)
- 只有在最后一个点上使用 path guiding
- 考虑光线不分裂,一次只采样一条光线(guiding
的时候只采样一条光线),否则应该是 \(\langle{L_o(x)}\rangle^2\) 而不是 \(\langle{L_o(x)}\rangle\) 中各项的平方点积
- 是和的平方而不是平方的和
- 最优的 \(p\) 如下,和 4.2 类似,与 \(p\) 无关的量都看成不变的即可
![]()
Minimizing the MSE of the image
- 让整张图片的 MSE 最小,对所有像素求和,修改的是拉格朗日算子,最小化如下式子
\[ \sum_{px}\mathbb{E}\left[\langle{C_{px}}(x)\rangle^2\right]+\lambda(\dots) \]
- 最优 \(p\) 如下,就是个求和
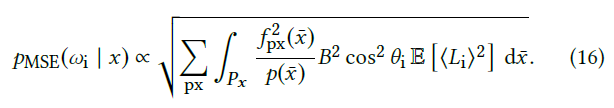
- MSE:会更加重视亮的区域而忽视暗的区域
- relMSE:除以像素值,相当于 \(C_{\text{px}}(x)\) 除以 \(I_{\text{px}}\)
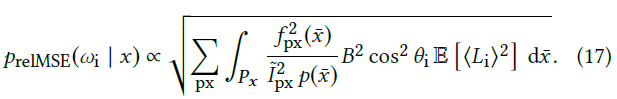
- \(I_{\text{px}}\)
不知道,可以使用之前迭代轮的结果降噪之后的结果 \(\tilde{I}_{\text{px}}\) 作为真值(怪)
- 避免除 0,偏移 \(\epsilon\)
4.4 Spatial caches
- path guiding 中不会保存所有点的分布,而是一个区域 \(S\)(cell / treenode)
- \(x\in S\)
- 问题:只有对少数点来说重要的方向被掩盖,导致少数点方差极大
- 只考虑 irradiance,优化方程和结果如下
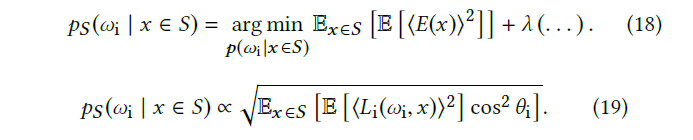
- 直观上,根号操作放到了最后,能够让边界变化更快
\[ \sum{\dfrac{L_i}{N}}\le\sqrt{\sum{\dfrac{L_i^2}{N}}} \]
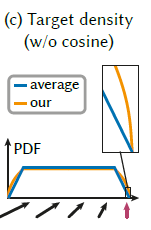
- 其他两种分析也类似
- simple:simple BSDF marginalization
- full:relMSE
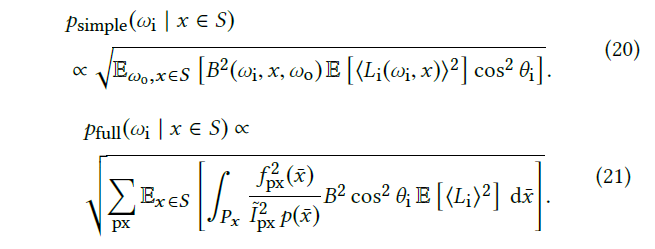
5 MULTIPLE IMPORTANCE SAMPLING
- 只是用学出来的策略可能会带来:excessive variance, bias, ...
- 问题来源:学不准(因此一般会和 BSDF 重要性采样结合一下)
- simplification of the integrand
- neglect the BSDF
- marginalization over important terms
- outgoing direction or surface normal
- noisy "ground truth"
- simplification of the integrand
- estimator:one-sample MIS with the balance heuristic
- \(p_g\):学到的分布
- \(p_B\):BSDF
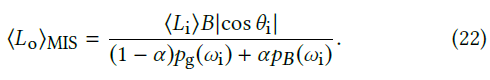
- 对于任意 \(w\) 的两种方式的
MIS,拆分如下
- 注意这里的 \(\alpha\) 依赖于 \(x,\omega_o\)
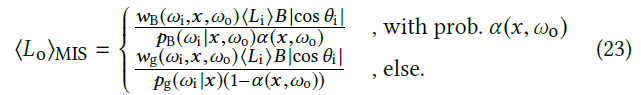
- 这里的写法和之前这里的写法不太一样,是下面式子最后一行的写法
\[ \begin{aligned} F &=\sum_{i=1}^{n}\dfrac{1}{n_i}\sum_{j=1}^{n_i}w_{i}(X_{i,j})\dfrac{f(X_{i,j})}{p_i(X_{i,j})}\\ &=\sum_{i=1}^{n}\dfrac{1}{N}\cdot\dfrac{N}{n_i}\sum_{j=1}^{n_i}w_{i}(X_{i,j})\dfrac{f(X_{i,j})}{p_i(X_{i,j})}\\ &=\dfrac{1}{N}\sum_{i=1}^{n}\sum_{j=1}^{n_i}w_{i}(X_{i,j})\dfrac{f(X_{i,j})}{c_ip_i(X_{i,j})}\\ \end{aligned} \]
5.1 MIS compensation
- BSDF 采样能够比较好的处理 glossy 材质,这些就不需要 guiding 部分来做了
- MIS compensation
- Karlík [2019]
- 在学习得到的 pdf 中减去一个常数,effectively enhances contrast
- TODO
- 论文策略:假设权重函数和 pdf 是独立的,如此,我们可以只学习如何采样
guided portion(而不需要学习整个积分项)
- MIS 权重和 pdf 独立的话,则两项之间也独立了
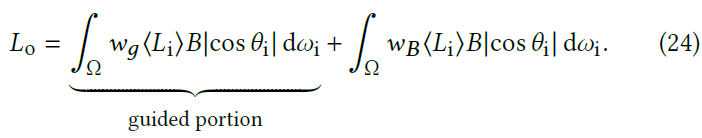
- 此时能够得到如下的结果
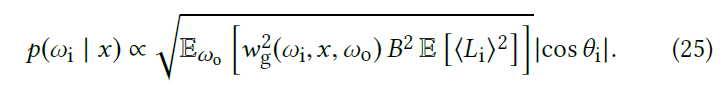
- 实际上,balance heuristic 和 pdf
并不是独立的,因此这是一个迭代学习的过程
- 迭代过程中:pdf 平滑变化 \(\to\) balance heuristic rate 平滑变化
5.2 Selection probability
- 使用 BSDF 有时已经就是最好的选择
- 例子:almost specular surfaces
- 此时,使用 MIS 可能也会带来较大的方差,需要较好的选择 \(\alpha\)
- 实际最优的 \(\alpha\) 是和 \(x,\omega_o\) 相关的
\[ \alpha(x,\omega_o) \]
- 但是在实际操作中,类似 path guiding
的算法都是学习到了一个区域内的最优值,这并不是 optimal 的
- \(\mathcal{D}\):some divergence function(e.g., Kullback-Leibler)
\[ \alpha(x\in S)=\mathop{\arg\min}_{\alpha}\;\mathbb{E}_{\omega_o}\left[{\mathcal{D}(p_{\text{eff}}\Vert p_{\text{zf}})}\right]\quad\quad(26) \]
- 其中
\[ \begin{array}{c} p_{\text{zf}}: \text{zero-variance}\\ p_{\text{eff}}=(1-\alpha)p_{\text{g}}+\alpha p_{B} \end{array} \]
- 这样的处理方式和式子12相比,只考虑了 \(\omega_o\)
- 场景:glossy ceiling,光源是中央的小片,朝上发光
- 不同的选择函数 \(\alpha\)

- guiding 策略的有效性依赖于 \(\omega_o\)
- 可以直接看见(天花板):BSDF 更优
- primary ray
- 直接看不见(墙壁):guiding 更优
- secondary ray(or more bounces)
- 可以直接看见(天花板):BSDF 更优
- 我觉得应该是 diffuse guiding 更优,glossy BSDF 更优
- 图中可以看出:
- 对于天花板,主要是直接光照亮的部分,PPG 倾向于还是使用 guiding,导致效果较差

- 我们的方案:根据贡献加权
- 直观上:对整个像素的贡献越高,权重越大,而不是只看局部的贡献
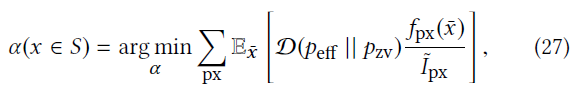
- 保证 guiding 不会带来太多问题,限制 \(\alpha\) 的最小值,例如:\(\alpha\ge0.1\)
- Finding more robust estimation schemes is a very important but orthogonal problem
6 APPLICATION I: PATH GUIDING
- PPG
- full
- 确定叶子节点的采样概率:
- \(D_k\):大小,这里用立体角衡量
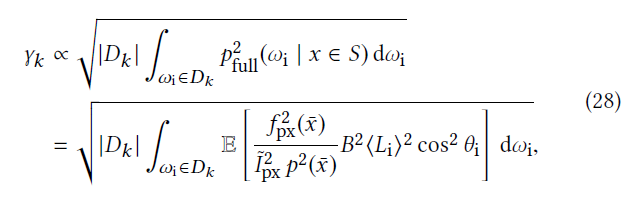
- PPG 回忆
- 每一轮训练都 reset,重新训练
- 修改如下图

- RelThroughput:在调用 RenderImage 的时候设置为 \(W_{\text{px}}/\tilde{I}_{\text{px}}\)
- sensor response / pixel estimate
7 APPLICATION II: LIGHT SELECTION
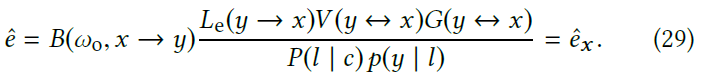
- \(y\) is a point on light source \(l\) in cluster \(c\)
- \(x\) is the shading point
- 具体的:TODO
- 效果:效果一般,没有显著提升
- 小光源 + glossy:效果不错
8 LIMITATIONS AND FUTURE WORK
- 独立的优化不一定得到最优的联合分布
- No strict proof that the isolated decisions will converge to an optimal joint distribution
- 训练不足时,效果较差
- 只限于单向 PT
其他
- 如果不应用 NEE,full 的训练时间会变长(超过 radiance 效果的训练时间)