(论文)[2021-CGF]Path Guiding Using Spatio-Directional Mixture Models

Posted on 2023-05-16 Edited on 2023-08-14 In CG.Paper Views:

通过 GMM 来近似 $L_i$ 项和 BSDF，然后使用它们的乘积去做 path guiding

SDMM

Path Guiding Using Spatio-Directional Mixture Models
CGF-2021
code

概述

SDMM：spatio-directional Gaussian mixture models
表示方法：GMM
- incident radiance ($L_i$) using a 5D Gaussian mixture model
- BSDFs ( fs) using $n$D Gaussian mixture models
好处
- 自然捕获 $L_i$ 中的 spatio-directional correlation（e.g. 视差 parallax）
- $n$D mixtures models 可以很好的表示参数化的 BSDF

挑战

坐标系
- product sampling：需要两个 GMM 在同一个坐标系中表示
  - shading frame：表面法向始终是 $(0,0,1)$
- 我们的 5D GMM 是在世界坐标中表示的（不能用 shading frame）
  - global coordinate frame
- 将 GMM 转化到 shading frame 中
  - 有形变（distortion），GMM 的中心位置
  - 尝试解决形变问题
    - tangent-space parameterization
    - first-order Taylor approximation
条件概率：$p(\mathrm{\omega}_i\vert \mathrm{x}_i)$
- 非线性、很难训练
- 只在每一次采样决策时，优化我们的 GMM
  - ？TODO
kD-tree 加速结构，用于训练 GMM

方法论

目标
- $\phi(x)$：BSDF 的参数表示

\[ p(\omega_i\vert\omega_o,x_i)\propto L_i(\omega_i,x_i)f_s(\omega_i,\omega_o,\phi(x))\cos(\gamma) \]

方法论

\[ p_{L_i}(\omega_i,x)\propto L_i(\omega_i,x) \]

\[ p_{f_s}(\omega_i,\omega_o,\phi)\propto f_s(\omega_i,\omega_o,\phi(x))\cos(\gamma) \]

实际采样

\[ p(\omega_i\vert\omega_o,x)\propto p_{L_i}(\omega_i\vert x)p_{f_s}(\omega_i\vert \omega_o,\phi(x)) \]

切线空间 GMM

spherical tangent-space Gaussian mixture models
- rotate the mixtures to the same coordinate frame
表示
- $\mu_k\in\mathbb{S}^2$：world-space unit-length mean vector
- $\sum_k\in\mathbb{R}^{2\times2}$：tangent-space covariance matrix

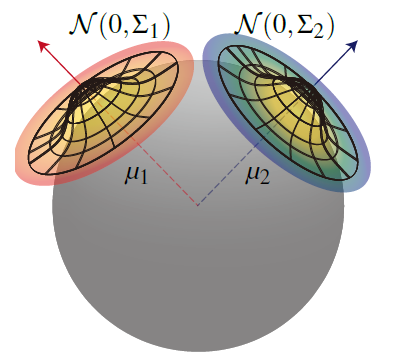
旋转只需要旋转 $\mu_k$ 即可
在 $\mu$ 处的切线空间（$\mu$-centered tangent space）
- $\omega\in\mathbb{S}^2$：world-space directions
- $v\in\{v\vert\Vert{v}\Vert<\pi\}$：tangent-space directions

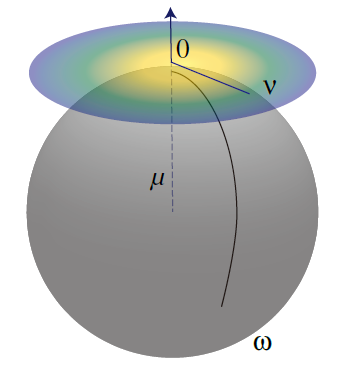
exp/log 变换

\[ v=\log_{\mu}(\omega),w=\exp_{\omega}(v) \]

azimuthal equidistant projection

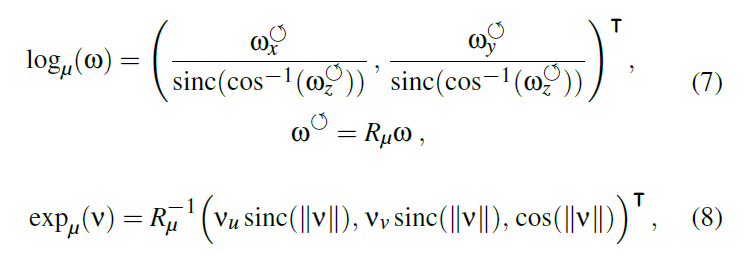
其中
- $R_{\mu}$：旋转矩阵，$\mu\to(0,0,1)$

\[ \text{sinc}(x)=\dfrac{\sin(\pi x)}{\pi x},unnormalized \]

该变换的优点：$\Vert{v}\Vert<\pi$
- 变换前后，从原点（$\mu$，$\mu$ 对应到 tangent space 中的点）到这个点的测地线距离不变

pdf

$\mu$-centered tangent space

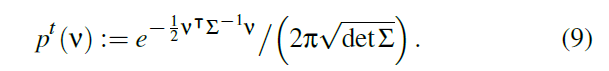
solid-angle：雅可比矩阵变换

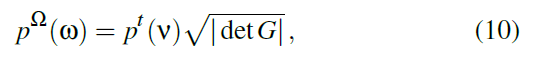
$G=J^{T}J$，$J\in\mathbb{R}^{3\times2}$
非方阵的行列式

\[ \vert{\det(J)}\vert=\sqrt{\vert{\det(J^{T}J)}{\vert}} \]

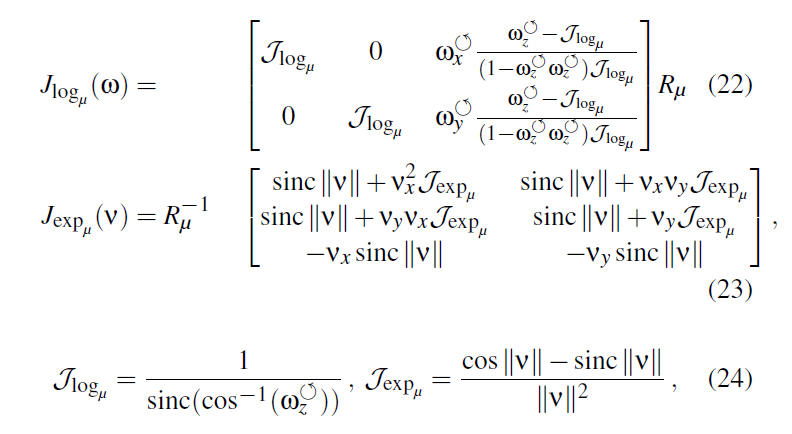
K个 tangent -space GMM
- 其中 $\pi_k$ 为权重系数，对每一个 $\omega$ 而言，和都为 1

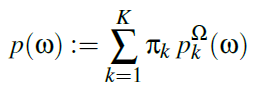
sampling

根据权重 $\pi_k$ 采样 $k$
根据第 $k$ 个 tangent-space GMM 采样 $v$
- 双射性质只在 $\Vert{v}\Vert<\pi$ 时满足，因此不满足时直接丢弃，使用 $p(\omega)$
  - 实际丢弃的很少（on average $0.021\%$）
计算 $\omega\leftarrow v$

Additional dimensions

额外的维度，例如 3D 位置 $x$，只需要平移即可
- 不需要旋转？
这样就从 spherical or Euclidean 坐标系转化到了 tangent-space

EM 学习

直接学习条件分布很复杂，我们选择学习联合分布，然后在过程中加上条件
EM 的思想：反复采样 GMM，更新主统计量，更新 GMM 参数（每次更新都让最大似然增大）

Mini-batch EM

初始样本：$x_1,\cdots,x_{M}\in\mathbb{R}^{D}$，以及他们的在蒙特卡洛框架中的权重 $w_1,\cdots,w_M\in\mathbb{R}$
计算主统计量

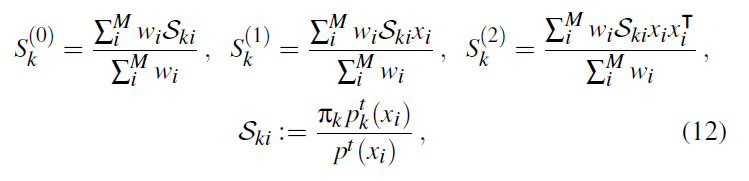
更新参数值

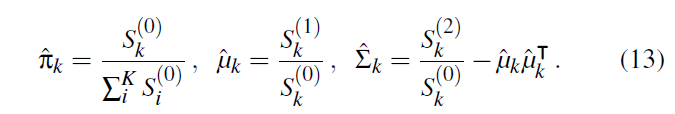
tangent spaces

给定初始的 $M$ 个样本，方向向量 $\omega_i\in \mathbb{S}^{2}$，权重 $w_i\in\mathbb{R}$
计算主统计量 $S_k^{(0)}$
计算 $\mu$-centered tangent-space $v_i$
计算主统计量 $S_k^{(1)}$
计算 $\hat{\mu}_k$

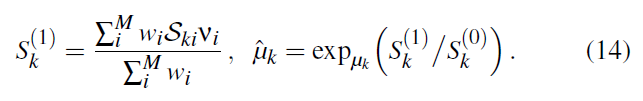
根据 $\hat{\mu}_k$ 计算 $S_k^{(2)}$（先算出 $\hat{v}_k$）
更新 $\hat{\sum}_k$
- 因为 $\hat{\sum}_k$ 和 $\hat{\mu}_k$ 绑定，而不是 $\mu_k$

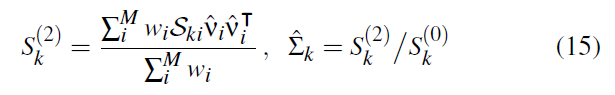
加上 3D 位置信息
- $\log$ 变换就是平移

Efficient Conditioning and EM

incident radiance field：
- 上千个 GM，都过一遍效率低
发现：只有 $\mu_k$ 接近 $x$ 的 GM 才会影响条件分布 $p_{L_i}(\omega_i,x)$
- $x$ 按照 AABB 最长轴归一化
- 可以用于加速
- EM 算法也能根据这一点加速
加速：spatial kD-tree partitioning
- 每个叶子节点保留 16 个 GM
- 同时也设置为 mini-batch 的训练数，这样不同的 GM 可以同时进行优化

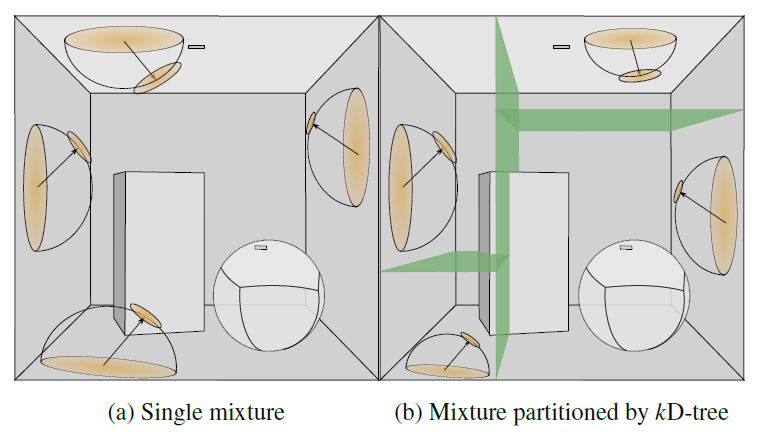
和不用 kd-tree 相比，结果差别不大，但是训练速度大幅度提升

product sampling

使用如下近似，代替更新（按照上面的方式需要根据 $\hat{\mu}_2$ 进行更新，这样很慢）
- $\mu_1$-centered，误差只在 $\mu_2$ 的 $\hat{\sum}_2$

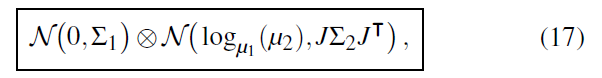
实际中：BSDF 作为 $\mu_2$

Implementation in a Renderer

BSDF 的训练是和 $L_i$ 的训练一起的，不需要预训练
- nD GM：n is the number of BSDF parameters
限制：isotropic BSDFs
- 各向异性需要增加 GM 的个数
均匀采样 $\phi,\omega_o$，根据 BSDF 重要性采样 $\omega_i$，mini-batch EM 用于优化
product sampling 的时候，只选择权重最大的两个 BSDF

Robust EM

$L_i$ 的优化：4spp 更新一次，总预算超过 $1/4$ 之后停止训练
EM 容易陷入局部极值，初始化尽量均匀
初始化
- 5D 均匀分布，空间 kd-tree（$8\times8\times8$）
- 初始化 GMM，至少 16 个样本（不够则等待）
  - kmeans++ 找出两个中心，然后每个中心构建均匀分布的 8 个 GM
训练轮
- 如果叶子节点的总样本数量大于 $c=16000$，则分裂（重新分布样本）
  - 递归进行
  - GMM 拷贝到子节点

？TODO