(论文)[2017-EGSR]Practical Path Guiding for Efficient Light-Transport Simulation

Posted on Edited on In Views:
通过空间二叉树、方向四叉树的混合结构去近似 $L_i$ 项，然后使用它去做 path guiding

PPG

概述

PPG

  • SD-Tree：空间二叉树 + 方向四叉树
    • 3D spatial domain of the light field
    • 2D directional domain
  • 每一个二叉树的叶子节点都包含一个四叉树

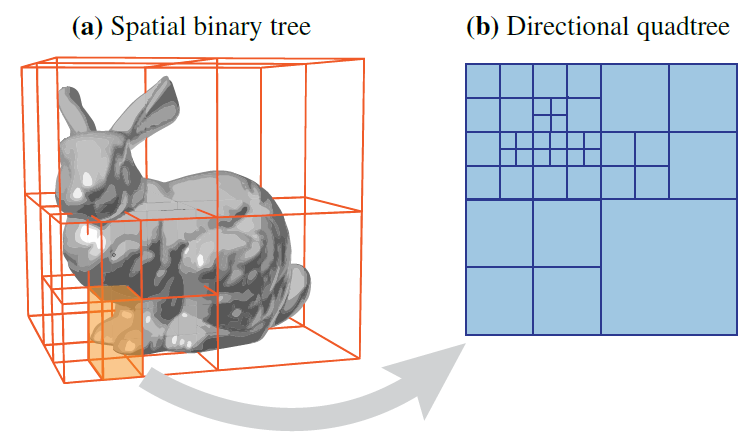
  • 优点：容易集成到 PT 框架里
  • 算法启发：path guiding 算法和复杂算法相比同样有效
  • 其他贡献：固定时间，找到最合适的训练时间/渲染时间分配

其他算法

  • 其他方法

    • constructing high-energy light paths
      • BDPT：Bi-directional path tracing
      • MLT：Metropolis light transport
    • offsetting the inefficiency by reusing computation
      • PM：Realistic Image Synthesis Using Photon Mapping
        • Instant radiosity
        • VCM：Light transport simulation with vertex connection and merging
        • A path space extension for robust light transport simulation
        • Gradient-domain path tracing

  • 其他存储方式

    • spatially cached histograms：Importance driven path tracing using the photon map
    • cones：Importance sampling with hemispherical particle footprints
    • gaussian mixtures model（GMM）：On-line learning of parametric mixture models for light transport simulation

介绍

  • guiding 的概念
    • Importance driven path tracing using the photon map（histograms）
    • A 5d tree to reduce the variance of monte carlo ray tracing（5D tree）
  • path guding 的改进
    • Global Importance Sampling of Glossy Surfaces Using the Photon Map（discretized BSDF、caustics）
    • Importance sampling with hemispherical particle footprints（cones、irregular）
    • On-line learning of parametric mixture models for light transport simulation（gaussian mixtures）
    • Product Importance Sampling for Light Transport Path Guiding（和 BSDF 一起重要性采样）
    • Adjoint-driven russian roulette and splitting in light transport simulation
    • Learning light transport the reinforced way（结合训练+渲染）
  • PPG
    • adjoint-based Russian roulette
    • progressive reinforcement learning
    • fusing the rendering and learning algorithms into one
    • 每一个 pass 都是 unbiased
  • 混合存储表示
    • Volume-Surface Trees
    • Rasterized bounding volume hierarchies
    • spatial octree and a directional kd-tree：Spatial directional radiance caching

算法

  • two SD-trees
    • one for guiding the construction of light paths
    • another for collecting MC estimates of incident radiance
  • double the number of samples across iterations
  • 近似渲染方程中的 \(L(x,\omega)\) 项
    • incident radiance field

\[ L_{o}(x, \omega_{o})=L_{e}(x, \omega_{o})+\int_{\Omega} L_{i}(x, \omega_{i}) f_{r}(x, \omega_{i}, \omega_{o})(n \cdot \omega_{i}) d \omega_{i} \]

收集 L

  • 对得到的光路的每一个顶点做收集
    • 顶点 \(v\)：\[L(x_v,\omega_v)\]
  • binary tree
    • 找到包含 \(x_v\) 的叶子节点，记录 \(L\)
  • quadtree
    • 继续向下搜索，进入包含 \(\omega_v\) 的叶子节点，在这些节点上都记录 \(L\)
    • pdf over all leaf node in quadtree

空间二叉树

  • 选择
    • 交替使用 \(x,y,z\) 轴
    • always split the node in the middle
  • 细化
    • 如果一个叶子节点的计数（\(L\) 记录次数）大于等于 \(c\cdot\sqrt{2^k}\)，则分裂
      • \(k\)：迭代轮次
      • \(2^{k}\) 正比于发射的光线数目
      • \(c\)：二叉树的分辨率、四叉树的收敛率相关
    • 分裂的时候，计数平均分给两个子节点
  • 每一个的叶子节点的计数 \(\approx c\cdot\sqrt{2^k}\)
  • 叶子节点的数量正比于 \(\dfrac{2^k}{c\cdot\sqrt{2^k}}=\dfrac{\sqrt{2^k}}{c}\)（一条光线，\(d\) 个记录，\(d\) 稳定）
  • \(c\) 的确定
    • \(s\)：quadtree 每一个树节点的期望样本数
      • 根据 quadtree 的拆分规则，每一个叶子节点采样概率基本接近（flux 接近）
      • 单个 quadtree：\(s=\dfrac{S}{N_l}=\dfrac{总样本数}{叶子节点数}\)
    • 根据 \(S\approx c\cdot\sqrt{2^k}\)，可以得到
      • 实验测试，\(N_l\approx300\)
      • \(s=40\) 收敛效果就已经不错了
      • 初始设置 \(c\)（\(k=0\)）

\[ c\approx\dfrac{S}{\sqrt{2^k}}=\dfrac{s\cdot N_l}{\sqrt{2^k}}=12000 \]

方向四叉树

  • 每轮迭代结束之后都重建，更好地反映 flux 分布
  • 目的：根据上一轮收集的 flux, 每个节点的收集的 flux 都不超过 \(\rho=1\%\)
    • 当前节点/根节点
  • 初始化
    • 存在：上一轮的迭代结果
    • 新生成：父节点的 quadtree
  • 从根节点开始，对于叶子节点，如果超过 \(1\%\)，则展开这个节点，把这个节点的 flux 均分给子节点
    • 递归进行
    • 内点则可以剪枝（\(<1\%\) 则子节点必然 \(<1\%\)）
  • 结果：Spherical regions with high incident flux are thus represented with higher resolution

训练与渲染

  • 序列：\(\hat{L}^{1},\hat{L}^{2},\cdots,\hat{L}^{M}\)
    • \(\hat{L}^{1}\)：BSDF sampling
    • \(L^{k}(k>1)\)：BSDF + \(\hat{L}^{k-1}\)（MIS）
  • 采样过程：路径节点 \(v\)
    • 找到包含 \(x_v\) 的叶子节点，获得 quadtree
    • 采样策略：Probability trees
      • 按照记录的 flux 进行采样

样本数

  • 每轮迭代 \(\times2\)
  • 平衡训练与渲染
    • 每轮都相同，为 \(s\)
      • 则每次只有 \(s\) 个样本用于图像生成，\(ks\) 的都是用于训练
    • \(\times2\)
      • 则每次有 \(2^k\) 个样本用于图像生成，\(2^{k+1}-2\)
  • 让到达叶子节点的采样数类似
    • 分裂叶子节点数 \(\times2\)
    • 样本数 \(\times2\)

渲染

  • 只使用当前迭代轮的样本
    • unbiased：样本之间是独立的
  • 最终视频展示：当 \(k\) 轮的 path 样本数高于 \(k-1\) 轮时，替换展示图

平衡训练与渲染

compute budget

  • 总预算（budget）：\(B\)
    • \(B\) 的选择：样本数、时间
  • define the budget to unit variance：\(\tau_k=V_k\cdot B_k\)
    • \(I_k\)：第 \(k\) 轮迭代生成的图片
    • \(V_k\)：\(I_k\) 的 mean variance of pixels
    • \(B_k\)：构建 path 的开销
  • \(\hat{B}_k\)：剩余预算

\[ \hat{B}_k=B-\sum_{i=1}^{k-1}B_k \]

  • 最终图的方差估计

\[ \hat{V}_k=\dfrac{\tau_k}{\hat{B}_k} \]

  • 目标：找到最小的 \(\hat{k}\)，使得最小化最终的方差

\[ \hat{k}=\mathop{\arg\min}_{k}\hat{V}_k \]

  • 假设：\(\tau_k\) 单调递减 + 凸函数
    • 此时能够推出 \(\hat{V}_k\) 也是凸函数（证明有问题，见附录）
    • 于是只需要找到最小的 \(k\) 满足 \(\hat{V}_{k+1}>\hat{V}_k\) 即可（多计算一次，但是是值得的）
  • 如果缺少了凸函数的保证，则找到的结果只是一个局部最优

target variance

  • 类似方法
  • 渲染预算：\(\bar{B}_k\)
  • 目标方差：\(\bar{V}\)
  • \(\bar{B}_k\) 的估计 \(\dfrac{\tau_k}{\bar{V}}\)
  • 总预算

\[ \tilde{B}_k=\bar{B}_{k}+\sum_{i=1}^{k-1}B_i \]

  • 找到 \(\hat{k}\)

\[ \hat{k}=\mathop{\arg\min}_{k}\tilde{B}_k \]

  • \(B_k\) 单调递增，且是凸函数（样本加倍）
    • 只需要找到 \(\tilde{B}_k>\tilde{B}_{k-1}\) ，训练停止
    • 直观理解，花了更多时间，但是不能够获得期望的方差减小收益

\[ \begin{aligned} \tilde{B}_k&=\bar{B}_{k}+(\tilde{B}_{k-1}-\bar{B}_{k-1})+B_{k-1}\\ &=\tilde{B}_{k-1}+(\bar{B}_{k}-\bar{B}_{k-1})+B_{k-1} \end{aligned} \]

实验结果

  • equal time
    • GMM/SD-Tree 都是不使用 NEE 的（加强对比）
    • GMM 的预训练时间不算入（说明我们更好）
  • 不加 importance sampling（正交的，都可以加）

场景

  • TORUS
    • very long chains of specular interactions
    • a significant amount of specular-diffuse-specular (SDS) light transport
  • POOL
    • difficult SDS light transport
  • KITCHEN
    • various glossy materials
    • complex geometries

分析

Convergence

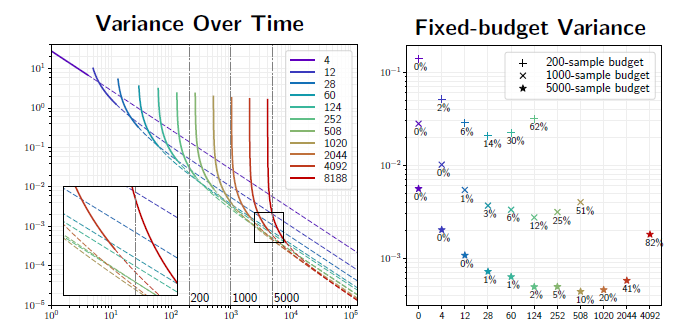
  • 左图：不同的线表示使用不同的样本数进行训练
    • 每轮迭代使用的样本数加倍
      • 每轮增加：4、8、16、32、……
      • 每轮总共：4、12、28、60、……
    • 延长线：收敛率，使用当前分布继续渲染
  • 右图：固定样本数，在左图中作 \(x=\text{samples}\)，得到的交点
    • 不同的点类型表示总预算（总样本数）不同

Memory Usage

  • 根据展开原则，叶子节点数不小于 \(\dfrac{1}{\rho}\)
  • 上限无界
    • 实现中设定最大深度为 20
  • quadtree 节点数上限：\(20\cdot\dfrac{4}{\rho}\)
    • 最差情况下，叶子节点都是刚分裂形成的，流量 \(\ge \dfrac{\rho}{4}\)
    • 因此叶子节点数 \(\le\dfrac{4}{\rho}\)
    • 每一层的节点数肯定都小于总的叶子节点数：\(\le20\cdot\dfrac{4}{\rho}\)
  • 实际测试
    • \(\rho=0.01\Rightarrow \text{max-node}=8000\)
    • 平均：300
    • 最大：792
  • SD-Tree 的存储：只需要保存最新的两棵树 \(\hat{L}^{k},\hat{L}^{k-1}\)
    • spatial 只需要保存一棵树，每个叶子节点包含两个 quadtree
    • 相当于只是更新了
  • 测试：整个分布 \(<20\text{mb}\)

讨论

  • directional quadtree distributions
    • 当前：world-space-aligned cylindrical coordinates
      • 其他：hemispherical
    • 优点：不需要判别、很容易扩展到 volume path tracing
  • quadtree
    • 其他：Gaussian Mixture Model
      • 随着空间位置变化大
      • 不一定能找到全局最优
    • 优点：increased robustness
  • temporal path guiding
    • 容易扩展，增加一个维度 \(t\) 就行
  • 采样策略
    • MIS with BSDF sampling
    • 改进
      • ignore quads in the bottom hemisphere
        • Portal-masked environment map sampling
      • Importance resampling
    • 直接对乘积采样
      • BSDF and the incident radiance
        • Product Importance Sampling for Light Transport Path Guiding
    • Importance sampling spherical harmonics
      • incident radiance distributions 转化为 Haar wavelets
      • BSDF 使用 spherical harmonics 表示
  • 开 NEE
  • 集成到复杂框架中：对 BDPT、VCM 也有好处
    • On-line learning of parametric mixture models for light transport simulation

附录

凸函数证明

  • \(\hat{V}_k\) 凸函数性质证明
  • 只要证明

\[ 2\hat{V}_k\le\hat{V}_{k+1}+\hat{V}_{k-1} \]

  • 等价

\[ \begin{aligned} &\dfrac{2\tau_k}{\hat{B}_k}\le\dfrac{\tau_{k+1}}{\hat{B}_{k+1}}+\dfrac{\tau_{k-1}}{\hat{B}_{k-1}}\\ \Leftrightarrow\quad& 2\tau_k\le\dfrac{\hat{B}_k}{\hat{B}_{k+1}}\tau_{k+1}+\dfrac{\hat{B}_{k}}{\hat{B}_{k-1}}\tau_{k-1}\\ \end{aligned} \]

  • 如果下式成立，则上式成立
    • 凸函数：\(2\tau_k-\tau_{k-1}\le\tau_{k+1}\)

\[ \begin{aligned} &2\tau_k\le\dfrac{\hat{B}_k}{\hat{B}_{k+1}}(2\tau_k-\tau_{k-1})+\dfrac{\hat{B}_{k}}{\hat{B}_{k-1}}\tau_{k-1}\\ \Leftrightarrow\quad& 2\tau_k\le2\tau_k\dfrac{\hat{B}_k}{\hat{B}_{k+1}}+\left(\dfrac{\hat{B}_{k}}{\hat{B}_{k-1}}-\dfrac{\hat{B}_{k}}{\hat{B}_{k+1}}\right)\tau_{k-1}\\ \end{aligned} \]

  • 因为有 \(\tau_k<\tau_{k-1}\)，则下式成立即上式成立

\[ 2\tau_k\le2\tau_k\dfrac{\hat{B}_k}{\hat{B}_{k+1}}+\left(\dfrac{\hat{B}_{k}}{\hat{B}_{k-1}}-\dfrac{\hat{B}_{k}}{\hat{B}_{k+1}}\right)\tau_{k}\\ \]

\[ 2\le\dfrac{\hat{B}_{k}}{\hat{B}_{k-1}}+\dfrac{\hat{B}_{k}}{\hat{B}_{k+1}}\\ \]

  • 转化为只含有 \(\hat{B}_k\) 之后，利用 \(B_k\) 单调递增性质（样本加倍）

\[ 2\le\dfrac{\hat{B}_{k}}{\hat{B}_{k}+B_{k-1}}+\dfrac{\hat{B}_{k}}{\hat{B}_{k}-B_k}\\ \]

  • 等价于

\[ B_{k-1}-B_{k}-\dfrac{2B_{k-1}B_{k}}{\hat{B}_k} \]

ERROR

  • \(\hat{B}_k\) 递减

\[ \hat{B}_k=\hat{B}_{k-1}-B_{k-1}<\hat{B}_{k-1} \]

\[ \dfrac{\hat{B}_{k}}{\hat{B}_{k-1}}-\dfrac{\hat{B}_{k}}{\hat{B}_{k+1}}<0 \]

  • 于是 \(\tau_k<\tau_{k-1}\) 这一步转换有问题

观点

  • 其他有趣论文
    • Gradient-domain path tracing
    • On-line learning of parametric mixture models for light transport simulation
      • gaussian mixtures
    • Importance resampling for global illumination
    • Portal-masked environment map sampling

TODO

  • TODO
  • we use world-space cylindrical coordinates to preserve area ratios when transforming between the primary and directional domain
  • 论文：Probability trees