(论文)[2002] Exact From-Region Visibility Culling

Posted on Edited on In Views:
论文阅读

Exact From-Region Visibility Culling

  • S. Nirenstein, E. Blake and J. Gain
  • Department of Computer Science, University of Cape Town, Cape-Town, Rondebosch 7701, South Africa

思路

  • 对于两个多边形之间的可见性判断，我们将能够同时穿过这两个多边形的直线集合映射到普吕克空间中的一个点集 \(A\) ，同时我们对每一个 occluder，将通过他的直线也映射到普吕克空间中的一个点集，在 \(A\) 中减去这个点集，直至 \(A\) 为空（不可见）或者处理完所有的 occluder（可见）

摘要

  • 可以处理百万计的多边形
  • 关键思想
    • The essence of our idea is to represent 3-D polygons and the stabbing lines connecting them in a 5-D Euclidean space derived from Plücker space and then to perform geometric subtractions of occluded lines from the set of potential stabbing lines.
    • 将 3 维的多边形和连接他们之间的 stabbing lines 用 5 维的欧几里得空间（派生自普吕克空间）表示，然后在潜在的 stabbing lines 的集合中做遮挡线的减法
  • 建立了 query architecture

1. Introduction

  • 一般有两种方式
    • run-time：一般是单点对于场景的可见性
    • pre-process：建立任何点（小区域）的可见几何体集合

From-Region visibility

  • 将视点空间（VPS：view-point space）划分为有限个区域（region/cell）
    • 而不是处理无限的可能的相机位置
  • 好处
    • 能够将运行时的计算开销转移到预处理中
  • 问题
    • 由于是预处理，只能够处理一些静态的场景

From-point visibility

  • 计算成本相对较低，可以在逐帧渲染的时计算（run-time）
    • 因此适合在动态场景中使用

一个分类

image-20211005164143617

  • conservative：保守的
    • 高估可见性，从而带来 false visibility 的问题
    • 会将一些不可见的多边形带到渲染那一步
  • aggressive：激进的
    • 低估可见性，带来 false invisibility 的问题
    • 会导致最终结果图片错误
    • 只有在如下情况才可用
      • 误差部分相对较小，可以接受
      • 算法特别快
      • 场景在使用保守方法的情况下先很难有效求解
  • approximate：估计的
    • 会出现 false visibility、false invisibility 的问题，一般只用于需要快速出结果的时候
  • exact：精确的
    • 结果产生的图片是准确的，渲染的时候没有一个多边形是多余的
    • 本质上也是保守的，因为把一个区域看成了一个整体（实际物体可能较小）

精确渲染的优势

  • 不是场景依赖的，对所有的场景都能够用一样的方式解决
    • 其他方式可能是场景依赖的
  • 可以提供一个 benchmark，用于评估其他的可见性提出算法
    • 一个更准确的度量，可以有以下指标，而不是之前的知识粗糙的计算被剔除三角形的百分比
      • type(false visibility or false invisibility),
      • distribution(clustered or widespread)
      • exact magnitude
      • visibility error

本文

  • 第一次提出了一个针对现实场景的、精确的可见性剔除算法
    • 1.5M 个三角形
  • 相较之前的方法有 3 个数量级的改进
  • 虽然可以处理大型的场景，但是预处理成本很高

本文的贡献

  • Localised Exact Visibility
    • 能够精确计算两个凸多边形之间的可见性
  • Query Driven Architecture
    • 会保存之前计算的结果，用于之后的计算

2. previous work

  • From-Point Visibility 方面的 survey
    • D. Cohen-Or, Y. Chrysanthou, C. T. Silva, and F. Durand. A survey of visibility for walkthrough applications. Course 30, SIGGRAPH, August 2001.
    • F. Durand. 3D Visibility, analysis and applications. PhD thesis, U. Joseph Fourier, 1999. http://graphics.lcs.mit.edu/fredo.
    • H. Zhang. Effective Occlusion Culling for the Interactive Display of Arbitrary Models. PhD thesis, University of North Carolina at Chapel Hill, 1998

保守策略（准确的图片）

  • Cell-portal rendering
    • 试图建立所有 cell 之间的相对可见性，可见即在两个 cell 之间存在一条光线
    • Teller 提出了一个解析的方法解决这个问题，同时他将其扩展了，使其能够判断可见的 cell 的哪一部分才是可见的
    • 对建筑场景很有效，但不是通用的解决方案
    • 对组合复杂度比较低的场景有效
  • Cohen-Or、Saona-Vásquez 等提出了一个更加通用但是保守的方案
    • 对于一个物体和一个 view-cell，当且仅当被一个多边形挡住（所有 view-cell 中的点都看不见这个物体），这个物体才被认为是不可见的
    • 过于保守了，因此只有在 view-cell 相对场景中的多边形很小的情况下才能得到比较好的效果
    • 精细场景则需要大量的 view-cell，因此效率很低
  • 因此有必要将小的 occluder 进行聚合
  • Durand 提出一种通用方法，采用扩展投影算子（extended projection operator）的方法
  • Law、Tan 提出遮挡简化（occlusion preserving simplification）的方式生成更粗糙的细节、更大的多边形 occluder，同时保持了保守性
    • 不考虑有这个粗糙表示产生的遮挡
    • 没太明白
  • Koltun 等人利用分隔线构建更大更有效的虚拟遮挡器来代表许多较小的遮挡器
    • 不需要保存每一个 view-cell 的可见集合
  • Wonka 提出了一个保守的 2.5D 的方案，收缩 occluders，通过采样的方法求解可见性
    • 采样数足够多则趋向于精确解

激进策略

  • 基于 from-point 的策略，会产生 false invisibility 的错误，这些策略基于的想法是将那些对最终图像贡献很小的物体在渲染之前去除
  • Andújar 使用几乎不可见集合（hardly visible sets），去除那些只有部分可见的物体集合
  • Klosowski and Silva 提出优先层投影算法（prioritised layer projection algorithm），启发式的先绘制可见的物体，因此即使算法过早停止也能够保证渲染出来的结果还不错
  • Gotsman 提出基于采样的可见性算法
    • 使用 5 个维度（3D 空间 + 2D 角度），每一个 5D 的 cell 对应三维空间中的一个 beam
      • 2D 角度是为了加速剔除
    • 投射足够多的光线，在某个统计模型下，推断出物体可见、不可见、还是需要继续投射光线
    • trade-off：预处理需要花费的时间，准确率

精确策略

  • 一般是以某种结构构建双线空间（dual line space），直接暴露出可见性事件（visibility event）
    • A visibility event occurs when a topological change in visibility occurs in the scene.
  • 一些结构
    • aspect graph
    • 3D visibility complex
    • the visibility map
  • Teller：Plücker parameterisation of line space.
    • 算法有效性受到场景复杂度的限制
  • Durand：直接计算可见性实体的低维元素（骨架），构建出可见性事件的表面
    • 这样，由于简化导致的误差都是局部的，鲁棒性更强
  • Koltun：使用 dual ray-space 重新表示了两个部分之间的光线
    • occlusion：遮挡光线的空间是否包含了所有在 view-cell 和物体之间的光线

2.1 Plücker Line Space

  • 普吕克线性空间
  • 普吕克空间是格拉斯曼坐标系统（Grassmann coordinate system）的特殊情况
    • Grassmann coordinates allow for the parameterisation of a k-dimensional affine sub-space embedded in an n-dimensional space as a point in a projective \({k+1\choose n+1}-1\) dimensional space.
    • 什么玩意儿？

普吕克空间

  • 其他补充可以查看文章
  • lines（k=1），\(\mathbb{R}^3\)（n=3），投影的 5 维空间 \(\mathbb{P}^5\)
  • 三维空间中的有向直线 \(l\)，经过两点 \(P(p_x,p_y,p_z),Q(q_x,q_y,q_z)\)
  • 映射到普朗克空间中得到 \(\Pi(l)=(\pi_1,\pi_2,\pi_3,\pi_4,\pi_5,\pi_6)\)

\[ \begin{aligned} \pi_1&=q_x-p_x\\ \pi_2&=q_y-p_y\\ \pi_3&=q_z-p_z\\ \pi_4&=q_zp_y-q_yp_z\\ \pi_5&=q_xp_z-q_zp_x\\ \pi_6&=q_yp_x-q_xp_y\\ \end{aligned} \]

几何理解
  • 我们定义 \(d=p-q,m=p\times q\)，通过 \(d\) 和 \(m\) 能够唯一确定一条有向直线
    • \(d\) 确定直线方向
    • \(m\) 确定直线位置
  • 6 个维度对应普吕克坐标
代数理解
  • P, Q 的齐次坐标表示为 \(P(p_x,p_y,p_z,1),Q(q_x,q_y,q_z,1)\)
  • 定义普吕克坐标为 \(\pi_{ij}=p_iq_j-p_jq_i\)
    • \(\pi_{ii}=0,\pi_{ij}=-\pi_{ji}\)
  • 因此只有 6 个独立变量，对应普吕克坐标
二元映射
  • 定义二元映射：\(D_{\pi}(x)\)，其中 \(\pi,x\in\mathbb{P}^{5}\)

\[ D_{\pi}(x)=\pi_{0}x_{3}+\pi_{1}x_{4}+\pi_{2}x_{5}+\pi_{3}x_{0}+\pi_{4}x_{1}+\pi_{5}x_{2} \]

  • \(D_{\pi}(x)=0\) 的解被称为是 \(\pi\) 在 \(\mathbb{P}^5\) 中的双超平面
  • 给定直线 \(l_1,l_2\)，我们称他们是关联的（incident），当且仅当 \(D_{\pi_1}(\pi_2)=0\)（同时成立 \(D_{\pi_2}(\pi_1)=0\)）
  • 直线的位置关系

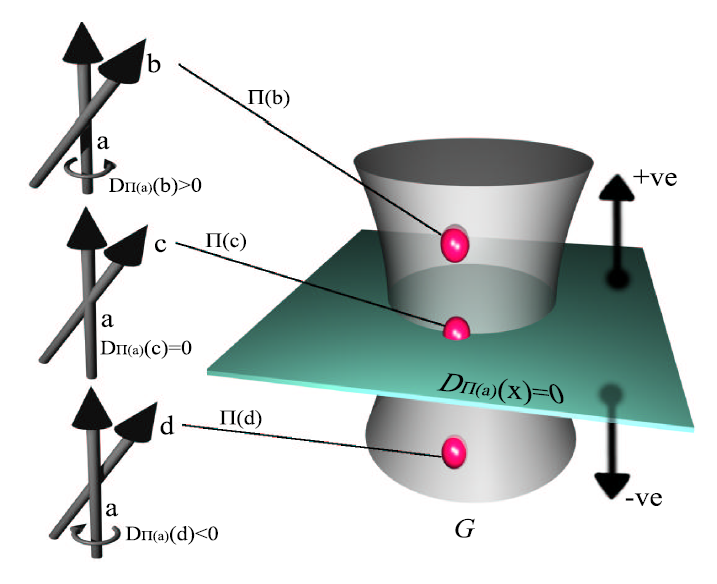
  • 并不是所有的 \(\mathbb{P}^5\) 中的点都能够映射到 \(\mathbb{R}^3\) 中
  • \(\Pi\) 是 \(\mathbb{R}^3\) 到 \(\mathbb{P}^5\) 子集的一个双射，这个子集被称为表示如下

\[ G=\left\{D_{x}(x)=0,x\in\mathbb{P}^5\right\}\backslash \{\textbf{0}\} \]

  • 这个子集的名称有多个
    • Grassmann manifold
    • the Klein quadric
    • the Plücker hypersurface

3. visibility query

3.1 overview

  • 为了精确查询，我们需要对同时刺穿两个多边形的线建立起一个空间表示
  • 实际处理的时候，我们简单地将所有多边形几何裁剪到由多边形对的顶点定义的凸包的内部，再处理这内部的线段即可
  • 每一个 occluder 都会遮挡住一部分两个 query polygon 之间的线，如果所有的线都被挡住了，那么 query polygon 之间相互不可见
  • 两个多边形之间的线被表示成普吕克超曲面 \(G\) 上点的一个连通子集，同样每一个 occluder 挡住的线也被表示成 \(G\) 上的一个点的连通子集
  • 算法思想
    • 首先将 un-obstructed volume 初始化为两个多边形之间的所有直线构成的点集
    • 针对所有的 occluder，我们在 un-obstructed volume 中去除它遮挡的那部分点集
      • 使用 5 维结构立体几何实现去除
      • CSG(constructive solid geometry) in five dimensions
    • 最终剩余的点集对应的直线就是未被挡住的直线
      • 如果集合为空，则两个多边形之间互相不可见
      • 如果非空，则互相可见，而且由他们之间可见直线的完整描述

3.2. 多边形之间的线空间

  • 直接对普吕克超曲面进行操作比较困难，因为是曲面
  • 我们构造了一个多面体，这个多面体和普吕克超曲面的交集便是结果

多面体构造过程

  • 如果一条直线 \(s\) 穿过了两个多边形，充要条件如下
    • s 和多边形的所有边的位置关系相同（左右手螺旋关系）

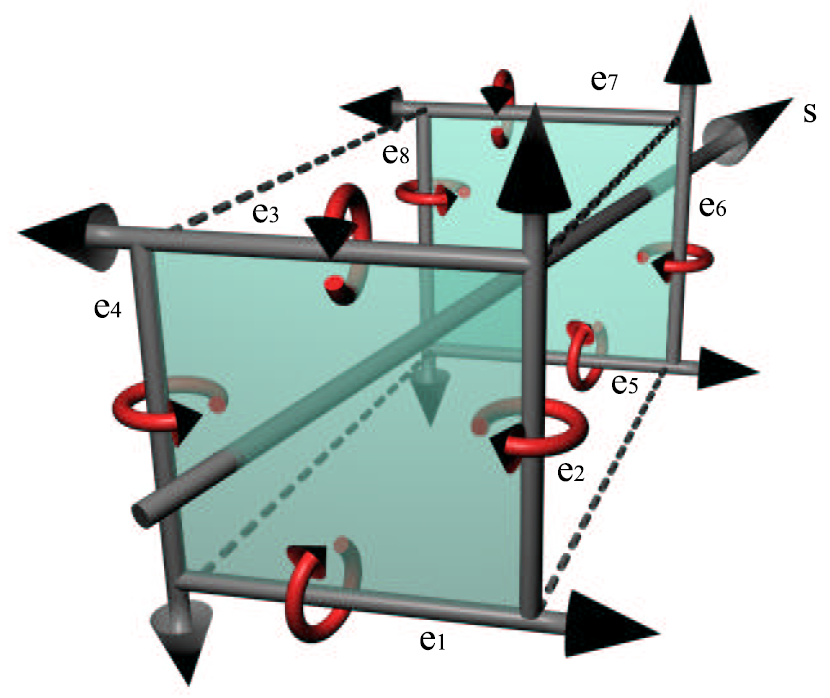
  • 给定两个多边形的边集 \(e_1,\cdots,e_n\)（appropriately directed）,判断一个直线是否和两个多边形相交，就是判断如下式子是否成立
    • 如何保证两个多边形边的方向一致？

\[ D_{\pi}(\Pi(s))\ge0,\forall\pi\in\left\{\Pi(e_1),\cdots\Pi(e_n)\right\} \]

  • 因为我们知道普吕克超平面上的点乘以一个常数因子之后，在三维空间终对应的点是不变的，因此我们可以将其除以某一项之后，将其归一化
    • 这一项不能为 0
    • 可以通过预旋转场景来实现
    • 正负问题？
  • 我们将第三项用于归一化（\(x_3=1\)）
    • \(\pi\) 不一起归一化：正负号的问题，如果 \(\pi\) 归一化，会出现正负号的问题
    • \(-\Pi(e)\) 和 \(\Pi(e)\) 表示的是两条边，方向相反

\[ D_{\pi}'(x)=\pi_{0}+\pi_{1}x_{4}+\pi_{2}x_{5}+\pi_{3}x_{0}+\pi_{4}x_{1}+\pi_{5}x_{2} \]

  • \(G\) 平面现在如何在 \(\mathbb{R}^5\) 中表示？
    • 如果是等于零的话，似乎都归一化也没啥关系，怎么和上面的表达式统一呢？
  • 于是我们现在使用一个定义在 \(\mathbb{R}^5\) 中的几何体来表示 \(\mathbb{R}^3\) 中的直线集合

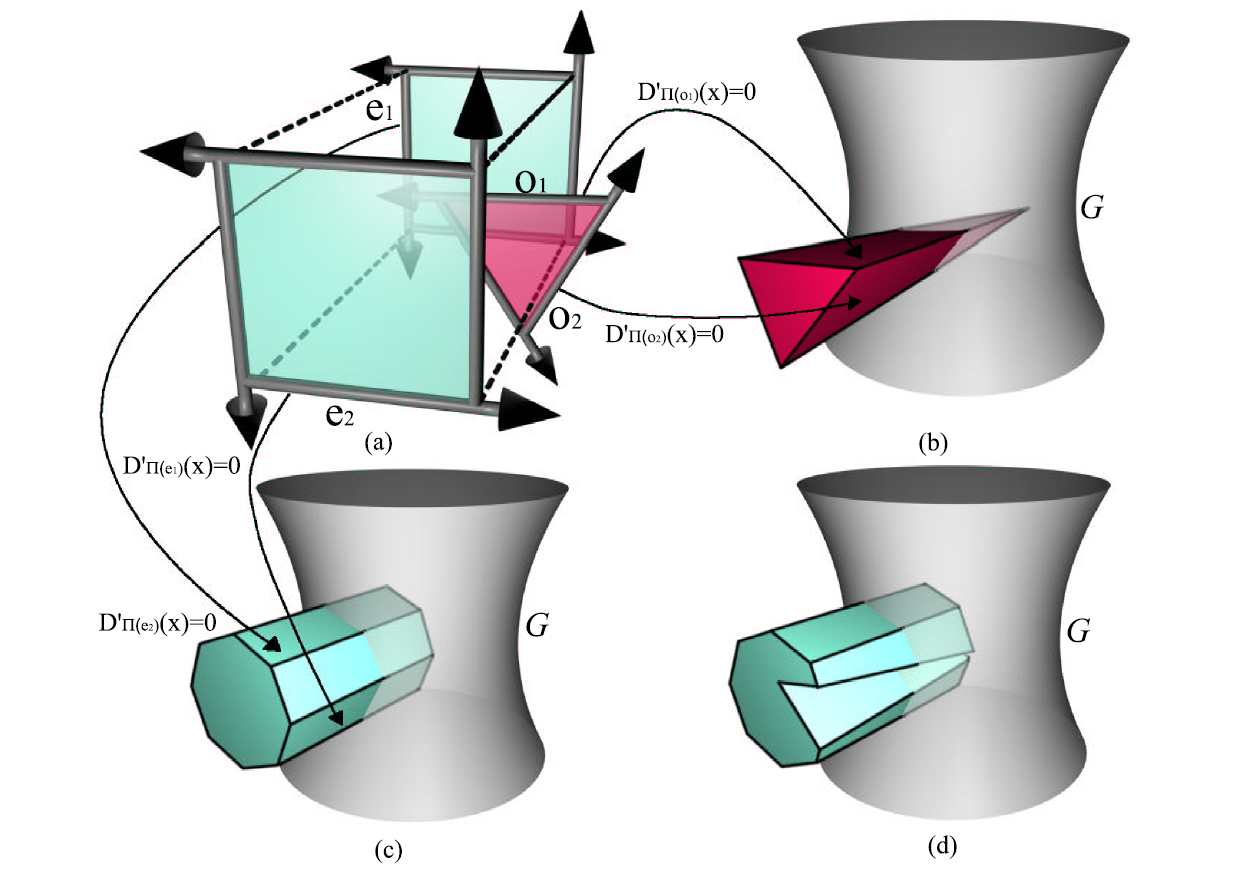
  • 上面这样的多面体可能是无界的，但是多面体和普吕克超曲面的交点集是有界的，因此我们可以在不改变多面体和普吕克交点集的前提下对多面体增加限制，使其有界

3.3 普吕克空间中的 CSG

  • CSG：构造实体几何，全称 Constructive solid geometry ，是 3D 计算机图形学中构建模型的常用技术，可通过合并 Union、相减 Subtraction 和相交 Intersction 的三种取集的逻辑运算，将立方体、圆柱体和棱柱等简单的基础模型，嵌套组合成更复杂三维模型
  • 针对一个 occluder
    • 我们将它的所有边使用 \(\Pi,D'\) 表示成 \(\mathbb{R}^5\) 中的超平面
      • \(D'_{\Pi(o_1)}(x),x\in{\mathbb{R}^5}\) 表示和 \(o_1\) 共面的所有直线
    • 这个超平面围成的区域就是穿过这个 occluder 的所有直线
    • 我们维护一个有向超平面的集合 \(\mathcal{O}\) 来表示上面的区域
  • 在五维空间中，如何在一个多面体中减去另外一个多面体是一个比较困难的任务（non-trivial）
    • 我们给出一个算法，将所有的多面体进行一个拆分（拆分成若干部分），使得每一个部分对于任意一个超平面来说，都恰好落在他的一侧
      • 这是可以实现的，因为对于一个多面体和一个超平面而言是 OK 的
    • 如果包围某一个部分的超平面集合中的元素全在 \(\mathcal{O}\) 中，那么这个部分就是完全被遮挡的，我们可以移除这个部分
    • 剩下的部分和普吕克超平面的交集就是没有被这个 occluder 挡住的直线集合了
  • 上面这个操作是迭代进行的
    • 初始化一个区域，这个区域对应 query polygons 的有向超平面围成的部分，\(\mathcal{O}\) 初始化为空集
    • 对于每一个 occluder，将新的边加入 \(\mathcal{O}\)，将上面的部分进行切分使得满足每一个部分都恰好在 \(\mathcal{O}\) 中任意一个超平面的一侧，去除其中完全被 \(\mathcal{O}\) 中的有向平面挡住的部分
    • 直至这个区域为空（完全被遮挡），或者所有 occluder 都检测完这个区域还不为空（互相可见）
  • 如何切割一个部分？
    • 遍历这个部分的 5 个维度，切割成为两个部分
    • 有冗余，因为被拆分的面被重复记录了，但是这样更快
  • 如何判断超平面和一个部分相交？
    • 首先使用一个 5D 的包围球去进行测试，如果不相交则不相交
    • 如果相交则使用精确的顶点表示的超平面去测试
      • 判断是否存在两个点位于超平面的两边，是则相交，否则则不相交

3.3 优化策略

  • 当我们考虑 occluder 的超平面集 \(\mathcal{O}\) 对整个实体进行切割的时候，我们只考虑切割穿过切割那些穿过 \(\mathcal{O}\) 边界的部分
    • 如果切割新形成的部分 \(\mathcal{O}\) 和普吕克超平面没有交集，那么我们直接丢掉着一个部分
  • 在算法开始之前，我们先尝试从一个多边形投射出若干条光线，如果存在一条光线能够打到另外一个多边形，那么就说明是可见的，只有不存在这样的光线的时候，我们才使用上面提到的算法
  • 通过分析之前投射的光线，分析出使用最少的多边形就形成完全遮挡的效果，从而尽早终止算法
    • 挡住光线最多的 occluder 先从原来的结构中被减去
    • 这里的光线数量不包括之前已经减去的 occluder 挡住的光线
      • 神奇？怎么实现？

3.4 本文的贡献

  • 我们可以处理局部的可见性（两个多边形之间）
  • 对于大部分场景，算法都能很快停止
  • 一般场景而言，比全局的可见性算法快，近似复杂度 \(n^{2.4}\)

4. query architecture

  • 我们希望能够对多边形进行分组，这样便能够对着一组多边形进行有效的查询
  • 我们也想用到之前计算得到的结果

4.1 Cluster Queries

  • 我们使用简单的两层结构组织场景
    • 场景由物体组成，物体由多边形组成
    • 如果物体很大，我们将其拆解为多个小物体
      • 物体体积、多边形个数
  • source cell to object query
    • 先对这个物体的包围盒进行一个可见性判断，6x6 个组合
      • 全返回不可见则这个物体不可见
      • 一个返回可见则物体有可能可见，对其中的多边形进行判断

4.2 Parent Line-space Reuse

  • 在进行 source cell to object query 的时候，我们获得了到包围盒上可见的直线集合，那么如果一个多边形想要可见，必然要和这个集合有相交的部分
    • 这可以作为一个检测

4.3 Virtual Occluders

  • virtual occluders are occluders that are not part of the geometry, but still represent a set of blocked lines.
  • 如果包围盒的一个面不可见的话，这可以被用来当作是之后物体的 occluder
  • 如果在判定的时候，我们发现一个物体的包围盒不可见，那么我们可以用这个包围盒代替其中的物体作为一个 occluder
  • 在处理场景的时候，我们大致使用从前向后的顺序去处理，因此可以用上上面的策略