(论文)[SIG-2005] Energy redistribution path tracing

Posted on Edited on In Views:
ERPT 将 MLT 结合到 PT 的框架下。和 MLT 的区别主要有两点。初始样本使用像素的 MC 采样，使得结果无偏；能量沉积方式不同，效果更好

ERPT

  • Energy redistribution path tracing

  • MLT 近似分布，ERPT 将其结合到 PT 框架下，保留了其变异的好处

  • 我看 mitsuba0.6 的实现

    • MLT 是随机采样若干个样本，然后使用 MLT 进行变异（变异次数 \(~200000\)）
    • ERPT 是为每一个像素生成一个样本，然后进行能量重新分配（分配次数 \(100\times\) numChains）

  • 有一个非常简单的实现，基于 cpu smallpt

  • 和 MLT 的区别

    • erpt 很多短链，mlt 长链
    • 初始样本使用所有像素的 MC 采样【mlt 是屏幕空间采样若干样本，然后再在其中重采样】，使得无偏
    • 能量沉积方式不同，erpt 每次沉积当前光路的能量的固定比例【mlt 每次沉积平均 luminance】
      • 其实就是平均 luminance x 常数

Introduction

  • GI 算法
    • PT：Importance sampling
    • BDPT
    • Irradiance caching、density estimation、PM
    • MLT
      • 增加变异策略，处理参与介质
      • PSSMLT
      • 处理 start-up bias
      • 方差分析
  • ERPT
    • MLT 在低维空间下收敛性还不如 PT【例如 DI】
    • 我们使用更短的 sample chains【pt 的样本消除了 startup-bias】

Sampling Issues

\[ \int_{\Omega} f(\bar{x}) \, \mathrm{d}\mu(\bar{x}) \]

  • MC

\[ \mathbf{X}_f(\bar{x}) = \frac{f(\bar{x})}{p(\bar{x})}\tag{1} \]

  • 定义：expected energy

\[ \mathbf{X}_f(\bar{x})p(\bar{x}) = f(\bar{x})\tag{2} \]

  • Correlated Integrals
    • 像素之间有相关性
    • 算法：irradiance caching、MLT、PM

Energy Flow

  • energy：这里定义为 real-valued function，这里指的是积分的 luminance
  • energy flow 有效
    • 例如下图两个相关的积分，如果能建立 \(\bar{x},\bar{y}\) 之间的关系，那么将能平摊开销，提高效率

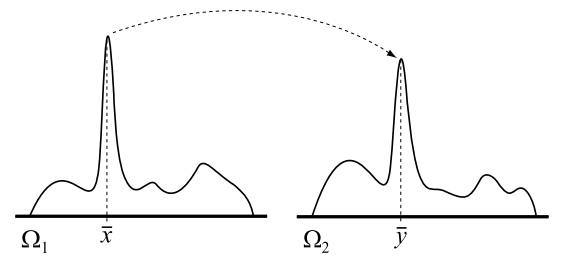
  • expected energy flow
    • source point \(\bar{x}\)，destination point \(\bar{y}\)
    • transition probability $ T({x} {y})$
    • expected energy \(\mathbf{X}_f(\bar{x})p(\bar{x})\)
    • 传递能量的百分比 \(q(\bar{x} \to \bar{y})\)

\[ E[\phi(\bar{x} \to \bar{y})] = E[\mathbf{X}_f(\bar{x}) \, p(\bar{x}) \, T(\bar{x} \to \bar{y}) \, q(\bar{x} \to \bar{y})]\tag{3} \]

  • 如果满足如下式子，则是无偏
    • 传入等于传出
    • 称为 general balance

\[ E\left[\int \phi(\bar{x} \to \bar{y}) \, d\mu(\bar{y})\right] = E\left[\int \phi(\bar{y} \to \bar{x}) \, d\mu(\bar{y})\right] \quad \forall \bar{x}\tag{4} \]

  • 更强的细致平衡条件（detailed balance）
    • general balance 的充分条件

\[ E\left[\phi(\bar{x} \to \bar{y})\right] = E\left[\phi(\bar{y} \to \bar{x})\right] \quad \forall \bar{x},\bar{y}\tag{5} \]

​

Metropolis Sampling

  • 回顾，Metropolis algorithm / Metropolis-Hastings algorithm
  • 局限
    • MLT 说从平稳分布中采样，但是没有显示构建这个分布
    • startup bias
    • 收敛很难分析
    • 不好和 PT 结合【PT 的很多改进没法用】
  • ER Samping
    • 保留 mutation
    • 没有 startup bias
    • 可以作为 PT 的插件

ER Sampling

  • 两步算法
    • 第一步：获取 MC 样本
    • 第二步：energy flow 重新分配

  • 结果中做实验对比了 3 种情况

Detailed Balance Flow Rule

  • initial attempt：使用 MLT 的细致平衡定义 \(q\)

\[ q(\bar{x} \to \bar{y}) = \min\left(1, \frac{\mathbf{X}_f(\bar{y}) p(\bar{y}) T(\bar{y} \to \bar{x})}{\mathbf{X}_f(\bar{x}) p(\bar{x}) T(\bar{x} \to \bar{y})}\right)\tag{6} \]

  • MLT 里面的 \(f(\bar{x})\) 指的是 MC 估计，所以我感觉这里其实是这个

\[ q(\bar{x} \to \bar{y}) = \min\left(1, \frac{\mathbf{X}_f(\bar{y}) T(\bar{y} \to \bar{x})}{\mathbf{X}_f(\bar{x}) T(\bar{x} \to \bar{y})}\right)\tag{6'} \]

  • 流程
    • 对 \(\bar{x}\) 进行变异 \(n\) 次形成样本 \(\bar{y}_1,\cdots,\bar{y}_n\)（应该不是一个序列，都是从 \(\bar{x}\) 变异形成）
    • \(\bar{y}_i\) 的累计贡献：\(\mathbf{X}_f(\bar{y})/n\)
  • 问题
    • 如果 \(f(\bar{x})\) 很大，那么能量流不出去；方差依然很大
  • 递归处理：复杂度很高
    • \(\bar{x}\) 第一次变异生成样本 \(\bar{x},\bar{y}_i\)（因为只转移了部分）
    • 继续变成树状结构了，复杂度高

Equal Deposition Flow Rule

  • 线性复杂度：构建 linear Markov chains【转移的时候全转移或者全不转移，依照概率，期望上和上面一样】
  • 注意 sample chains 需要一样长，才能保持无偏
    • 【应该是因为累计时候需要 \(/n\) 的问题】
  • 每次变异的时候都保存相同的能量值 \(e_d\)【方法命名原因】

  • 总的能量
    • stochastic rounding 不用管，相当于期望数是 \(e/(m\times e_d)\)
    • 总能量：\(e_d\times numChains\times m=e/(m\times e_d)\times m=e\)
  • 特殊情况
    • 所有的样本一开始 energy 如果是一样的，那么 ERPT 的过程和 MLT 一样（但是没有 startup bias）
  • deposition energy \(e_d=e_{ave}/m\)
    • \(e_{ave}\)：一系列 MC 获取的样本的能量平均值【估计】
      • 不好的估计只会影响效率，不会影响正确性
      • 和 MLT 里面的全局 luminance scale 类似，这里相当于估计了一个每次变异分配的能量，每轮变异分配 \(e_{ave}\)
    • \(m\)：设定的变异次数（短链 \(m\approx100\)）
      • mlt：\(\approx200000\)

ERPT

  • 下面几段（或者说这一整章）其实和 MLT-impl 没什么区别了

Ray Paths and Monte Carlo Path Density

  • light direction：\(\Theta\)
  • view direction：\(\Psi\)

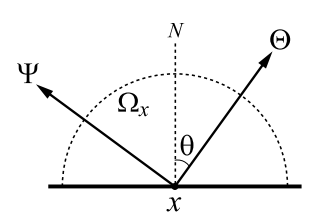\[ L(x \to \Psi) = L_e(x \to \Psi) + \int_{\Omega_x} L(x \leftarrow \Theta) f_r(\Psi \leftrightarrow \Theta) |\cos \theta| \, \mathrm{d}\omega_{\Theta} \tag{8} \]

  • 击中光源
    • explicit path：NEE ray
    • implicit path：BSDF ray
  • \(p_d\)：采样出射方向的 pdf
  • BSDF ray
    • \(p_{length}\) 表示采样长度 \(n\) 的概率【不太懂怎么控制，现在似乎都没有这一项，不管就好了】

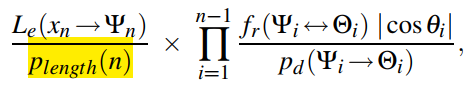
  • NEE ray（和 MLT-impl 一样多了 \(\pi\)，感觉可能是当时的定义不太一样）

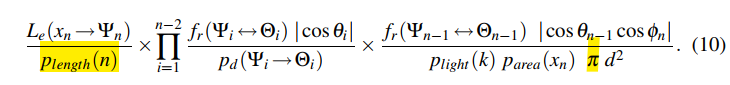
  • path density：所有采样 pdf 的累乘

Mutation and Changes in Path Density

  • 需要计算变异前后的 path density 的比值【算 \(q\) 需要】
    • \(p(\bar{y})/p(\bar{x})\)
  • 根据 MLT-impl 论文中的规则扩展【那篇论文主要针对 diffuse，采样 pdf 为余弦采样】
  • Rule 1：Changes to pixel coordinates
    • 像素采样概率相同，因此显式改变像素位置，不改变 pdf
  • Rule 2：Changes to directions
    • 很直观，算一下就 ok
    • 镜面是因为有 Fresnel 项

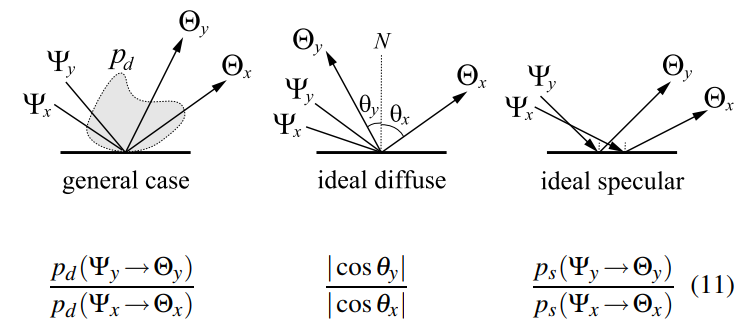
  • Rule 3：Connecting points in the middle of a path
    • 面积采样，都是余弦采样：变化正比于 \(|\cos\theta_1\cos\theta_2/d^2|\)
    • 方向采样的话：把 \(\cos\theta_1\) 修改为方向采样 \(p_d\) 就行
      • 对吗？方向的话是不是还得把 \(d^2\) 也处理下

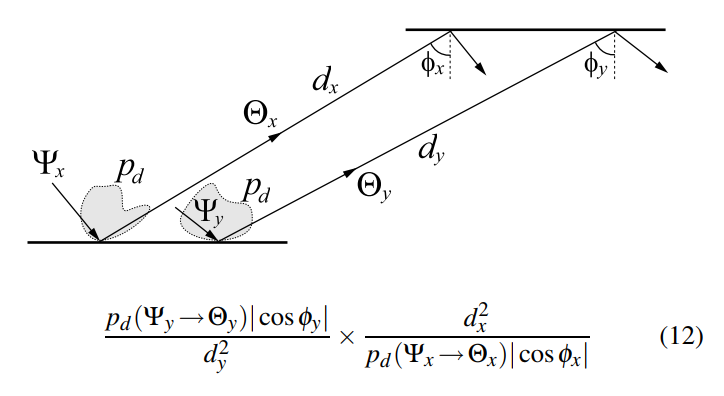
  • Rule 4：Connecting points to light sources
    • NEE ray：光源均匀采样的话，不变
    • BSDF ray：和 rule3 类似
  • Rule 5：Connecting a point to the viewer
    • 正比于：\(|\cos\theta_2/(\cos\theta^3_1d^2)|\)
    • 结果就是变化前后除一下

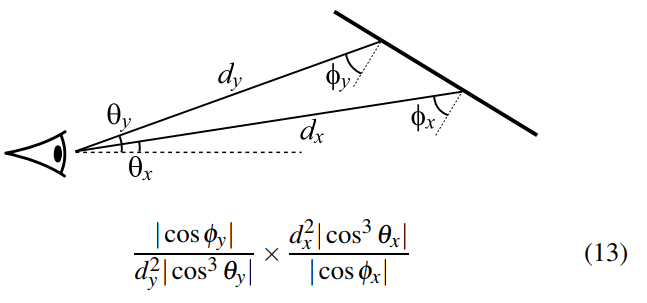
  • 反正结果上就是，要求这个样本的 pdf 和 MC 过程生成的一样一样

Mutation Strategies

  • 两种策略
    • Lens perturbations
    • caustic perturbations
  • Lens perturbations
    • 像素平面扰动
    • 追相同跳数+类型的 speculr vertex
    • 如果 \(\bar{x}\) 下一个节点 non-specular，则连他，结束；否则两边都继续前进，直到能连或者碰到光源
  • Caustic perturbations
    • 起始扰动在光源、或者从 eye 开始的第二个 diffuse vertex
  • 选择：对 \(L\dots SDE\) 使用 caustic perturbation，其他使用 lens perturbation
    • 选择方式不唯一，我们用这个

Noise Filtering

  • 两种有偏的后处理，没太看懂为啥好，mitusba 的实现版本也没管这个【因为有偏】
  • Proposed mutations noise filtering
  • Consecutive sample filtering【防止能量过度集中在某一点导致斑点噪声】
    • 变异的时候，如果连着 \(m\) 个样本都是一样的话，接下来的相同样本不累计贡献
    • 样本序列：\(y_1,\cdots,y_m,y_{m+1},\cdots,y_{m+n},y_{m+n+1},\cdots\)
      • 如果：\(y_1=\cdots=y_{m+n}\)，那么这里只累计前 \(m\) 个样本的贡献，忽略后 \(n\) 个；之后因为 \(y_{m+n}\ne y_{m+n+1}\)，所以累计
      • 相当于限制最大连续相同样本为 \(m\)（10/20）

Results

  • Flow Rule
    • Detailed Balance Flow Rule 效果不好
    • Recursive Detailed Balance Flow Rule 效果还习惯，但是慢
    • Equal Deposition Flow Rule 效果好
  • chain length：100-1000 不错
    • 短的话，收敛不一致
    • 长的话，失去了一开始 MC 样本的好处【stratification】
    • 结果图：ref，10，100

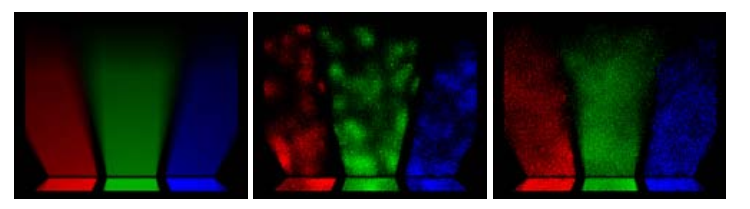
  • MLT 和 ERPT 大部分场景中表现类似
    • 变异次数少的时候，ERPT 更好（能量分布更好？
    • 没太懂这句话意思
      • However, ERPT tends to stratify a little better over the image plane

后续工作

  • 更好的 flow 规则
  • ER 样本和 MC 样本的比例

无偏证明

  • 首先 erpt 消除 startup bias 的方式就是用全屏的 MC 样本代替了 mlt 的随机采样+重采样
    • 确实这就和 mlt 初始采样大量样本相似
  • 如果已经达到了细致平衡，和这里证明类似：首先结果是正比于 \(f(x_{pixel})\) 的
    • 相当于每次累计 \(1\) 换成了 \(e_d\)，然后因为 color 转 luminance，需要沉积归一化后的 luminance x \(e_d\)
  • 然后因为沉积的时候，\(e_d\) 是除以 spp 的，所以结果就是恰好是 \(f(x_{pixel})\)【不需要归一化了】
  • mlt 最终的归一化【应该称为 scale？】其实就是除以 spp

其他

simpleerpt

  • 仓库
  • \(e_d\) 的计算：1spp 所有像素的颜色值的平均值
  • 它的实现是在 primary space 进行的
    • 具体的来说记录初始路径所用的所有随机数（vector 记录）
    • 变异的时候对这些随机数进行变异
  • 两步实现：MCPT 生成初始样本 + ERPT
  • MCPT
    • 每个像素追一条光线，记录所用的随机数和最终贡献
    • 如果是直接光，则不变异，直接累计
  • ERPT：（非直接光）
    • 分配能量，就是按照上面的实现方式
      • 加了连续样本滤波【有偏】
    • primary space：变成就是 luminance
      • 转移概率相同，都是随机扰动
      • 转移函数和 mlt 一样，\(f(\bar{x})\) 指的是 MC估计的值

\[ q(\bar{x} \to \bar{y}) = \min\left(1, \frac{f(\bar{y}) T(\bar{y} \to \bar{x})}{f(\bar{x}) T(\bar{x} \to \bar{y})}\right)\tag{6} \]

mitsuba0.6 实现

  • 回顾一下 mitsuba0.6 里面 MLT 的实现
    • 然后就可以看到，区别就是上面说的两点
    • 转移函数用的和 mlt 也是一样的

​