(论文)[1997] Metropolis Light Transport
- VEACH E., GUIBAS L. J.: Metropolis light transport. In Annual Conference Series (Proceedings of SIGGRAPH) (Aug. 1997), vol. 31, ACM Press, pp. 65–76. doi:10/bkjqj4.
TODO 找时间得继续看看
Metropolis Light Transport
Abstract
- We present a new Monte Carlo method for solving the light transport problem, inspired by the Metropolis sampling method in computational physics.
- MLT 是无偏的
- Our algorithm is unbiased, handles general geometric and scattering models, uses little storage, and can be orders of magnitude more efficient than previous unbiased approaches.
- 优点
- 在复杂场景中表现很好
- bright indirect light
- small geometric holes
- glossy surfaces.
- 简单场景中和之前的方法相比也不错
- 在复杂场景中表现很好
- The key advantage of the Metropolis approach is that the
path space is explored locally, by favoring
mutations that make small changes to the current path
- First, the average cost per sample is small (typically only one or two rays).
- Second, once an important path is found, the nearby paths are explored as well, thus amortizing the expense of finding such paths over many samples.
- Third, the mutation set is easily extended. By constructing mutations that preserve certain properties of the path (e.g. which light source is used) while changing others, we can exploit various kinds of coherence in the scene. It is often possible to handle difficult lighting problems efficiently by designing a specialized mutation in this way.
1 Introduction
- current methods are optimized for a fairly narrow class of input scenes.
- Monte Carlo methods
- generality and simplicity.
- unbiased
- For these algorithms, any error in the solution is guaranteed to show up as random variations among the samples (e.g., as image noise).
- 有偏算法带来的问题
- Biased algorithms may produce results that are not noisy, but are nevertheless incorrect.
- This error is often noticeable visually, in the form of discontinuities, excessive blurring, or objectionable surface shading.
- Monte Carlo 算法的问题
- The problem is that for some environments, most paths do not contribute significantly to the image, e.g. because they strike surfaces with low reflectivity, or go through solid objects.
- 出问题的场景
- For example, imagine a brightly lit room next to a dark room
containing the camera, with a door slightly ajar between them.
- 两个房间,光源在一个房间中,相机在另一个房间中,两个房间之间有一扇半开的门
- For example, imagine a brightly lit room next to a dark room
containing the camera, with a door slightly ajar between them.
- 对如下现象都不太支持
- glossy surfaces, caustics, strong indirect lighting
- Several techniques have been proposed to sample these difficult
paths more efficiently.
- bidirectional path tracing (BDPT)
- Another idea is to build an approximate representation of
the radiance in a scene, which is then used to modify
the directional sampling of the basic path tracing algorithm.
- 一些问题
- inadequate directional resolution to handle concentrated indirect lighting
- substantial(大量) space requirements.
- MLT
- The algorithm samples paths according to the contribution they make to the ideal image, by means of a random walk through path space.
2 Overview of the MLT algorithm
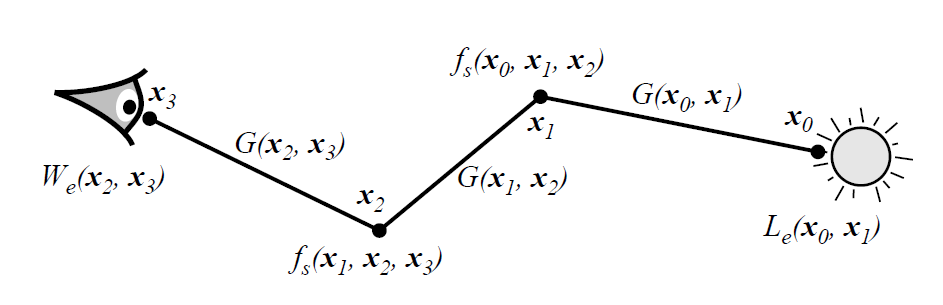
- sample the paths from the light sources to the lens
- path \(\bar{x}=\mathrm{x}_0\mathrm{x}_1\cdots\mathrm{x}_k\)
- \(\mathrm{x}_0\) 是光源
- 长度 \(k\ge1\)
- power (flux) that flows from the light sources to the image plane along a set of paths \(D\).
\[ \int_{D}f(\bar{x})\;d\mu(\mathrm{x}) \]
- \(f\):image contribution function
- Our overall strategy is to sample paths with probability proportional to \(f\), and record the distribution of paths over the image plane
- We generate a sequence of paths \(\bar{X}_0,\bar{X}_1,\cdots,\bar{X}_N\), where each \(\bar{X}_i\) is obtained by a random mutation to the path \(\bar{X}_{i-1}\)
- The mutations can have almost any desired form
- adding, deleting, or replacing a small number of vertices on the current path
- each mutation has a chance of being rejected, depending on the relative contributions of the old and new paths.
- As each path is sampled, we update the current image
- 算法如下

3 The Metropolis sampling algorithm
In 1953, Metropolis, Rosenbluth, Rosenbluth, Teller, and Teller introduced an algorithm for handling difficult sampling problems in computational physics
前提
- We are given a state space \(\Omega\), and a non-negative function \(f:\Omega\to \mathbb{R}^+\).
- We are also given some initial state \(\bar{X}_0\in\Omega\)
目标
- generate a random walk \(\bar{X}_0,\bar{X}_1,\cdots,\bar{X}_N\) such that \(\bar{X}_i\) is eventually distributed proportionally to \(f\), no matter which state \(\bar{X}_0\) we start with.
the Metropolis algorithm does not require that \(f\) integrate to one.
Each sample \(\bar{X}_i\) is obtained by making a random change to \(\bar{X}_{i−1}\)
- in our case, these are the path mutations
马尔科夫链
- This type of random walk, where \(\bar{X}_i\) depends only on \(X_{i−1}\), is called a Markov chain.
We let \(K(\bar{y}|\bar{x})\) denote the probability density of going to state \(\bar{y}\), given that we are currently in state \(\bar{x}\).
- transition function
- satisfies the condition
\[ \int_{\Omega}K(\bar{y}|\bar{x})\;d\mu(\bar{y})=1,\forall\bar{x}\in\Omega \]
The stationary distribution
- 平稳分布(状态不变)
- Each \(\bar{X}_i\) is a random variable with some distribution \(p_i\), which is determined from \(p_{i−1}\) by the equation (1) With mild conditions on \(K\)
\[ p_{i}(\bar{x})=\int_{G}K(\bar{x}|\bar{y})\;p_{i}(\bar{y})\;d\mu(\bar{y})\qquad(1) \]
- the \(p_i\) will converge to a unique distribution \(p\), called the stationary distribution
- Note that p does not depend on the initial state \(\bar{X}_0\)
Detailed balance
- 细致平衡
- 在实际的物理系统中,\(K\) 是由物理约束决定的,给定初始状态便会变化到平稳分布
- The Metropolis algorithm works in the opposite
direction.
- The idea is to invent or construct a transition function \(K\) whose resulting stationary distribution will be proportional to the given \(f\), and which will converge to \(f\) as quickly as possible.
- 找到转移函数 \(K\) ,希望他能够快速收敛到 \(f\)
- The technique is simple, and has an intuitive physical interpretation called detailed balance.
- Given \(\bar{X}_{i-1}\), we obtain \(\bar{X}_i\) as follows.
- First, we choose a tentative(试探性的) sample \(X_i'\)
- This is represented by the tentative transition function \(T\)
- where \(T(\bar{y}|\bar{x})\) gives the probability density that \(X_i'=\bar{y}\) given that \(X_i'=\bar{x}\)
- The tentative sample is then either accepted or rejected, according to an acceptance probability \(a(\bar{y}|\bar{x})\) which will be defined below
\[ X_i= \begin{cases} X_i' \qquad \mathrm{with\;probability\;a(\overline{X}_i'|\overline{X}_{i-1}})\\ X_{i=1} \quad \mathrm{otherwise} \end{cases} \]
- To see how to set \(a(\bar{y}|\bar{x})\), suppose that we have already reached equilibrium, i.e. \(p_{i−1}\) is proportional to \(f\).
- From \(\bar{x}\) to \(\bar{y}\), the transition density is proportional to \(f(\bar{x})\;T(\bar{y}|\bar{x})\;a(\bar{y}|\bar{x})\), and a similar statement holds for the transition density from \(\bar{y}\) to \(\bar{x}\).
- 细致平衡条件
\[ f(\bar{x})\;T(\bar{y}|\bar{x})\;a(\bar{y}|\bar{x})=f(\bar{y})\;T(\bar{x}|\bar{y})\;a(\bar{x}|\bar{y}),\qquad (3) \]
- 细致平衡条件是平稳分布的充分条件
\[ \begin{aligned} p_{i}(\bar{x})=&\Big[1-\int_{\Omega}f(\bar{x})\;T(\bar{y}|\bar{x})\;a(\bar{y}|\bar{x})\;d\mu(\bar{y})\Big]p_{i-1}(\bar{x})\qquad(4)\\ &+\int_{\Omega}f(\bar{x})\;p_{i-1}(\bar{y})T(\bar{x}|\bar{y})\;a(\bar{x}|\bar{y})\;d\mu(\bar{y})\\ &=p_{i-1}(\bar{x})\\ \end{aligned} \]
The acceptance probability
接受概率
Recall that \(f\) is given, and \(T\) was chosen arbitrarily. Thus, equation (3) is a condition on the ratio \(a(\bar{y}|\bar{x})/a(\bar{x}|\bar{y})\).
In order to reach equilibrium as quickly as possible, the best strategy is to make \(a(\bar{x}|\bar{y})\) and \(a(\bar{y}|\bar{x})\) as large as possible
\[ a(\bar{y}|\bar{x})=\min\Big\{1,\dfrac{f(\bar{y})T(\bar{x}|\bar{y})}{f(\bar{x})T(\bar{y}|\bar{x})}\Big\} \]
- According to this rule, transitions in one direction are always accepted, while in the other direction they are sometimes rejected, such that the expected number of moves each way is the same.
Comparison with genetic algorithms
- different purposes
- genetic algorithms solve optimization problems
- while the Metropolis method solves sampling problems
- Genetic algorithms work with a population of individuals, while Metropolis stores only a single current state.
- Finally, genetic algorithms have much more freedom in choosing the allowable mutations, since they do not need to compute the conditional probability of their actions
4 The path integral formulation of light transport
- Often the light transport problem is written as an integral equation, where we must solve for the equilibrium radiance function L.
- However, it can also be written as a pure integration
problem, over the domain of all transport
paths.
- The MLT algorithm is based on this formulation.
The light transport equation
- We assume a geometric optics model where light is emitted, scattered, and absorbed only at surfaces, travels in straight lines between surfaces, and is perfectly incoherent.
- light transport equation
- \(\mathcal{M}\) is the union of all scene surfaces
- \(A\) is the area measure on \(\mathcal{M}\)
- The function \(G\) represents the throughput of a differential beam between \(dA(\mathrm{x})\) and \(dA(\mathrm{x'})\)
\[ L(\mathrm{x'}\to\mathrm{x''})=L_e(\mathrm{x'}\to\mathrm{x''})+\int_{\mathcal{M}}L(\mathrm{x}\to\mathrm{x'})f_s(\mathrm{x}\to\mathrm{x'}\to\mathrm{x''}){\color{red}G(\mathrm{x}\leftrightarrow\mathrm{x'})}\;dA(\mathrm{x}) \]
- \(G\) 如下
- where \(\cos\theta_o\) and \(\cos\theta_i'\) represent the angles between the segment \(\mathrm{x}\leftrightarrow\mathrm{x'}\) and the surface normals at \(\mathrm{x}\) and \(\mathrm{x_0}\) respectively
- \(V\) 为可见性
\[ G(\mathrm{x}\leftrightarrow\mathrm{x'})=V(\mathrm{x}\leftrightarrow\mathrm{x'})\dfrac{|\cos\theta_o\cos\theta_i'|}{\Vert\mathrm{x}-\mathrm{x'}\Vert^2} \]
The measurement equation
- We consider only algorithms that compute an image directly, so that the measurements consist of many pixel values \(m_1,\cdots,m_M\), where M is the number of pixels in the image.
- Each measurement has the form
\[ m_j=\int_{\mathcal{M}\times\mathcal{M}}W_e^{(j)}(\mathrm{x}\to\mathrm{x}')L(\mathrm{x}\to\mathrm{x}')G(\mathrm{x}\leftrightarrow\mathrm{x}')\;dA(\mathrm{x})\;dA(\mathrm{x}') \]
- where \(W_e^{(j)}(\mathrm{x}\to\mathrm{x'})\)
is a weight that indicates how much the light arriving at \(\mathrm{x'}\) from the direction of
\(\mathrm{x}\) contributes to the value
of the measurement
- For real sensors, \(W_e^{(j)}(\mathrm{x}\to\mathrm{x'})\) is called the flux responsivity (with units of \([W^{-1}]\)), but in graphics it is more often called an importance function
The path integral formulation
- By recursively expanding the transport equation (6), we can write measurements in the form
\[ \begin{aligned} m_j=&\int_{\mathcal{M}^2}L(\mathrm{x}_0\to\mathrm{x}_1)G(\mathrm{x}_0\leftrightarrow\mathrm{x}_1)W_e^{(j)}(\mathrm{x}_0\to\mathrm{x}_1)\;dA(\mathrm{x}_0)\;dA(\mathrm{x}_1)\\ &+\int_{\mathcal{M}^3}L(\mathrm{x}_0\to\mathrm{x}_1)G(\mathrm{x}_0\leftrightarrow\mathrm{x}_1)f_s(\mathrm{x}_0\leftrightarrow\mathrm{x}_1\leftrightarrow\mathrm{x}_2)G(\mathrm{x}_1\leftrightarrow\mathrm{x}_2)W_e^{(j)}(\mathrm{x}_1\to\mathrm{x}_2)\;dA(\mathrm{x}_0)\;dA(\mathrm{x}_1)\;dA(\mathrm{x}_2)\\ &\cdots\\ \end{aligned} \]
- The goal is to write this expression in the form, so that we can handle it as a pure integration problem.
\[ m_j=\int_{\Omega}f_j(\bar{x})\;d\mu(\bar{x}) \]
- let \(\Omega_k\) be the set of all paths of the form \(\bar{x}=\mathrm{x}_0\mathrm{x}_1\cdots\mathrm{x}_k\), where \(k\ge1\) and \(x_i\in\mathcal{M}\) for each \(i\).
\[ d\mu_k(\mathrm{x}_0\cdots\mathrm{x}_k)=dA(\mathrm{x}_0)\cdots\;dA(\mathrm{x}_k) \]
- we let \(\Omega\) be the union of
all the \(\Omega_k\) and define a
measure \(\mu\) on \(\Omega_k\) by
- 感觉可以把 \(D\) 理解为路径全空间
\[ \mu(D)=\sum_{k=1}^{\infty}\mu_k(D\;\cap\Omega_k) \]
- We call \(f_j\) the measurement contribution function
- 例子
\[ f_j(\mathrm{x}_0\mathrm{x}_1)=L_e(\mathrm{x}_0\to\mathrm{x}_1)G(\mathrm{x}_0\leftrightarrow\mathrm{x}_1)W_e^{(j)}(\mathrm{x}_0\to\mathrm{x}_1) \]

- 上面转化的目的
- The most significant aspect is that we have removed the sum over different path lengths, and replaced it with a single integral over an abstract measure space of paths.
5 Metropolis light transport
- 一些准备工作
- First, we must formulate the light transport problem so that it fits the Metropolis framework.
- Second, we must show how to avoid start-up bias, a problem which affects many Metropolis applications.
- Most importantly, we must design a suitable set of mutations on paths, such that the Metropolis method will work efficiently.
5.1 Reduction to the Metropolis framework
- Observe that each integrand \(f_j\)
has the form \(f_j(\bar{x})=w_j(\bar{x})f(\bar{x})\)
- \(w_j\) represents the filter function for pixel \(j\)
- \(f\) represents all the other factors of \(f_j\) (which are the same for all pixels).
- In physical terms, \(\int_Df(\bar{x})\;d\mu(\bar{x})\) represents the radiant power received by the image area of the image plane along a set \(D\) of paths.
- Note that \(w_j\) depends only on the last edge \(\mathrm{x}_{k-1}\mathrm{x}_k\) of the path, which we call the lens edge.
- An image can now be computed by sampling \(N\) paths \(\mathrm{X}_i\) according to some distribution \(p\), and using the identity
\[ m_j=E\Big[\dfrac{1}{N}\sum_{i=1}^{N}\dfrac{w_j(\bar{X}_i)f(\bar{X}_i)}{p(\bar{X}_i)}\Big] \]
- If we could let \(p=\dfrac{1}{b}f\) (where \(b\) is the normalization constant \(\int_\Omega f(\bar{x})\;d\mu(\bar{x})\), the estimate for each pixel would be
\[ m_j=E\Big[\dfrac{1}{N}\sum_{i=1}^{N}b\;w_j(\bar{X}_i)\Big] \]
- This equation can be evaluated efficiently for all pixels at once, since each path contributes to only a few pixel values.
- 问题:This idea requires the evaluation of \(b\), and the ability to sample from a
distribution proportional to \(f\).
- Both of these are hard problems.
- For the second part, the Metropolis algorithm will
help
- however, the samples \(\bar{X}_i\) will have the desired distribution only in the limit as \(i\to\infty\)
- Metropolis 应用中丢弃前 k 个 sample,直到结果大概收敛到 equilibrium
distribution
- k 的预测也是个问题
- start-up bias:如果选取的 k 太小,结果将很大程度上受到 \(\bar{X}_0\) 的影响
Eliminating start-up bias
- The idea is to start the walk in a random initial state \(\bar{X}_0\), which is sampled from
some convenient path distribution \(p_0\)
- we use bidirectional path tracing for this purpose
- 初始路径通过其他采样方式采出
- To compensate for the fact that \(p_0\) is not the desired distribution \(\dfrac{1}{b}f\), the sample \(\bar{X}_0\) is assigned a weight: \(W_0=\dfrac{f(\bar{X}_0)}{p_0(\bar{X}_0)}\)
- Thus after one sample, the estimate for pixel \(j\) is \(W_0w_j(\bar{X}_0)\)
- N=1 代入即可
- \(\bar{X}_0\) 已知的条件下,这些都是可以计算的
- 接下来可以根据 Metropolis algorithm 进行采样得到 \(\bar{X}_1,\cdots,\bar{X}_N\)
- mutating \(\bar{X}_0\)
- using \(f\) as the target density
- Each of the \(\bar{X}_i\) has a different distribution \(p_i\), which only approaches \(\dfrac{1}{b}f\) as \(i\to\infty\)
- To avoid bias, however, it is sufficient to assign these samples the same weight \(W_i=W_0\) as the original sample, where the following estimate is used for pixel \(j\)
\[ m_j=E\Big[\dfrac{1}{N}\sum_{i=1}^{N}w_j(\bar{X}_i){W_i}\Big] \]
- unbiased
- 如果 \(p_0=\dfrac{1}{b}f,W_0=b\),那么结果一定是 equilibrium.
- 对于一般的 \(p_0\)
- \(W_0=\dfrac{f}{p_0}\) leads to exactly the same distribution of weighta mong the starting paths, and so we should expect that these initial conditions are unbiased as well.
- unbiased 证明如下
- 首先证明如下等式在每一步中都成立
\[ \int_{\mathbb{R}}w\;q_i(w,\bar{x})\;dw=f(\bar{x}) \]
- where \(q_i\) is the joint probability distribution of the i-th weighted sample \((W_i,\bar{X}i)\)
- \(q_0\) 是成立的
- \(q_0(w,\bar{x})=\delta(w-\dfrac{f(\bar{x})}{p_0(\bar{x})})p_0(\bar{x})\)
- \(\delta\) denotes the Dirac delta distribution
- \(W_0=\dfrac{f(\bar{X}_0)}{p_0(\bar{X}_0)}\)
- \(q_0(w,\bar{x})=\delta(w-\dfrac{f(\bar{x})}{p_0(\bar{x})})p_0(\bar{x})\)
- 由上面的等式 (4)
- Next, observe that (4) is still true with \(p_j\) replaced by \(q_i(w,\bar{x})\) (since the mutations set \(W_i=W_{i−1}\)).
- \(\int_{\mathbb{R}}w\;q_i(w,\bar{x})\;dw=\int_{\mathbb{R}}w\;q_{i-1}(w,\bar{x})\;dw\)
\[ \begin{aligned} E\Big[w_j(\bar{X}_i){W_i}\Big]&=\int_{\Omega}\int_{\mathbb{R}}w\;w_j(\bar{x})\;q_i(w,\bar{x})\;dw\;d\mu(\bar{x})\\ &=\int_{\Omega}\;w_j(\bar{x})\;f(\bar{x})\;d\mu(\bar{x})\\ &=m_j\\ \end{aligned} \]
- 期望计算:\(E(XY)=\iint xyf(x,y)dxdy\)
Initialization
- In practice, initializing the MLT algorithm with a single sample does not work well
- If we generate only one path \(\bar{X}_0\) (e.g. using bidirectional path
tracing), it is quite likely that \(W_0=0\) (e.g. the path goes
through a wall).
- 结果为全黑
- The strategy we have implemented is to sample a moderately large number of paths \(\bar{X}_0^{(1)},\cdots,\bar{X}_0^{(n)}\), with corresponding weights \(W_0^{(1)},\cdots,W_0^{(n)}\)
- We then resample the \(\bar{X}_0^{(i)}\) to obtain a much smaller
number \(n'\) of equally-weighted
paths
- chosen with equal spacing in the cumulative weight distribution of the \(\bar{X}_0^{(i)}\)
- These are used as independent seeds for the Metropolis phase of the algorithm
- The value of n is determined indirectly, by generating a fixed
number of eye and light subpaths (e.g. 10000 pairs), and considering all
the ways to link the vertices of each pair.
- Note that it is not necessary to save all of these paths for the resampling step
- they can be regenerated by restarting the random number generator with the same seed.
- It is often reasonable to choose \(n'=1\) (a single Metropolis seed).
- 实际测试中,初始化这一步的开销很小
- two phase
- The initialization phase estimates the overall image brightness
- while the Metropolis phase determines the relative pixel intensities across the image
Convergence tests
- Another reason to run several copies of the algorithm in parallel is
that it facilitates(促进) convergence testing.
- We cannot apply the usual variance tests to samples generated by a single run of the Metropolis algorithm, since consecutive samples are highly correlated.
- To test for convergence, the Metropolis phase runs with \(n'\) independent seed paths, whose contributions to the image are recorded separately (in the form of \(n'\) separate images).
Spectral sampling
- Effectively, each color component \(h\) is sampled with an estimator of the form \(h/p\), where \(p\) is proportional to the luminance.
5.2 Designing a mutation strategy
- MLT 的问题
- consecutive samples are correlated, which leads to
higher variance than we would get with independent
samples.
- 连续被拒绝导致存在未收敛的相同样本,影响 variance
- This can happen either because the proposed mutations to the path are very small, or because too many mutations are rejected.
- consecutive samples are correlated, which leads to
higher variance than we would get with independent
samples.
- This problem can be minimized by choosing a suitable set of path mutations.
- 一些 mutation 需要具备的特征
- High acceptance probability
- acceptance probability is small \(\to\) long path sequences \(\to\) many samples at the same point on the image plane \(\to\) appears as noise
- Large changes to the path
- small mutations 还是可能会导致 highly correlated
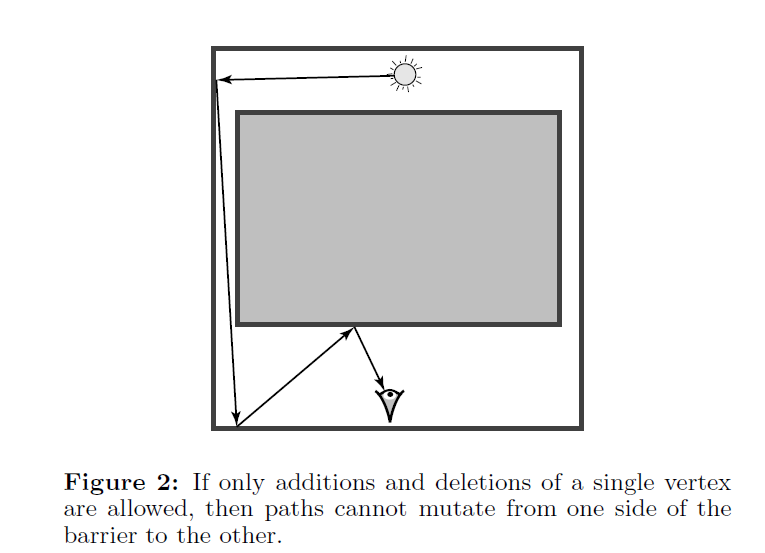
- Ergodicity
- If the allowable mutations are too restricted, it is possible for
the random walk to get " in some subregion of the path space.
- 比如下面的 figure 2
- To minimize correlation between the sample locations on the image plane, it is desirable for mutations to change the lens edge \(\mathrm{x}_{k-1}\mathrm{x}_{k}\)
- If the allowable mutations are too restricted, it is possible for
the random walk to get " in some subregion of the path space.
- Stratification
- This is commonly known as the "balls in bins" effect:
- if we randomly throw n balls into n bins, we cannot expect one ball per bin.
- Many bins may be empty, while the fullest bin is likely to contain \(\Theta({n\log n})\) balls
- In an image, this unevenness in the distribution produces noise.
- For some kinds of mutations, this effect is difficult to avoid.
- However, it is worthwhile to consider mutations for which some form of stratification is possible.
- This is commonly known as the "balls in bins" effect:
- Low cost
- Generally, this is measured by the number of rays cast, since the other costs are relatively small