(论文)[2020-SIG] Specular Manifold Sampling for Rendering High-Frequency Caustics and Glints

Posted on Edited on In Views:
SMS，当两个 vertex 之间存在多条 specular 路径时，能够有效求解，只能求解短路径

Specular Manifold Sampling for Rendering High-Frequency Caustics and Glints

  • Tizian Zeltner, Iliyan Georgiev, and Wenzel Jakob. 2020. Specular Manifold Sampling for Rendering High-Frequency Caustics and Glints. ACM Trans. Graph. 39, 4, Article 149 (July 2020), 15 pages. https://doi.org/10.1145/3386569.3392408
  • 效果图
    • ordinary unidirectional path tracer
    • 我们新提出的 specular manifold sampling 策略

  • our method supports
    • high-frequency normal- or displacement-mapped geometry,
    • samples specular-diffuse-specular (“SDS”) paths,
    • and is compatible with standard Monte Carlo methods including unidirectional path tracing
  • Both unbiased and biased variants of our approach can be constructed

1 INTRODUCTION

  • specular path
    • difficult to find
  • 论文的方法
    • glints and SDS paths—in an unbiased manner
  • 论文的贡献
      1. A unified manifold sampling strategy for rendering reflective and refractive caustics.**
      1. A specialized variant for rendering glints, which reduces memory usage hundred-fold compared to prior work.
      1. A biased variant of the method with reduced variance.
      1. A two-pass sampling strategy for normal-mapped surfaces.
      1. Changes to the specular manifold constraints of Jakob and Marschner [2012] that improve robustness and convergence.
  • 问题
    • variance increases significantly for longer specular chains, hence our experiments mainly focus on short chains with 1 or 2 vertices.

2 PRIOR WORK

  • path tracing
  • photon mapping
  • Newton-Raphson iteration
  • tree structure
  • 论文的参考算法
    • Our algorithm is closely related to Jakob and Marschner’s manifold exploration (ME) method [2012], which is a Markov chain Monte Carlo (MCMC) perturbation strategy that analyzes the differential geometry of the manifold of valid specular paths to make proposals in the framework of Metropolis Light Transport [Veach 1998].
  • MNEE
    • Starting with an incorrect initial specular path, MNEE iteratively attempts to walk towards a valid solution via projection and tangential steps on the specular manifold.
    • 最多找到一个解
  • 论文算法
    • The proposed method, named specular manifold sampling (SMS), is a generalization of the MNEE approach: using a stochastic initialization and an unbiased sampling weight estimator, we are able to find solutions on complex geometry where manifold-based techniques were previously inapplicable.
      • 论文的算法是 MNEE 的泛化，能够解决复杂几何形体表面的路径采样问题
    • We also propose a simple 2-stage stochastic initialization for normal-mapped surfaces and demonstrate that SMS straightforwardly generalizes to the related problem of glint rendering.We provide a brief review

3 BACKGROUND

  • light transport path
    • \(\bar{\mathrm{x}}=\mathrm{x}_0,...,\mathrm{x}_n\)
    • 端点 \(\mathrm{x}_1,\mathrm{x}_n\) non-specular
    • 中间路径是 specular 的
    • 下图是一个例子：\(\mathrm{x_n}\) 是光源

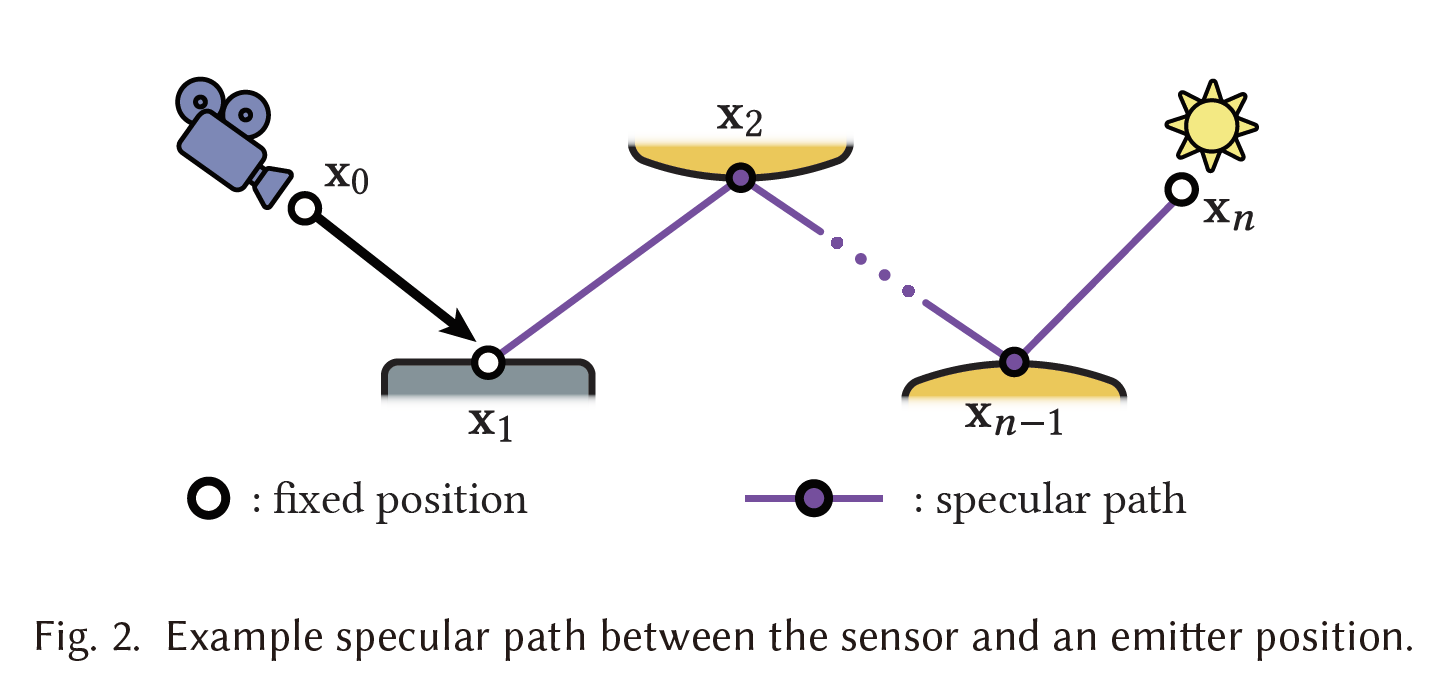
  • Snell' law：折射定律
  • 上述路径的约束条件
    • \(T(x_i)\) is a 3 × 2 matrix of tangent vectors
    • 向量都归一化了

\[ \mathrm{c}_i(\mathrm{x}_{i-1},\mathrm{x}_i,\mathrm{x}_{i+1})=\mathrm{T}(\mathrm{x}_i)^T\mathrm{h}(\mathrm{x}_i,\overrightarrow{\mathrm{x}_i\mathrm{x}_{i-1}},\overrightarrow{\mathrm{x}_i\mathrm{x}_{i+1}})\;\;\;(1) \]

  • 联立
    • \(\mathrm{C}(\bar{x})=[\mathrm{c}_2,...,\mathrm{c}_{n−1}]^T\)
    • The function is normally parameterized via the UV coordinates \(\mathrm{uv}_i\) of specular vertices,
  • 求解
    • \(\mathrm{C}(\mathrm{\overline{uv}})=0\)
    • 牛顿迭代法求解：\(\mathrm{\overline{uv}}_{i+1}=(\nabla\mathrm{C}(\mathrm{\overline{uv}}_i))^{-1}\cdot\mathrm{C}(\mathrm{\overline{uv}}_i)\)

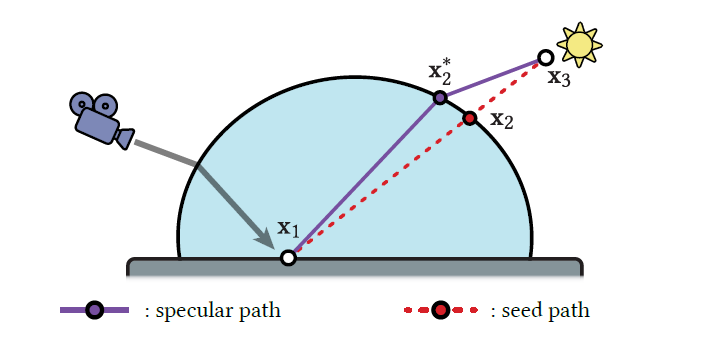
3.1 Manifold next-event estimation(MNEE)

  • 问题
    • 简单形体有效
      • spheres or cylinders
      • where a single solution indeed suffices to render most specular paths.
    • 不知道怎么初始化
      • refractive caustics 可以（Hanika et al.），但是不知道怎么推广到折射
    • Finally, MNEE does not support paths that give rise to specular glints.
  • 算法

4 METHOD

  • pecular manifold sampling (SMS)
    • initially focusing on a simple unbiased algorithm that generalizes to cases where multiple specular paths connect two given endpoints.
  • 几种扩展算法（模块化、可随意组装的）
    • the first reduces variance at the cost of nonzero bias
    • the second replaces Jakob and Marschner’s specular manifold constraints with improved variants,
    • the third samples paths in two stages to improve performance on normal-mapped surfaces, and the last streamlines the algorithm for glint rendering.
  • 组装例子

4.1 Finding all solutions

  • 初始化
    • We initially restrict ourselves to specular chains with a single smooth reflection or refraction.
  • 思路
    • whereas MNEE performs manifold walks using a fixed initialization, SMS randomly samples the initial guess from a probability distribution \(p(\overline{\mathrm{x}}_0)\).
    • Newton’s method exhibits quadratic convergence when the starting point is sufficiently close to a root, hence all solutions will be found with a nonzero probability—however, the probability of successful convergence is unknown.
  • 初始化选择的自由度很高
    • we assume that the implementation of this sampling strategy takes two uniformly distributed random numbers \(\xi (\xi_1,\xi_2)\in [0,1)^2 =:\mathcal{U}\) as input and warps them to the desired distribution.
    • 目标是使得初始的采样路径 \(\xi\) 离正确的结果比较近，这样牛顿法才有效
  • When inspecting the convergence behavior of these manifold walks on the primary sample space \(\mathcal{U}\), we generally observe multiple basins of convergence \(\mathcal{B}_k\subseteq \mathcal{U}\), each containing a point \(\xi^{k}\) identified with a corresponding solution vertex \(x_2^{(k)}\).
  • Fig. 4.
    • (a): Multiple solutions of the specular path constraint form a superposition of caustics in the Ring scene.
    • (b): Color map showing the number of solutions at each shading point.
    • (c): The three solution paths at a particular point.
    • (d): The basins of convergence (in primary sample space) corresponding to those solution paths. All manifold walks started at a point (black dot) inside a region converge to the associated solution (colored dot).

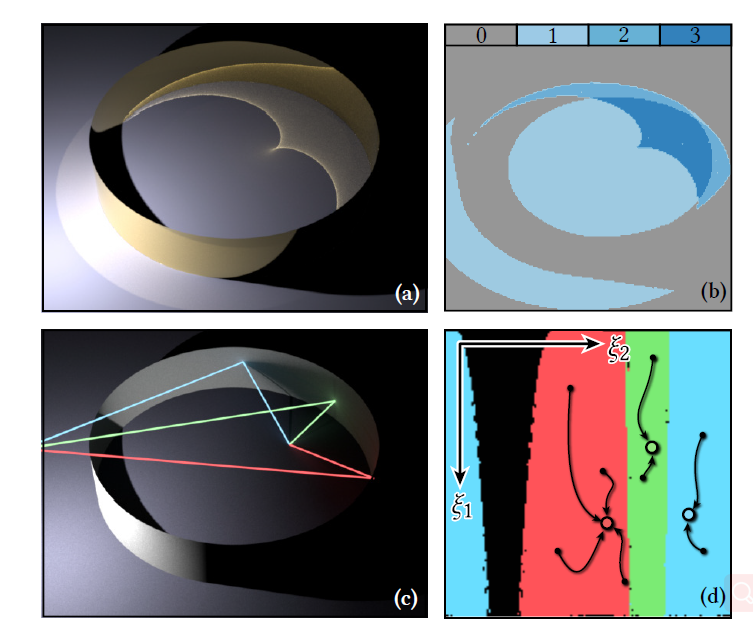
  • Newton’s method is known to produce convergence basins that potentially have an extremely complex geometric structure [Hubbard et al. 2001] and can even be fractal.
  • An unbiased estimator is then given by a standard MC ratio \(\dfrac{f(\overline{x})}{p(\overline{x})}\)
  • Since the samples \(\xi\) are uniformly distributed, this probability is simply the area of the associated convergence basin on \(\mathcal{U}\)

\[ p_k=\int_{\mathcal{U}}\mathbb{1}_{\mathcal{B}_k}(\xi)\;\mathrm{d}\xi \]

  • 但是这个是不可行的，\(\mathcal{B}_k\) 可能有复杂的几何结构
  • 简单的无偏估计如下

\[ \langle p_k\rangle=\dfrac{1}{N}\sum_{i=1}^N\mathbb{1}_{\mathcal{B}_k}(\xi) \]

  • 这个估计存在一些问题 \(\mathbb{E}[\dfrac{1}{X}]\ne\dfrac{1}{\mathbb{E}[X]}\)
    • 引入 bias
    • for example, \(\langle p_k\rangle\) can equal zero if all N tries fail to converge to the basin \(\mathcal{B}_k\)
      • \(\langle \dfrac{1}{p_k}\rangle\to\infty\)
  • Fortunately, an unbiased estimator for the inverse ⟨1/pk ⟩ can be created using a simple iterative approach.

4.2 Unbiased SMS

  • turning the inverse into a geometric series(几何级数) moves the problematic integral from the denominator(分母) to the numerator(分子)

\[ \dfrac{1}{p_k}=\dfrac{1}{\int_{\mathcal{U}}\mathbb{1}_{\mathcal{B}_k}(\xi)\;\mathrm{d}\xi}=\dfrac{1}{1-a}=\sum_{i=0}^{\infty}a^i \]

\[ a=1-\int_{\mathcal{U}}\mathbb{1}_{\mathcal{B}_k}(\xi)\;\mathrm{d}\xi,\;|a|<1 \]

  • 那么就会有

\[ \langle\dfrac{1}{p_k}\rangle=1+\sum_{i=1}^{\infty}\prod_{j=1}^{i}\langle a\rangle_j \]

  • \(\langle a\rangle_j=0\) when manifold walk \(j\) has converged to root \(\xi_k\)
  • \(\langle a\rangle_j=1\) if it has found another root or diverged
  • Unbiased SMS is trivially added to any existing implementation of MNEE.
  • 算法如下

  • 复杂度和几何形体相关
    • when the geometry is complex, many solutions may exist, and their convergence basins also occupy smaller area in primary sample space.
  • 方差
    • Furthermore, the variance of such an estimator for a specific solution pk based on a geometric distribution is equal to \(\dfrac{1-p_k}{p_k^2}\) , which can become very large when \(p_k\approx 0\).

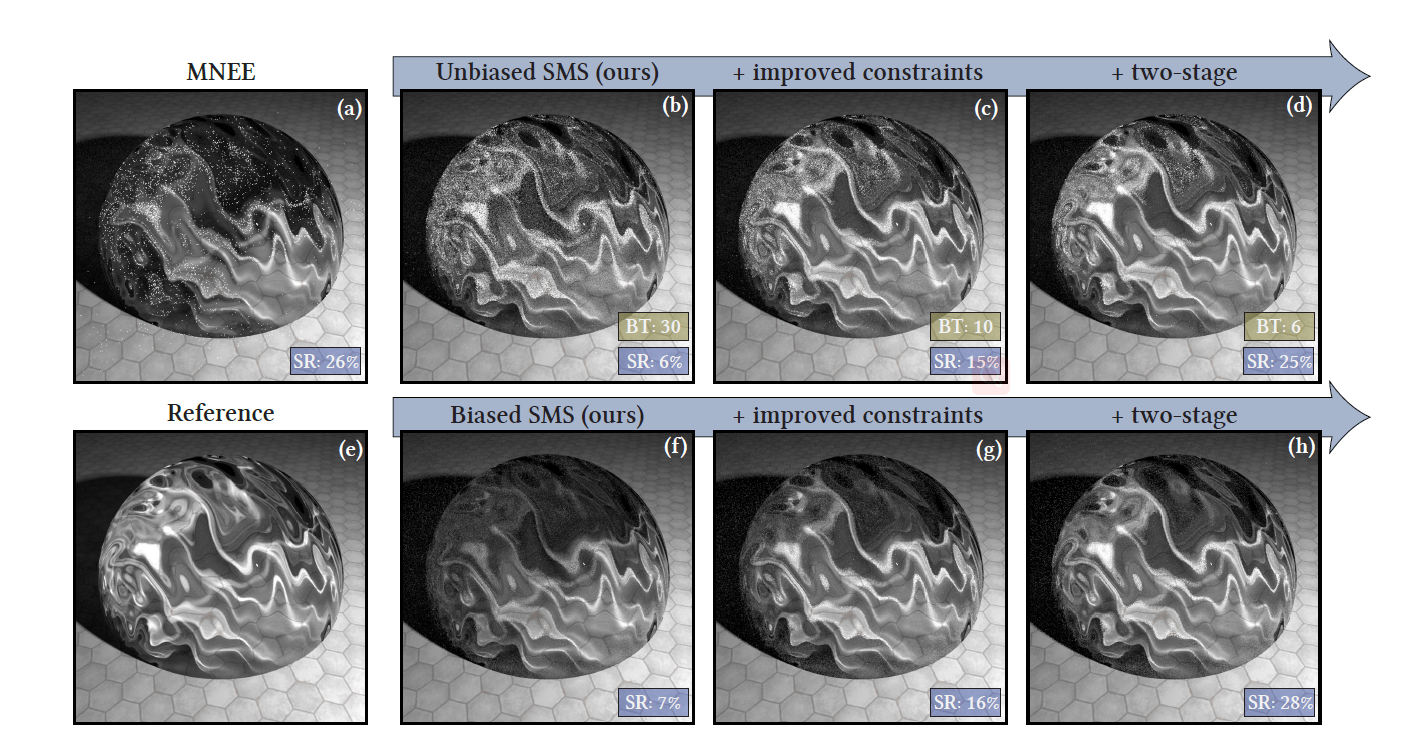
4.3 Biased SMS

  • 引入 bias，但是同时降低了 variance，减小了运行时间
  • The biased variant of our method (Alg. 3) replaces the unbounded number of trial iterations by a fixed budget of M samples.
  • we simply cluster the M samples into a set of unique solutions \(\mathrm{x}_2^{(l)}(l = 1,\cdots, L)\).
  • A biased estimate of the reciprocal is then given by the relative number of occurrences nl of each solution, which also avoids the potential issues with a division by zero discussed earlier.

\[ \dfrac{1}{M}\sum_{l=1}^{L}n_l\dfrac{f(\mathrm{x}_2^{(l)})}{p(\mathrm{x}_2^{(l)})}\approx\dfrac{1}{M}\sum_{l=1}^{L}n_lf(\mathrm{x}_2^{(l)})\dfrac{M}{n_l}=\sum_{l=1}^{L}f(\mathrm{x}_2^{(l)}) \]

  • Compared to the original unbiased approach, this variant has a fixed iteration count, and it exploits the information provided by all samples.
  • 有偏但是是一致的
    • Note that it is consistent and will converge to the true solution as \(M\to\infty\)
  • 论文中 bias 体现为能量损失
    • In our experiments, we observe that the resulting bias is manifested as energy loss
    • 焦散很暗
  • 算法如下

  • MNEE 和 biased SMS
    • When setting \(M=1\), biased SMS is closely related to a biased version of MNEE where no MIS is applied to account for paths that cannot be sampled using the manifold walk.
    • 但是是不等价的
    • Consider a situation where only one valid solution exists but the straight-line initialization doesn’t converge to it.
      • In this case, MNEE can produce arbitrarily high variance—or in case of point lights will miss the contribution entirely.
      • SMS however will still find the solution with non-zero probability.
  • 向量化并行
    • modern SIMD instruction sets, such as AVX512.

4.4 Improved specular manifold constraints

  • One significant difference of our method compared to all previous applications of manifold walks is that we require the Newton solver to take very large steps starting from an invalid state.
    • MNEE renders refractive caustics with a straight-line initialization that is generally already very close to the final solution.
    • applications of manifold walks to MCMC rendering [Jakob and Marschner 2012; Lehtinen et al. 2013] only make small perturbations to existing valid paths
  • 因此上述的两种方法收敛很快
  • 我们的方法到现在为止，随机的初始化导致收敛很慢（即使是在简单的集合外形上也出现问题）
    • manifold walks would often converge surprisingly poorly when initialized randomly
  • 导致收敛出现问题的原因
    • when taking large steps, Newton iterations based on the original specular manifold constraints often produce invalid back-facing solutions that impede convergence.
    • back-facing：下图中的 invalid 路径，光照从内部反射，这是不可能的
  • The main issue here is how the specular manifold constraint in Eq. (1) encodes specular configurations via half-vector projections.
  • While this term conveniently subsumes both reflective and refractive cases with one equation, the formulation does not distinguish between front- and back-facing solutions

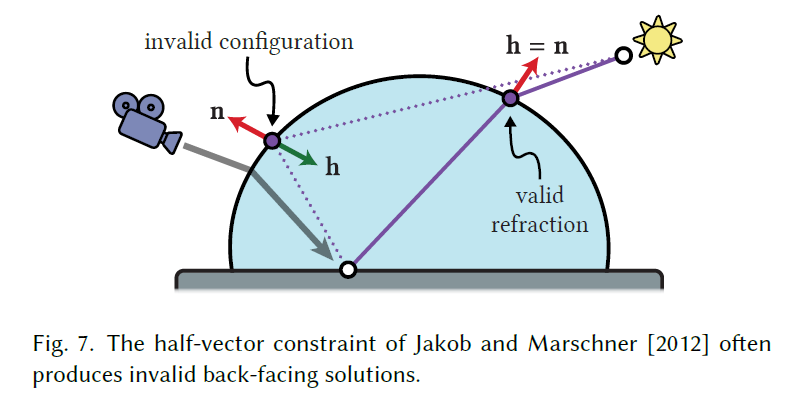
  • 我们提出了一个新的约束条件，区分折射和反射
    • scattered direction \(S(\omega,\mathrm{n},\eta)\)
    • incident direction \(\omega\)
    • surface normal \(\mathrm{n}\)

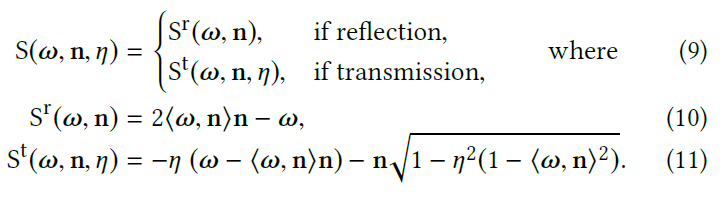
  • 度量条件：\(\mathrm{\omega}_o=S(\omega_i,\mathrm{n},\eta)\)
    • 具体我们使用 \(2\mathrm{D}\) 度量方式（实验发现效果比较好）
    • we therefore measure a difference in the spherical coordinates of both vectors

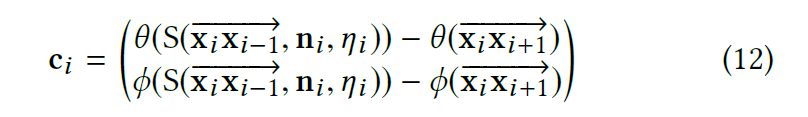
  • \(\theta(\omega) = \cos^{−1}(\omega_z)\)
  • \(\phi(\omega)=\mathrm{atan}\;2(\omega_y,\omega_x)\)
  • 一个其他问题
    • Note that the scattering operation \(\mathrm{S}(\cdot)\) can fail in configurations with total internal reflection.
    • In such cases we are still able to evaluate the constraint for the opposite light direction by taking the difference between \(\mathrm{\omega}_o\) and \(S(\omega_i,\mathrm{n},\eta)\)

4.5 Two-stage manifold walks

  • we observe that the more complex caustic is a superposition(叠加) of many different solutions with a fairly localized effect(局部效应)
  • The space \(\mathcal{U}\) is largely empty, containing only a few small convergence basins that are clustered together. The probability of finding a valid solution is therefore low.
    • 采样概率小

  • Furthermore, estimating the reciprocal probability depends on our ability to find the same solution once more, which is even less likely.
  • Unbiased SMS estimates therefore tend be slow and noisy, while biased SMS loses a considerable amount of energy.
    • 采样概率小导致的问题
  • 为了解决上述问题，我们提出一种利用先验知识找初始路径的方法。
  • consider a caustic generated by a smooth planar surface(光滑平面产生的焦散)
    • 我们观察到，当表面的几何结构不太复杂时，焦散都是有一个比较大的收敛域产生的
    • 当表面几何结构变得复杂的时候，大的收敛域分割为多个小的收敛域
  • Our two-stage sampling approach performs two manifold walks
    • the first stage ignores the specified normal map and finds specular paths on the original smooth surface.
      • Such a smooth manifold walk will converge to a point that roughly lies at the center of the cluster of solutions
      • 具体使用的策略：offset manifold walk [Jakob and Marschner 2012]
    • a second manifold walk, on the bumpy surface, started from there takes us all the way to a solution.

4.6 Glints

  • Our method generalizes straightforwardly to the problem of rendering glints, which are miniscule subpixel reflections of a light source with narrow angular support (e.g. the sun) on high-frequency specular microgeometry.
  • 标准的 MC 方法开销太大
    • millions of samples per pixel may be needed to obtain an acceptable result
  • Our method generates random starting points within the pixel and then runs unbiased or biased SMS to find solutions
  • 之前的方法
    • introduced a small amount of intrinsic roughness to relax the problem
  • we solve the unmodified problem with a discrete set of solutions to find a path \(\mathrm{\bar{x}}=\mathrm{x} _0,\mathrm{x}_1,\mathrm{x}_2\) connecting the camera to a sampled emitter position via a single specular reflection.
    • 单次反射
  • 一些和之前一样的假设
    • Like prior work, we assume that the endpoints \(\mathrm{x} _0\) and \(\mathrm{x} _2\) are distant, in which case changes in the half-vector across the parallelogram are minimal.
  • 这些假设简化搜索
    • in particular, the specular manifold constraint can be simplified to a function that attempts to equate this fixed half-vector and the local shading normal, both expressed in 2D slope space.
  • 泛化与鲁棒性
    • To robustly apply our glint rendering technique in scenes with complex lighting (e.g. high-frequency environment maps), we further combine our SMS strategy with standard BSDF sampling in a multiple importance sampling (MIS) framework.
    • 效果很好

4.7 Integration into rendering algorithms

5 RESULTS

  • 详见论文

6 CONCLUSION

  • Our article focuses mainly on the generation of subpaths with a single specular vertex.
  • While our method in principle also generalizes to more complex path classes with multiple specular reflection, performance using our current strategy for choosing starting points remains suboptimal and could be an interesting topic for future work.