(论文)[2023-SIG-Course] A Gentle Introduction to ReSTIR: Path Reuse in Real-time (3)

Posted on In Views:
ResTIR GI，如何在 PT 中重采样一条路径，如何做 shift mapping

ReSTIR

  • 主页
  • update：March 4, 2024

06-ReSTIR Path Tracing

  • 路径空间积分形式
    • 从 DI 扩展出来

\[ L(\mathbf{x}_{1}\to\mathbf{x}_{0})=\sum_{D=2}^{\infty}\int_{\mathcal{A}^{D-1}}\Big(\prod_{j=1}^{D-1}f_{s}(\mathbf{x}_{j+1}\to\mathbf{x}_{j}\to\mathbf{x}_{j-1})G(\mathbf{x}_{j}\leftrightarrow\mathbf{x}_{j+1})V(\mathbf{x}_{j}\leftrightarrow\mathbf{x}_{j+1})\Big)L_{e}(\mathbf{x}_{D}\to\mathbf{x}_{D-1}) \mathrm{d}\mathbf{x}_{2}\ldots\mathrm{d}\mathbf{x}_{D} \]

  • 路径：\(D-1\) bounce

\[ [{\color{red}\mathrm{x}_{0},\mathrm{x}_{1}},\mathrm{x}_{2},\mathrm{x}_{3},\cdots,\mathrm{x}_D] \]

RIS with a path tracer

  • NEE 开启之后，会形成 path tree
    • RIS：选取一整条路径
  • 只考虑 NEE 的 RIS
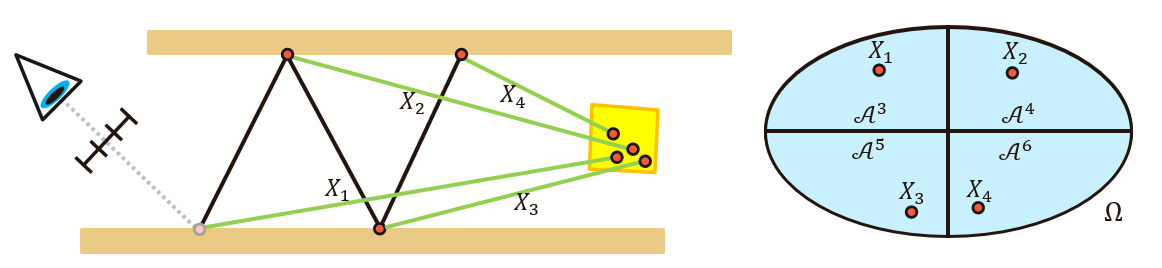
    • RIS 过程：重新采样一个顶点 \(x\in\{x_2,x_3,x_4,x_5\}\)（\(x_1\) 则表示 \(X_1\) 这条 NEE ray）
    • \(w_{i}=m_{i}(x_{i})\hat{p}(x_{i})W_{x_{i}}\)
      • \(m_i(x_i)=1\)，互斥，形成的光路长度不一样，属于不同的路径子空间
        • 例如 \(x_1\)，则是 \(X_1\) NEE ray，则整条光路长度为 3
      • \(\hat{p}(x_{i})=f(x_i)\)、\(W_{x_{i}}=\dfrac{1}{p(x_i)}\)：这些在 PT 框架下都有容易获取

  • 如果考虑所有的光路作为 RIS 的候选，则需要考虑一条路径可能同时被 NEE、BSDF（常规 PT）采样得到
    • 那么 \(m_i(x_i)\) 此时 \(\le1\)
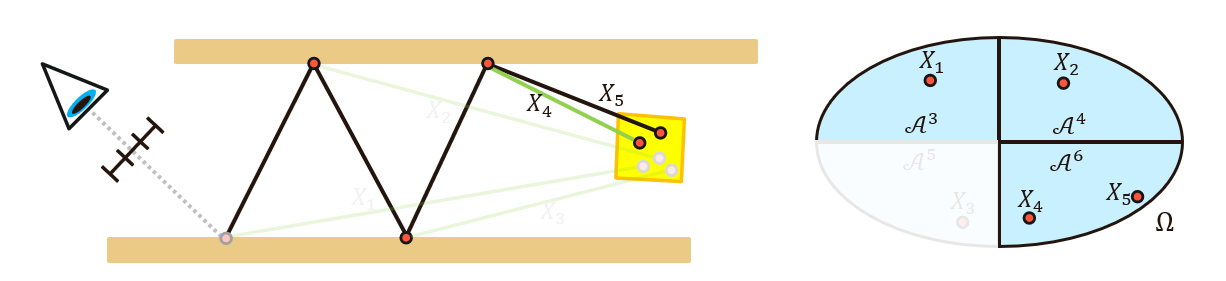
    • 例如下图中，\(X_4,X_5\) 的 mis 将会 <1

Reuse path samples

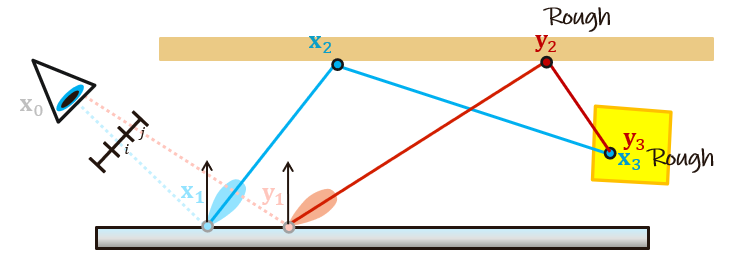
  • 最简单的方式：identity shift（area measure）

\[ T([{\color{gray}x_0,x_1},x_2,\ldots,x_D])=[{\color{gray}y_0,y_1},x_2,\ldots,x_D] \]

  • 重连 \(y_1,x_2\)
    • 重新计算 BSDF 贡献、几何项、可见性项（发射 shadow ray）
  • biasd 版本：加速、减少内存开销
    • 认为 \(\overline{x_2y_1}\) 近似等于 \(\overline{x_2x_1}\)：少数情况下效果不错
  • specular 的复用问题很大

Good shift mapping

  • good：假定每一个像素都有一个比较好的重要性采样 \(p_X\approx \bar{p}\)，理想的形式应该是 shift mapping 之后生成的样本和 \(p_X\) 类似
    • 下式：对于 \(i\) 像素的一个好的 shift mapping

\[ \bar{p}_j(T(x))\left\vert\frac{\partial T}{\partial x}\right\vert\approx\bar{p}_i(x) \]

  • identity shift（area measure）：如果 \(x_2\) 是 diffuse 的话，这是容易满足的
    • 但是如果 \(\overline{x_2y_1}\) 、\(\overline{x_2x_1}\) 距离相差太远，几何项差太多，那么结果也不好

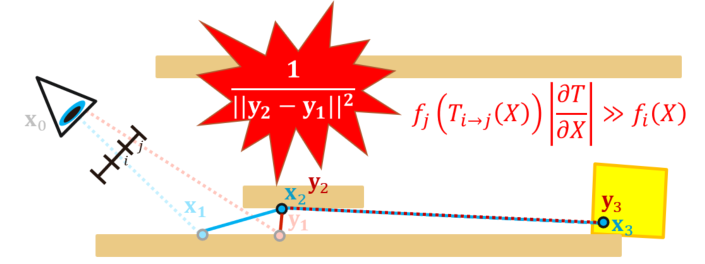
  • 如果 \(x_1/y_1/x_2\) 存在 specular，这样效果就很差
    • 如下图，黑色高贡献，但是蓝色几乎贡献为 0

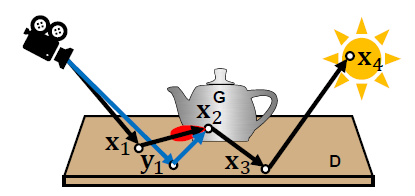
Common shift mappings

  • 借鉴 gradient domain rendering
  • 假设相邻像素变化小
    • 那么相邻相像素 \(i,j\) 的 \(\hat{p}\) 归一化因子类似
    • 假设 \(\hat{p}\approx f\)
    • 于是 good shift mapping 条件如下

\[ f_j(T(x))\left\vert\frac{\partial T}{\partial x}\right\vert\approx f_i(x) \]

  • 和 gradient domain rendering 用的条件一样，可以参考它所用的 shift mapping
  • Half-vector shift
    • 对于 specular，拷贝对应点（\(k\)）的 tangent-space half-vector，直到 \(y_k\) 和 \(x_{k+1}\) 能够连接
    • 双射要求 \(y_k,x_{k+1}\) 都是 diffuse（roughness 大于给定值）
    • 出发点：尽可能保留相近的 throughput
      • 当处理 bounce 数变多（多次连不上），产生大的 divergence，效果不太好
    • 合适的材质，效果不错
  • 目的：preserve the path contribution

Efficient shift mapping for RTR

  • hybrid shift
    • random replay
    • additional distance condition
    • 只根据采样 lobe 的 roughness 进行顶点分类
  • 优点
    • 存储小：一个重连接的顶点、随机数种子
    • glossy/refraction 材质效果好
  • 目的：为了保持贡献相近

Ensuring Invertibility

两个条件

  • Distance Condition（为什么不是比例）
    • 第 2 个是为了保证可逆

\[ \min(\Vert\mathrm{x}_k-\mathrm{x}_{k-1}\Vert,\Vert\mathrm{x}_k-\mathrm{y}_{k-1}\Vert)\geq d_{\min} \]

  • Roughness Condition（足够粗糙，这样对重连接友好）
    • \(\ell\)：表示采样到的 lobe
      • 如果存在多个 lobe，则 \(\ell=\mathop{\arg\max}_{\ell}\alpha(\ell)\)
    • \(\alpha\)：roughness（specular \(\to\) diffuse：\(0\to1\)）

\[ \min(\alpha_{\mathrm{x}_{k-1}}(\ell_{k-1}),\alpha_{\mathrm{y}_{k-1}}(\ell_{k-1}^{\prime}),\alpha_{\mathrm{x}_{k}}(\ell_{k}))\geq\alpha_{\min} \]

流程

  • 在 base path 形成的过程中（PT），满足如下两个条件的最小 \(k(k\ge2)\) 对应的节点 \(\mathrm{x}_k\) 被保存为 reconnection vertex

\[ \Vert\mathrm{x}_k-\mathrm{x}_{k-1}\Vert\ge d_{\min},\min(\alpha_{\mathrm{x}_{k-1}}(\ell_{k-1}),\alpha_{\mathrm{x}_{k}}(\ell_{k}))\geq\alpha_{\min} \]

  • shift 的时候，使用 random replay（相同的随机数种子生成路径）生成 offset path，直到 \(\mathrm{y}_{k-1}\) 和 \(\mathrm{x}_{k}\) 相连
    • 为了可逆，同时需要满足 \(\Vert\mathrm{x}_k-\mathrm{y}_{k-1}\Vert\ge d_{\min},\min(\alpha_{\mathrm{y}_{k-1}}(\ell_{k-1}),\alpha_{\mathrm{x}_{k}}(\ell_{k}))\geq\alpha_{\min}\)
    • \(\ell'_{k-1}=\ell_{k-1}\)，直接复制
      • 如果 \(\mathrm{y}_{k-1}\) 上不存在 \(\ell_{k-1}\) 这个 lobe，那么 shift 失败
  • 不存在更小的 \(k'<k\) 满足上述条件（指 base&offset path），否则违反可逆
    • 疑惑：所以上面的 \(k\) 是整体生成的还是只通过 base path 就能生成？
      • 只能是 base path 生成
    • 感觉像是 base path 生成之后，之后只能在 \(k\) 处重连接

Path Samples with Lobe/Technique Tags

  • 为了满足 path space 到 primary sample spaces (for the random number sequence) 的双射，需要将路径扩展到带 lobe 的

\[ \bar{\mathrm{x}}=[{\color{gray}\mathrm{x}_0,(\mathrm{x}_1,}\ell_1),(\mathrm{x}_2,\ell_2),\ldots,(\mathrm{x}_{D-1},\ell_{D-1}),\mathrm{x}_D] \]

  • \(0\le\ell_j\le N_{\text{lobe}}\) 表示 \(\mathrm{x}_j\) 采样到的 lobe 类型
    • \(N_{\text{lobe}}\) is the total number of lobes in the scene
  • 如果光源被 NEE 采样得到，\(\ell_{D-1}=N_{\text{lobe}}\) 标识这个信息
  • 如此便能通过random replay 完全复现这条路径
    • 要求使用的随机数除了路径生成，不用于其他
  • 重写：长度 \(D+1\) 的路径
    • \(\bar{\ell}=\left[\ell_1,\ell_2,\cdots,\ell_{D-1}\right]\in\mathcal{L}_{D}\)
    • 上面的 \(\bar{\mathrm{x}}\in\bar{\Omega}_{D}\)
    • \(m_t(\mathrm{x})\)：NEE、BSDF 的 MIS，\(\ell_{D-1}\) 标识 NEE 还是 BSDF 采样

\[ I=\sum_{D=1}^\infty\int_{\bar{\Omega}_D}\bar{f}(\bar{\mathrm{\mathrm{x}}}) \mathrm{d}\bar{\mathrm{x}}=\sum_{D=1}^\infty\sum_{\bar{\ell}\in\mathcal{L}_D}\int_{sA^D}m_t(\mathrm{x})f_{\bar{\ell}}(\mathrm{x}) \mathrm{d}\mathrm{x} \]

Primary Sample Spaces

  • ReSTIR PT uses primary sample space(PSS) parameterization for the paths.

  • PSS 好处

    • 路径积分可以直接通过 \(f/p\) 表示，不用分开记录 \(f,p\)（浮点误差小）
    • shift mapping 过程中，random replay 的顶点 Jacobian = identity，方便计算

  • PSS 形式的路径积分

    • \(\mathbf{u}\)：随机数序列

    • \(\mathcal{U}_D=[0,1]^{\mathcal{N}(D)}\)：超立方体，\(\mathcal{N}_D\) 表示 \(\mathbf{u}\) 的长度

    • \(F(\bar{\mathbf{u}}) = \bar{f}(\mathcal{X}(\bar{\mathbf{u}}))/p(\mathcal{X}(\bar{\mathbf{u}}))\)

    • \(\mathcal{X}(\bar{\mathbf{u}})\)：映射到采样到的路径

    • \(\mathbf{u}\) 和 \(\bar{\mathrm{x}}\) 是双射

\[ I=\sum_{D=1}^\infty\int_{\mathcal{U}_D}F(\bar{\mathbf{u}})\;\mathrm{d}\bar{\mathbf{u}} \]

Jacobian 计算

  • 重连接的计算（其他的话是 identity）
  • \(\omega_{k-1}^{x}\)：\(\mathrm{x}_{k-1}\) 到 \(\mathrm{x}_{k}\) 的单位向量
  • 根据面积采样和立体角采样建立联系
    • \(\mathrm{x}_{k}=\mathrm{y}_{k}\)

\[ \left\vert\frac{\partial\omega_{k-1}^y}{\partial\omega_{k-1}^x}\right\vert =\left\vert\frac{\partial\omega_{k-1}^y}{\partial\mathrm{y}_{k}}\right\vert \cdot \left\vert\frac{\partial\mathrm{x}_{k}}{\partial\omega_{k-1}^x}\right\vert =\left\vert\frac{\cos\theta_k^y}{\cos\theta_k^x}\right\vert\frac{\Vert\mathrm{x}_k-\mathrm{x}_{k-1}\Vert^2}{\Vert\mathrm{x}_k-\mathrm{y}_{k-1}\Vert^2} \]

  • 会影响 \(\mathrm{x}_{k-1},\mathrm{x}_{k}\)
    • 如果 \(\mathrm{x}_{k}\) 是光源，则只影响 \(\mathrm{x}_{k-1}\)，红色部分为 1

\[ \left\vert\frac{\partial\bar{\mathbf{u}}^y}{\partial\bar{\mathbf{u}}^x}\right\vert= \left\vert\frac{\partial\bar{\mathbf{u}}_{k-1}^y}{\partial\bar{\mathbf{u}}_{k-1}^x}\right\vert {\color{red}\left\vert\frac{\partial\bar{\mathbf{u}}_k^y}{\partial\bar{\mathbf{u}}_k^x}\right\vert} \]

  • \(\mathrm{x}_{k-1}\)
    • \(p_{(\omega,\ell)_{k-1}^x}(\mathbf{x}_k)=p_{\omega_{k-1}^x}(\mathbf{x}_k)\cdot p_{\ell_{k-1}^x}\)：采样 lobe 和方向的联合分布，立体角度量
      • 如果是光源，那么将面积度量转化为立体角度量，lobe 采样 \(p_{\ell_{k-1}^x}=1\)
    • \(p(x)\;\mathrm{d}x=p(y)\;\mathrm{d}y\)

\[ \left\vert\frac{\partial\bar{\mathbf{u}}_{k-1}^y}{\partial\bar{\mathbf{u}}_{k-1}^{x}}\right\vert=\left\vert\frac{\partial\bar{\mathbf{u}}_{k-1}^y}{\partial\omega_{k-1}^y}\right\vert\left\vert\frac{\partial\omega_{k-1}^y}{\partial\omega_{k-1}^x}\right\vert\left\vert\frac{\partial\omega_{k-1}^x}{\partial\bar{\mathbf{u}}_{k-1}^x}\right\vert=\frac{p_{(\omega,\ell)_{k-1}^y}(\mathbf{y}_k)}{p_{(\omega,\ell)_{k-1}^x}(\mathbf{x}_k)}\left\vert\frac{\partial\omega_{k-1}^y}{\partial\omega_{k-1}^x}\right\vert \]

  • \(\mathrm{x}_{k}\)：\(\mathrm{x}_{k}=\mathrm{y}_{k}\)

\[ \left\vert\frac{\partial\bar{\mathbf{u}}_k^y}{\partial\bar{\mathbf{u}}_k^x}\right\vert=\left\vert\frac{\partial\bar{\mathbf{u}}_k^y}{\partial\omega_k^y}\right\vert\left\vert\frac{\partial\omega_k^x}{\partial\bar{\mathbf{u}}_k^x}\right\vert=\frac{p_{(\omega,\ell)_k^y}(\mathbf{y}_{k+1})}{p_{(\omega,\ell)_k^x}(\mathbf{x}_{k+1})} \]

  • 根据重连接定义：\(\omega_{k}^{x}=\omega_{k}^{y},\ell_{k-1}^{x}=\ell_{k-1}^{y}\)，但是采样概率不同（出射方向不同）

ReSTIR PT 细节

  • 数据结构如上
  • path sample 的内容
    • 重连接顶点
    • 随机数生成器（RNG），序列生成
    • 辅助信息
  • 假定重连接顶点 \(\mathrm{y}_k\) 不是光源（只是为了表示方便，处理类似）
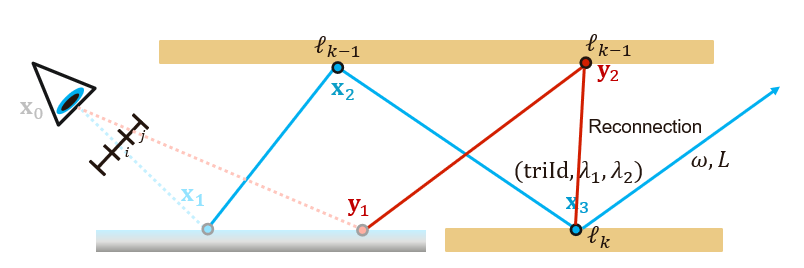
  • 重采样流程
    • RNG \(\xi_1\) 生成子序列 \(\mathrm{y}_{2},\cdots,\mathrm{y}_{k-1}\)，throughput 为 \(\beta\)
    • 通过三角形 ID（\(\Delta\)）、重心坐标 \(\lambda_1,\lambda_2\)，计算 \(\mathrm{y}_{k}=\mathrm{x}_{k}\)
      • 动态场景需要其他处理，需要使用到 \(\xi_2\)
    • \(\omega=\omega_{k}^{x}\)：入射方向，\(L\)：入射辐射度估计
    • 贡献计算如下
      • \(m_t\)：考虑到 \(\mathbf{y}_{k+1}\) 可能是光源的 MIS 系数（不是光源，则为 1）

\[ F(Y)=\hat{p}(Y)= \beta\cdot m_{t}(\omega_{k}^{y})f_{s,\omega_{k-1}^{y}}(\mathbf{y}_{k})/p_{\omega_{k-1}^{y}}(\mathbf{y}_{k})\cdot f_{s,\omega_{k}^{y}}(\mathbf{y}_{k+1})/p_{\omega_{k}^{y}}(\mathbf{y}_{k+1})\cdot L \]

  • Jacobian 根据式子计算
    • 可以预先计算一些和 \(\mathrm{y}_{k-1}\) 无关的部分保存下来，避免重复计算
  • 重采样整个算法流程如图所示
    • 蓝色 \(X_i\)，红色 \(Y_i\)

Volume rendering

  • 体渲染的积分域：\(\mathcal{M}=\mathcal{A}\cup\mathcal{V}\)
    • 表面 + 体

\[ \begin{aligned} I_{j}=&\sum_{D=1}^\infty\int_{\mathcal{M}^{D+1}}W_e^{(j)}(\mathbf{x}_1\to\mathbf{x}_0)T(\mathbf{x}_0\leftrightarrow\mathbf{x}_1)\bar{G}(\mathbf{x}_0\leftrightarrow\mathbf{x}_1)\Big(\\ &\qquad\prod_{j=1}^{D-1}\bar{f}_s(\mathbf{x}_{j+1}\to\mathbf{x}_j \to\mathbf{x}_{j-1})\bar{G}(\mathbf{x}_j\leftrightarrow\mathbf{x}_{j+1})T(\mathbf{x}_j\leftrightarrow\mathbf{x}_{j+1})\\ &\quad\Big)\bar{L}_c(\mathbf{x}_D\to\mathbf{x}_{D-1}) \;\mathrm{d}\mathbf{x}_0\mathrm{d}\mathbf{x}_1\mathrm{d}\mathbf{x}_2\ldots\mathrm{d}\mathbf{x}_D \end{aligned} \]

  • 针孔摄像机，没有相机响应函数
    • 递归形式
    • 所有点的自发光到 \(\mathrm{x}_0\) 的贡献（长度为 \(1,2,\cdots\)）
      • 疑问：这里似乎没有考虑直线外的光源？

\[ \begin{aligned}L(\omega_{0}\to \mathbf{x}_{0})&=T(\mathbf{x}_{0}\leftrightarrow \mathbf{x}_{1}^{s})(L_{e}(\mathbf{x}_{1}^{s}\to \mathbf{x}_{0})+P(\mathbf{x}_{0},\mathbf{x}_{1}^{s}))+\\&\int_{0}^{s}T(\mathbf{x}_{0}\leftrightarrow\mathbf{x}_{1})(\sigma_{a}(\mathbf{x}_{1})L_{e}^{m}(\mathbf{x}_{1}\to \mathbf{x}_{0})+P(\mathbf{x}_{0},\mathbf{x}_{1})) \mathrm{d}z_{1}\end{aligned} \]

  • \(s=||\mathbf{x}_1^s-\mathbf{x}_0||\)：最近的不透明点到像素的距离
  • \(\mathbf{x}_1=\mathbf{x}_0+z_1\omega_0\)，\(\omega_0\) 根据像素位置决定
  • \(P\)："in-scattered" path contribution

\[ \begin{aligned}P(\mathbf{x}_{0},\mathbf{x}_{1})&=\sum_{D=2}^{\infty}\int_{\mathcal{M}^{D-1}}\Big(\prod_{j=1}^{D-1}\bar{f}_{s}(\mathbf{x}_{j+1}\to\mathbf{x}_{j}\to\mathbf{x}_{j-1})\\&\bar{G}(\mathbf{x}_{j}\leftrightarrow\mathbf{x}_{j+1})T(\mathbf{x}_{j}\leftrightarrow\mathbf{x}_{j+1})\Big)\bar{L}_{e}(\mathbf{x}_{D}\to\mathbf{x}_{D-1}) \mathrm{d}\mathbf{x}_{2}\ldots\mathrm{d}\mathbf{x}_{D}\end{aligned} \]

  • 体介质
    • \(\bar{f}_s=f_s\)
    • \(\bar{G}=1/\Vert\mathbf{x}_{j}-\mathbf{x}_{j+1}\Vert^{2}\)
    • \(\bar{L}_{e}(\mathbf{x}_{D}\to\mathbf{x}_{D-1})=\sigma_{a}(\mathbf{x}_{D})L_{e}^{m}(\mathbf{x}_{D}\to\mathbf{x}_{D-1})\)
  • 表面：常规的含义
  • transmission item \(T\)
    • 计算代价高，在某些 \(\sigma\) 分段常数情况下，计算快

\[ T(\mathbf{x}\leftrightarrow\mathbf{y})=\exp\left(-\int_0^zy \sigma_t(\mathbf{x}-y\omega)\;\mathrm{d}y\right) \]

  • \(T\)：Volumetric ReSTIR 使用一个简单的 \(\hat{p}\)
    • ray marching 近似 \(T\)
    • 使用低分辨率的 volumes 计算（最小化内存开销）
    • A piece-wise constant, low resolution volume
  • Volumetric ReSTIR
    • \(\mathrm{x}_1\) 依赖于 \(z\)，复用的时候复制 \(z_1\) 去生成 shifted \(\mathrm{x}_1\)
    • 两个复用：vertex、direction
      • shifted path：\([z_1,\omega_1,z_2,\omega_2,\ldots,z_{D-1},x_D]\)
    • vertex reuse 效果好，但是由于几何上的奇异性， direction reuse 效果不佳（opted for the slower direction reuse by default）
    • 可以参考 hybrid shift（random replay、distance threshold 等）