(论文)[2023-SIG-Course] A Gentle Introduction to ReSTIR: Path Reuse in Real-time (2)
ReSTIR
- 主页
- update:March 4, 2024
04-ReSTIR
Weighted Reservoir Sampling
- Weighted reservoir sampling (WRS),一个系列
- sampling one (or more) elements from a (weighted) stream of samples in a single pass over the data without storing it
- Reservoir Resampling

- 蓄水池重采样得到的结果,恰好是满足正比于 \(w_i\) 的
- 证明
- 记 \(s_k=\sum_{i=1}^{k}w_i\),于是有 \(s_k=s_{k-1}+w_k\)
- 第 \(k\) 个样本被采样的概率如下
- 第 \(k\) 次被选中,而且之后都没有被更新
\[ \begin{aligned} \Pr(Y=X_k) =&\dfrac{w_k}{s_k}\cdot\prod_{i=k+1}^{M}\left(1-\dfrac{w_{i}}{s_{i}}\right)\\ =&\dfrac{w_k}{s_k}\cdot\prod_{i=k+1}^{M}\left(\dfrac{s_i-w_{i}}{s_{i}}\right)\\ =&\dfrac{w_k}{s_k}\cdot\prod_{i=k+1}^{M}\left(\dfrac{s_{i-1}}{s_{i}}\right)\\ =&\dfrac{w_k}{s_M}=\dfrac{w_k}{\sum_{i=1}^{M}w_i} \end{aligned} \]
Spatiotemporal reuse
- 每个像素我们只能保存 \(M\) 个样本,只用这 \(M\) 个样本限制了采样的质量
Initial candidates
- 从 \(M\) 个样本中 RIS 采样得到一个样本
Spatial reuse
- 一个像素周围的样本比较接近,可以复用
- 找到 spatial neighbors,然后继续 RIS
- spatial neighbors:picked randomly from a disk
- RIS 的过程可以多次进行,但是代价就是相关性会增加
- 样本的采样分布差别大,需要使用高级的 MIS(例如 generalized balance heuristic)
- Do not choose which spatial neighbors to reuse based on the random samples stored at these neighbors, as this causes bias!(这是为什么?)
Temporal reuse
- 相邻帧比较相似,可以复用
- 通过 motion vectors 重投影
- 也需要高级的 MIS
- access to previous frames’ target functions is required to remove all bias.
例子:ReSTIR DI
- ReSTIR for direct illumination
- 直接光照:3 个顶点的路径(只反弹一次)
- 相机 \(\to\) 光源:\(\bar{x}=[\mathrm{x}_0,\mathrm{x}_1,\mathrm{x}_2]\)
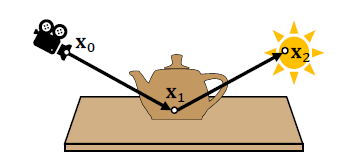
- \(x_2\in A\),\(A\):光源表面的点的集合
- 选定 \(\mathrm{x}_0,\mathrm{x}_1\),任务转化为如下
\[ L(\mathrm{x}_1\to \mathrm{x}_0)=\int_Af_s(\mathrm{x}_2\to \mathrm{x}_1\to \mathrm{x}_0)G(\mathrm{x}_1\leftrightarrow \mathrm{x}_2)V(\mathrm{x}_1\leftrightarrow \mathrm{x}_2)L_e(\mathrm{x}_2\to \mathrm{x}_1)\;\mathrm{d}\mathrm{x}_2 \]
- 反正就是一个 \(\mathrm{x}_2\)
的函数
- pixel dependent \(f_i\):像素变了,\(\mathrm{x}_1,\mathrm{x}_2\) 就会变了
\[ L(x_1\to x_0)=\int_Af(\mathrm{x}_2)\;\mathrm{d}\mathrm{x}_2 \]
- ReSTIR:不同像素间共享 \(\mathrm{x}_2\)
- we resample \(\mathrm{x}_2\) from one or more independent canonical samples covering the current pixel(保证无偏), plus samples borrowed from other pixels and frames(复用).
Target function
- \(x\) 代替 \(\mathrm{x}_2\),\(f\) 如下
\[ f(x)=f_{s}(x)G(x)V(x)L_{e}(x) \]
- target \(\hat{p}=f\)
\[ \hat{p}(x)=f_{s}(x)G(x)V(x)L_{e}(x) \]
- 早期论文近似:去掉 \(V\) 项,方便计算,但是需要特殊处理保证正确性
\[ \hat{p}(x)=f_{s}(x)G(x)L_{e}(x) \]
Initial candidates
- 为每个像素生成 canonical samples
- 对于 DI,可以在光源表面采样 \(M\) 个点,然后 RIS
- 复用的时候,使用 generalized balance heuristic MIS weight
- \(i\):第 \(i\) 个像素
\[ m_i(x)=\frac{\hat{p}_i(x)}{\sum_{j=1}^M\hat{p}_j(x)} \]
Spatial reuse
- 找到相似的像素,复用它的样本
- 启发式:GBuffer 中观察相似性
- 不能基于样本本身,bias
- 启发式:GBuffer 中观察相似性
- MIS 权重:\(1/M\) 会导致 bias
- 解决方案 sec7:contribution MIS weights
- 或者 generalized balance heuristic?
Temporal reuse
- motion vector 找到上一帧的样本,复用
- 计算 mis 需要使用到上一帧的 \(\hat{p}\),因此需要求可见性(需要保留上一帧的加速结构)
History length
- 如果时间复用,上一帧和现在赋相同的权重,那么会丢失 ~50% 的历史信息
- 引入 confidence weights \(c_j\)
\[ m_i(x)=\frac{c_i\hat{p}_i(x)}{\sum_{j=1}^Mc_j\hat{p}_j(x)} \]
- 越信任这个样本,\(c_i\) 越高
- effective sample count:corresponding to \(N\) samples
- 很难,因为 RIS 的样本来自不同分布,有效的数量难计算
- 可以简单的使用这个样本集成的样本数来表示(直接加起来)
- 相当于给出了一个上界
- 更有效的估计很难
- 实际上会将这个值 cap 到 <5~30(20 是个不错的选择)
- 否则会导致 \(c_i\) 指数增长,导致新样本权重太小了
- 算法如下

- 新样本:\(c_i=1\)
- 新进入屏幕的像素(没有 temporal precedessor),\(M=0\)
- 检测到 occlusions or disocclusions,\(M=0\)
- reset \(M=0\) 通过检测 GBuffer
- 不能基于样本本身,bias
Advanced topics
- light sampler 对于 glossy 的不友好
- BSDF lobe 小
- Improved light sampling
- 光源采样的时候:power-based importance sampling
- power:total emitted flux over the surface
- power 采光源,面积均匀采点
- “light tiles”(sec7)
- 不考虑着色点信息
- 光源采样的时候:power-based importance sampling
- Mixing BSDF and light sampling
- initial candidate:容易实现,常规 MIS
- 恰当地处理:shift mappings(sec5)
- RIS and domains
- 物体移动的话,采样空间变了;原始 RIS 不能处理
- shift mappings(sec5)
05-Reusing Between Domains
- Simply reusing vertices without modification does not allow reuse
through mirrors or glass.
- 反射定律会被违反
- shift mappings
Preliminaries
- 不同的 domains 之间的样本复用
- 例如 path spaces seen by different pixels
Shift mappings
- shift mapping:最早是在 Gradient-Domain MLT 中提出,用于像素间的复用
- 路径变换 \(A\to B\),\(y=T(x)\)
- reconnection shift
- \(\mathrm{x}_2\) 之后的路径不变,开头直接和 \(\mathrm{x}_2\) 相连
- diffuse and rough surfaces 效果不错,但是 glossy or specular surfaces 不行(连接的光路不成立)
\[ T_{i\to j}([{\color{red}\mathrm{x}_{i,0},\mathrm{x}_{i,1}},\mathrm{x}_{2},\mathrm{x}_{3},\cdots]) =[{\color{red}\mathrm{x}_{j,0},\mathrm{x}_{j,1}},\mathrm{x}_{2},\mathrm{x}_{3},\cdots] \]
其他:half-vector shift、random replay shift
定义:Lin et al. (2022)
子集的双射
a shift mapping \(T\) from \(A\) to \(B\) is a bijective function from a subset \(\mathcal{D}(T)\subset A\) to its image \(\mathcal{F}(T)\subset B\)
undefined shifts 也要满足双射:如果 \(x\) 不能被 \(T\) 变换成 \(y\),那么不能存在 \(y\) 能逆变换回 \(x\)
实现上,在 \(T_{i\to j}\) 的过程中可能会设置 停止条件,返回 undefined
Jacobian determinants
- 多变量的话称作 Jacobian matrix
- pdf 的变化
- \(W_Y=\dfrac{1}{p_Y(Y)}\)
- \(Y=T(X)\) 则有
\[ p_Y(Y)=\frac{p_X(X)}{\vert T'(X)\vert},\quad W_Y={\vert T'(X)\vert}W_X \]
Reusing samples between domains
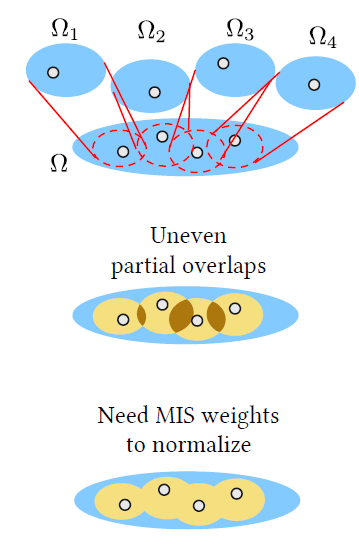
- 和原来的区别,采样的时候可以在 \(\Omega_i\) 上进行,复用的时候变换到 target
domain \(\Omega\)
- shift failed:\(w_i=0\)
- \(W_{X_i}\):定义在 \(\Omega_i\) 上的
- \(W_{Y_i}={\vert T_i'(X_i)\vert}W_{X_i}\)

- 为了保证覆盖整个 \(\Omega\):加入
canonical sample,使用 \(\hat{p}\)
采样(\(\Omega_i=\Omega\))
- \(T_i(x)=x,\vert{T_i'(x)}\vert=1\)
- 算法流程

MIS between domains
- 如果我们知道 \(X_i\) 生成的 \(\Omega_i\) 上的 pdf
- \(y\in\Omega\),\(p_{Y_i}\) 是 \(p_i\) 映射到 \(\Omega\) 上的 pdf
\[ m_{i}(y)=\frac{p_{Y_{i}}(y)}{\sum_{j=1}^{M}p_{Y_{j}}(y)} \]
- 根据
- \(y=T(x)\)
- 变换规则:\(p_Y(y)=\dfrac{p_X(x)}{\vert T'(x)\vert}\)
- 双射
\[ p_{Y_i}(y)=p_{X_i}\left(T_i^{-1}(y)\right) \left|T_i^{-1'}(y)\right| \]
- 无法映射,则 \(p_{Y_i}(y)=0\)
- 这一点允许我们使用 \(\hat{p}\) 作为代理(不需要特殊计算值)
- 相当于都转化到 \(\Omega\) 上,然后使用 generalized balance heuristic
\[ \hat{p}_{\leftarrow i}(y)= \left\{ \begin{array}{ll}\hat{p}_i\left(T_i^{-1}(y)\right)\left|T_i^{-1\prime}(y)\right|,&\text{if}\;y\in T_i(\text{supp}\;X_i)\\ 0&\text{otherwise} \end{array} \right. \]
- generalized balance heuristic
\[ m_i(y)=\frac{\hat{p}_{\leftarrow i}(y)}{\sum_{j=1}^M\hat{p}_{\leftarrow j}(y)} \]
- weighted 版本
\[ m_i(y)=\frac{c_i\hat{p}_{\leftarrow i}(y)}{\sum_{j=1}^Mc_j\hat{p}_{\leftarrow j}(y)} \]
- 要求
\[ \mathop{\sum_{i=1}^M}_{y\in T_i(\operatorname{supp}X_i)}m_i(y)=1 \]
- 这样 MIS 的计算量还是太大了:\(O(M^2)\)
- 之后有优化( sec7)