Deep Reinforcement Learning Course(4)
Unit4
- Policy Gradient With Pytorch
Introduction
- 直接优化 policy
- policy gradient 是其中一类方法
- Monte Carlo Reinforce 是一种 policy gradient 方法
policy-based methods
- What are the policy-based methods?
- 3 类强化学习方法
- value-based methods
- policy-based methods
- actor-critic method:上面两种的结合
- policy based:参数化 policy
- 例如使用 NN 输出一个行动上的分布:\(\pi_\theta(s)=\mathbb{P}[A|s;\theta]\),然后使用梯度下降优化参数
- 流程:CartPole-v1 游戏为例
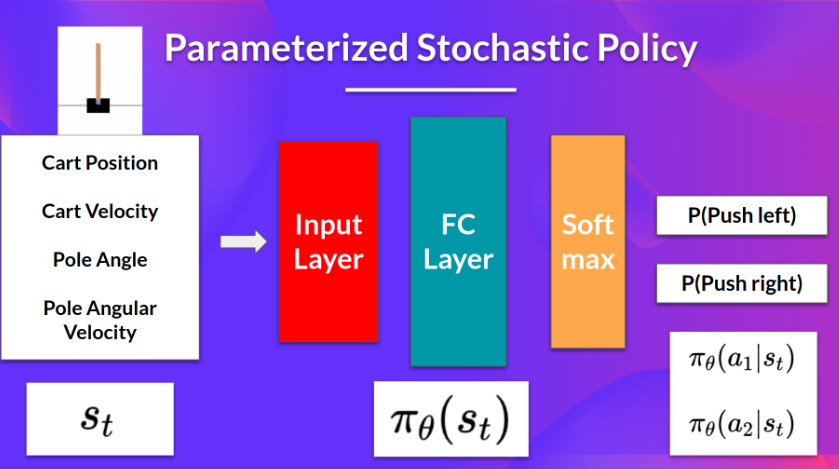
- policy-based methods 和 policy-gradient methods 的区别
- policy-gradient 是一种 policy-based 方法
policy-gradient 的优缺点
Advantages
- 可以直接输出 policy(不需要保存额外的 action 数据等)
- 不需要自己实现 exploration/exploitation trade-off
- 可以学习随机策略
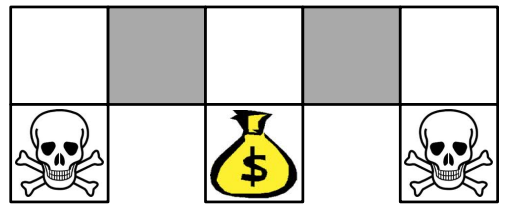
不需要处理 perceptual aliasing 问题:相同/类似状态,但是需要不同的行动
如下任务:机器人寻宝游戏;机器人只能感知到前后左右的墙壁状态
灰色区域状态相同,都是 \(\phi(s)=\overbrace{(\underbrace{1}_{\text{up}}\underbrace{0}_{\text{right}}\underbrace{1}_{\text{down}}\underbrace{0}_{\text{left}})}^{\text{walls=state}}\)
如果输出结果一样(往左或往右),此时很难找到财富(只能靠 exploration)
随机策略(往左、往右各50%)则会好很多
- 高维、连续行动空间效果更好
- Deep Q-Learning 无法处理无穷种行动的情况
- 例如自动驾驶,转方向盘的角度有无穷种可能
- 收敛性更好
- 随机策略的 policy 随着训练变化慢
- 如果是确定性策略,例如上一时刻 Q-value \(\text{(l,r)=(0.10,0.09)}\),然后这一时刻变成了 Q-value \(\text{(l,r)=(0.10,0.11)}\),那么 policy 就发生了剧变
Disadvantages
- 容易陷入局部最优
- 训练更慢
- 方差大
深入 policy-gradient methods
- parameterized stochastic policy
- action preference:the probability of taking each action
- 目标:更多的采样收益更大的行动
- idea:如果当前 episode 收益高,则认为当前 episode 中所有的 action 都是好的
- Training Loop 的伪代码如下
- Collect an episode with the \(\pi\) (policy).
- Calculate the return(sum of rewards).
- Update the weights of the \(\pi\)
- If positive return \(\to\) increase the probability of each (state, action) pairs taken during the episode.
- If negative return \(\to\) decrease the probability of each (state, action) taken during the episode.
- score/objective function(目标函数):\(J(\theta)=\mathbb{E}_{\tau\sim\pi}[R(\tau)]\)
- 和 episode 不同,trajectory 只有一系列 state、action,不包括 reward
- \(J(\theta)\):输入 trajectory,输出期望 return
- expected return:expected cumulative reward
- 理解:感觉像是压缩了信息,直接把 reward 信息保存到 \(\theta\) 里面了
\[ J(\theta)=\sum_\tau P(\tau;\theta)R(\tau) \]
\[ P(\tau;\theta)=\left[\prod_{t=0}P(s_{t+1}|s_t,a_t)\pi_\theta(a_t|s_t)\right] \]
- 目的:找到 \(\theta\),最大化目标函数
Gradient Ascent
- 最大化 \(\to\) gradient ascent(梯度上升)
- 梯度上升:\(\theta\leftarrow\theta+\alpha*\nabla_\theta J(\theta)\)
- 问题
- 无法准确计算梯度,通过样本进行估计
- 不能对状态微分(Markov Decision Process dynamics)
- 如何微分?Policy Gradient Theorem!
- 对任意可微的 policy、任意目标函数,都有
- 红色部分应该加上吧?
- 对任意可微的 policy、任意目标函数,都有
\[ \nabla_\theta J(\theta)=\mathbb{E}_{\pi_\theta}\left[{\color{red}\sum_{t=0}}\nabla_\theta\log\pi_\theta(a_t\mid s_t)R(\tau)\right] \]
Reinforce algorithm
- Monte Carlo Reinforce、Monte-Carlo policy-gradient
- 算法流程(Loop)
- Use the policy \(\pi_\theta\) to collect an episode \(\tau\)
- Use the episode to estimate the gradient \(\hat{g}=\nabla_\theta J(\theta)\)
- \(\nabla_\theta J(\theta)\approx\hat{g}=\sum_{t=0}\nabla_\theta\log\pi_\theta(a_t|s_t)R(\tau)\)
- Update the weights of the policy:\(\theta\leftarrow\theta+\alpha\hat{g}\)
- collect multiple episodes (trajectories):梯度多次平均
\[ \nabla_\theta J(\theta)\approx\hat{g}=\frac1m\sum_{i=1}^m\sum_{t=0}\nabla_\theta\log\pi_\theta(a_t^{(i)}|s_t^{(i)})R(\tau^{(i)}) \]
the Policy Gradient Theorem
- derivative log trick(also called likelihood ratio trick or REINFORCE trick)
\[ \begin{aligned} \nabla_\theta J(\theta) &=\nabla_\theta\sum_\tau P(\tau;\theta)R(\tau)\\ &=\sum_\tau \nabla_\theta P(\tau;\theta)R(\tau)\\ &=\sum_\tau \frac{P(\tau;\theta)}{P(\tau;\theta)}\cdot \nabla_\theta P(\tau;\theta)R(\tau)\\ &=\sum_\tau \frac{P(\tau;\theta)}{P(\tau;\theta)}\cdot \nabla_\theta P(\tau;\theta)R(\tau)\\ &=\sum_\tau P(\tau;\theta)\nabla_\theta \log P(\tau;\theta)R(\tau)\\ \end{aligned} \]
- 展开 \(P\)
- initial state distribution \(\mu(s_0)\),state transition dynamics \(P\)
- 二者都不依赖于 \(\theta\)
- initial state distribution \(\mu(s_0)\),state transition dynamics \(P\)
\[ \begin{aligned} \nabla_\theta \log P(\tau;\theta) &=\nabla_\theta \log\left[\mu(s_0)\prod_{t=0}^HP(s_{t+1}\mid s_t,a_t)\pi_\theta(a_t\mid s_t)\right]\\ &=\nabla_\theta\left[\log\mu(s_0)+\sum\limits_{t=0}^H\log P(s_{t+1}\mid s_t,a_t)+\sum\limits_{t=0}^H\log\pi_\theta(a_t\mid s_t)\right]\\ &=\nabla_\theta \log\mu(s_0)+\nabla_\theta\sum_{t=0}^H\log P(s_{t+1}\mid s_t,a_t)+\nabla_{\theta}\sum_{t=0}^{H}\log\pi_{\theta}(a_{t}\mid s_{t})\\ &=\nabla_{\theta}\sum_{t=0}^{H}\log\pi_{\theta}(a_{t}\mid s_{t}) \end{aligned} \]
- 于是
\[ \begin{aligned} \nabla_\theta J(\theta) &=\sum_\tau P(\tau;\theta)\left[\nabla_{\theta}\sum_{t=0}^{H}\log\pi_{\theta}(a_{t}\mid s_{t})\right]R(\tau)\\ &=\sum_\tau\sum_{t=0}^{H} P(\tau;\theta)\nabla_{\theta}\log\pi_{\theta}(a_{t}\mid s_{t})R(\tau) \end{aligned} \]
HW4
不倒木棒
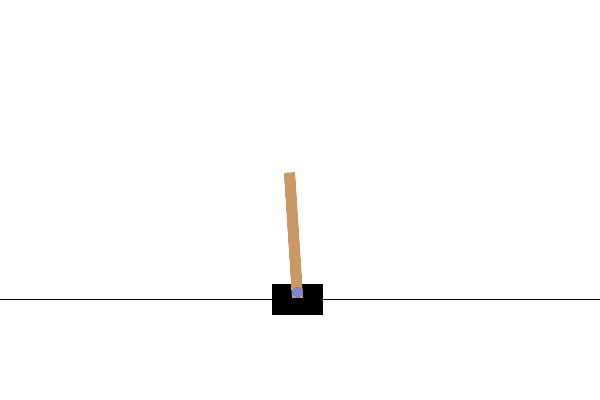
- CartPole-v1
- 观察空间:4(Cart 位置、速度;Pole 角度、角速度)
- 行动空间:2(左右)
- 算法:Allgorith REINFORCE
\[ \begin{aligned} &\text{1: }\textbf{procedure}~\text{REINFORCE}\\ &\text{2: }\quad\text{Start with policy model}~\pi_\theta\\ &\text{3: }\quad \textbf{repeat}:\\ &\text{4: }\quad \quad\text{Generate an episode}~S_0,A_0,r_0,\ldots,S_{T-1},A_{T-1},r_{T-1}\text{ following } \pi_\theta(\cdot)\\ &\text{5: }\quad \quad \textbf{for}~t~\text{from}~T-1~\text{to}~0:\\ &\text{6: }\quad \quad \quad G_t=\sum_{k=t}^{T-1}\gamma^{k-t}r_k\\ &\text{7: }\quad \quad L(\theta)=\frac1T\sum_{t=0}^{T-1}G_t\log\pi_\theta(A_t|S_t)\\ &\text{8: }\quad \quad \text{Optimize}~\pi_\theta~\text{using}~\nabla L(\theta)\\ &\text{9: }\textbf{end procedure}\end{aligned} \]
Flappy Bird
![]()
- PixelCopter
- 观察空间:7(y 坐标、速度、到地板、天花板的距离、下一个障碍物水平 x 距离、下一个障碍物的左上角、右下角的 y 坐标)
- 行动空间:2(上升、不动)