(论文)[2022-SIG] EARS: Efficiency-Aware Russian Roulette and Splitting(2)

Posted on Edited on Views:
RRS 实现部分

EARS

Efficiency-Aware RRS

Application to rendering

  • 两个问题
    • 每一个像素都是一个积分
    • RRS 发生在很多跳上

Objective

  • 找到一个最优的 local splitting factors 使得整张图片的 total efficiency 最大化
    • 仍然是一个凸优化问题（凸函数的和）
  • relMSE 取代 MSE
    • 方差部分，如果使用原始目标函数的绝对误差度量，会导致一直在优化比较亮的像素，我们使用如下的相对误差度量
    • MSE：对亮区域过度采样，导致计算开销都花在比较亮的区域上
    • relMSE：计算开销分布更加平均

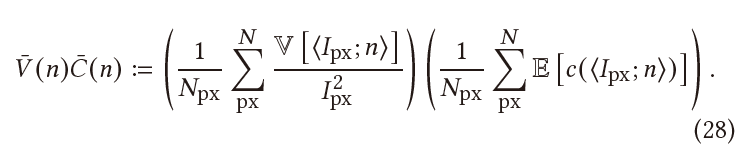
  • 问题：\(I_{\text{px}}\) 不可知（使用降噪后的结果作为标准值）

不动点迭代函数

  • 第 \(i\) 次迭代

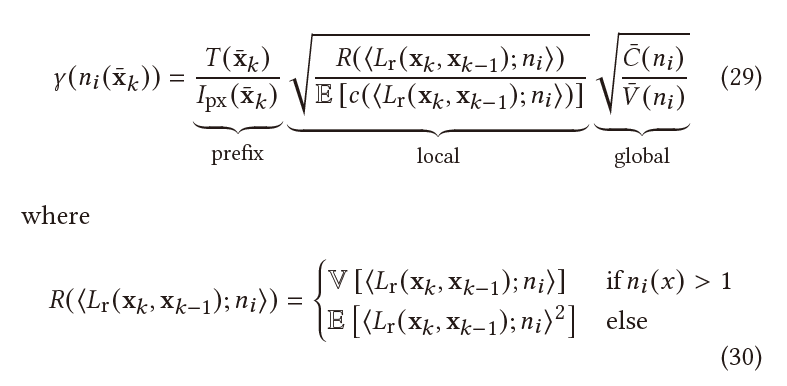
  • 计算过程和之前类似

\[ \dfrac{\partial{\bar{V}(n)\bar{C}(n)}}{\partial{n}}=\dfrac{\partial{\bar{V}(n)}}{\partial{n}}\bar{C}(n)+\bar{V}(n)\dfrac{\partial{\bar{C}(n)}}{\partial{n}}=0 \]

  • 细节
    • \(I_{\text{px}}\) 来自于 relMSE
    • \(T(\bar{\mathrm{x}}_k)\) 是从 \(R\) 项中提取出来的，也就是之前等式 18、23 中的 \(\dfrac{g}{p}\) 项
  • 3个部分
    • prefix：已知
    • local：局部估计，可以存储在 5D 的数据结构里
    • global：全局信息，可知（所有像素的平均计算代价、方差 \(\sum_{\text{px}}\) ）
  • 算法优势
    • 虽然是不动点迭代的算法，不需要为所有的前缀路径 \(x\) 显式存储连续的 RRS 函数 \(n(x)\)
    • 我们只存储相关的统计量（方差、开销）用于下一轮的迭代
      • 不是每到一个点就迭代计算 n(x) 吗？对的，不是
    • 每次迭代随机更新一组前缀 \(x\)
      • 只要前缀能够被采样到，那么更新概率就不为 0，因此最终能收敛
    • 1997 年的论文依赖于前缀 \(x\) 的长度，因此需要降维才能计算，该方法不依赖

收敛性

  • \(\bar{\mathrm{x}}\) 前后的点是否发生 RRS，不影响这个点 RRS 的收敛性
  • 其他的点和 \(\bar{\mathrm{x}}\) 处的 RRS 的收敛无关
    • 不影响附录 C 收敛性的证明

例子

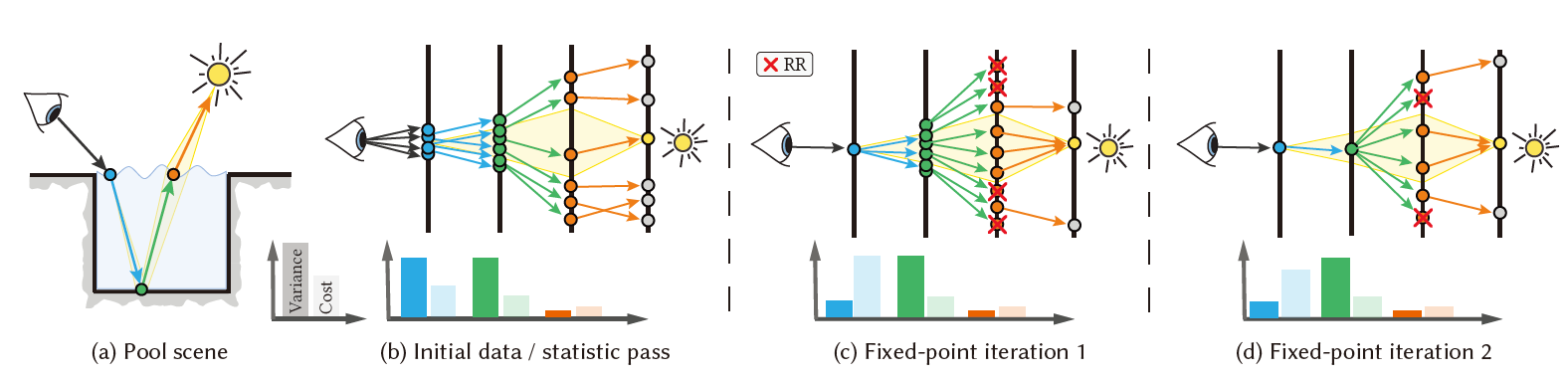
    1. 场景设置，黄色部分表示能够产生的焦散的地方
    1. 初始化，classic albedo-based RR（没有 S）（具体看代码），同时保存每一个点的 \(\langle L_i\rangle\) 的统计量（方差、开销）
    • 方差：反向传播（主要在 diffuse 表面）
    • 开销：初始开销 = 后缀长度
    1. 第一次迭代，高方差 S 分裂（蓝色、绿色节点），找不到光源的（黄色区域外）被 RR 删除（橙色节点）
    1. 第二次迭代，高方差分裂（绿色节点），找不到光源的被 RR 删除（橙色节点）

实现

  • Mitsuba 0.6，递归 PT 为基础
  • iterative rendering process
    • 每一轮迭代，对每一个像素采样样本，用于计算 global/local 的方差
    • local 的估计存储在 5D 数据结构中
  • 算法：
    • 初始：classic prefix weight-based RR
    • 迭代：根据 式子29 更新 RRS 值
  • 减小计算开销：慢慢增长迭代的时间（多 spp 更新），从而减少更新次数
  • 迭代早期图片方差大，方差倒数加权合并
    • 最优合并问题（the optimal combination of image）
    • 引入 bias（方差估计使用的样本问题）
      • bias 小，可忽视，随着迭代增加消失
      • TODO：David Kirk and James Arvo. 1991. Unbiased Sampling Techniques for Image Synthesis
  • 算法伪代码

  • LrEstimate 中的 contribution 部分应该除以样本数（splitting factor）

Adapting the theory

NEE

  • 和 ADDR 一样，把 NEE 和 BSDF 采样作为一个原子操作（1 NEE + 1 BSDF）
  • 这样设定下，RRS 的分析和之前一致，仍然最优
  • 更一般情况下则不是最优（NEE 数量和 BSDF 数量在不同的 shading point 不一样）

Handling colors

  • 多通道
  • 方差对所有通道平均

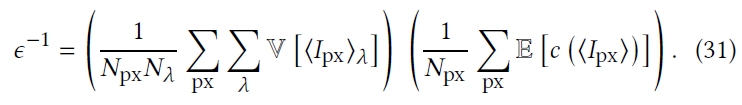
  • 此时最优化的区别就是，需要在对 \(\lambda\) 求平均
    • component-wise
    • \(I_{\text{px}}\) 表示 relMSE，上面 \((31)\) 没有显式写

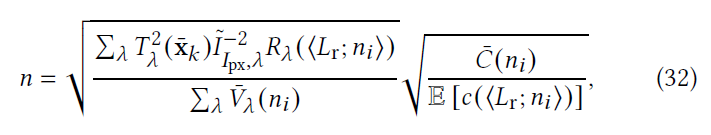
Cost heuristic

  • 光线数量
  • 简单近似：所有光线计算代价相同
    • shadow rays
    • primary rays from the camera
    • BSDF samples

Clamping

  • RRS：\((0.05,20)\)
  • 可以避免
    • bias：\(n(x)=0\)
    • 过多的光线，RRS 过大

Global estimates

  • 全局的计算开销
    • 对所有像素求平均
    • 一个迭代轮可能有多个 spp

  • relMSE：和降噪后的图片 \(\tilde{I}_{\text{px}}\) 做对比
    • \(\langle{I_{\text{px}};n}\rangle_{s}\) 包括 splitting，每一个 path tree 都会被考虑

  • outlier：去除 \(0.001\%\) 方差最大的样本

Local Estimate

  • 空间八叉树 octree + 方向树 histogram
  • 方向：\(4\times4\) 直方图，高分辨率提升不大
  • octree，40000+样本时候分裂叶子节点（类似 PPG）

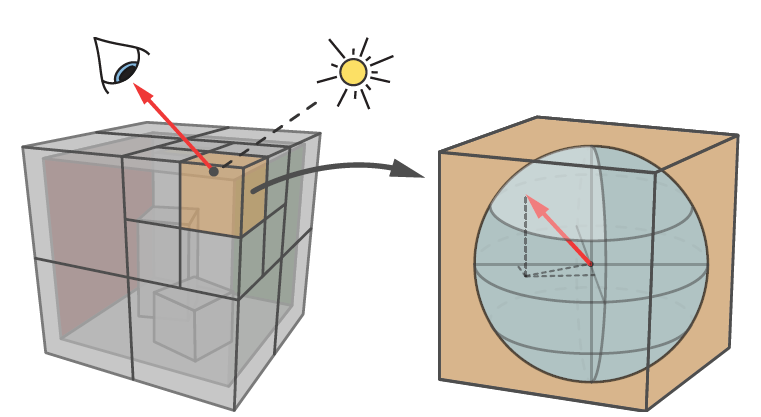
Building the estimates

  • 每一个方向 \(b\) 保存统计量
    • 方差：\(\tilde{V}_b\)
    • 二阶矩：\(\tilde{M}_b\)
    • \(\langle{L_\text{r}}\rangle\) 的计算开销：\(\tilde{C}_b\)
  • \(n_b\)：\(b\) 内的样本数
  • 二阶矩

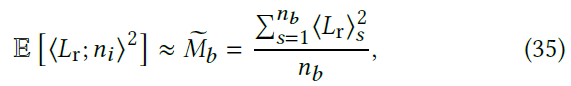
  • 方差
    • 这里做了近似
      • TODO：近似是什么？
    • \((37)\) 应该没有平方

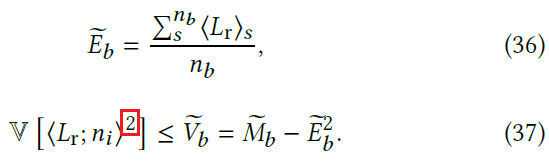
Incremental learning

  • 根据不动点的理论，这一轮统计量的更新应该只依赖于上一轮，但是如此收敛慢，因此将之前所有轮次的统计量都使用
  • 利用之前的样本进行学习
    • 收敛率有所降低，但是统计量可靠性提升了，最终变快了

EVALUATION

  • 和 ADRRS 进行对比
  • 对比场景
    • 只有 RR
    • RR+S
    • 只有 S（都表现得不好）
  • baseline
    • classic prefix weight-based RR（5th bounce 开始启用）
    • adaptive sampling variant（在线学习方差，预先提供了GT，但是不算在渲染时间中）
  • 测试
    • equal-time（10min）
    • AMD Ryzen 3950X CPU with 16 cores
    • max depth：40
  • 结果 relMSE（平均）
    • \(1.52\times\) ADDR
    • \(5.87\times\) classic RR
  • 最差（Glossy Bathroom）比 ADDR 慢 \(9\%\)
  • 场景介绍
    • Modern Living Room
      • mostly diffuse，large spherical light（前向 PT 友好）
      • 结果
        • 与 ADRRS 相比，没有明显提升，但是噪声更均匀
        • 与 Adaptive PT 相似，焦散噪声变小，其他地方轻微变大
        • 简单场景中，不如简单算法效果好（额外开销大）
    • Bookshelf、Living Room
      • strong，difficult diffuse indirect illumination
      • 结果
        • 暗表面过多，classic RR 提前停止
        • Splitting 相较于 Adaptive 的优势，一旦找到一条可行光路，能够生成若干其他可行光路
    • Pool
      • 优于 ADRRS（variance and cost > expected contributions）
    • Kitchen（上面两类场景的并集）
    • Glossy Bathroom
      • homogeneous illumination
      • 过于简单了

统计数据

  • 考虑 RR，spp 数增加
  • 考虑 S，spp 数减小
  • 和 ADRRS （up 2）相比，EARS 一条光线的分裂数更多（up 67）
    • 而且更多发生在光线和场景的第一个交点（ADRRS：1，EARS：up 18）
  • 哪里方差大就去优化哪里

overhead

  • 5D tree：24M，空间划分：22,000 regions
    • 再大之后，计算开销比收益更大

Convergence

  • 理论收敛，但是实际有问题
  • 原因：noise in the estimates
  • 测试：充足迭代轮，能够收敛

Path Guiding

  • 和 Muller 的 PPG 结合
    • 数据结构一样
  • classic RR：throughout weight
    • albedo 的乘积效果更好
    • 暗表面的 guiding，如果某个方向采样 pdf 大，但是 throughout weight 低，则 RR 可能会删除（好处抵消了）

limitation and future work

  • limit：the accuracy of the required estimates
  • future：EARS 和 image space adaptive sampling and bidirectional algorithms 结合

Estimation error

  • Noise in the local estimates
  • 不同 cache 的样本数相差太大，估计的准确率相差太大：收敛速度不一样

  • 解决方案：spatial filtering（sharing estimates between caches）

Combining with Adaptive Sampling

  • 在 primary hit point 就是使用了 RR（增大了方差，把计算资源分配给其他像素了，总体效率提高）
    • local 方差小，global 方差大
    • 可以直接和 adaptive 相结合，直接不采样这些光线（本身也是浪费了），效率更高
  • 改动：maximize the efficiency of each individual pixel

Bidirectional methods

  • BDPT 需要考虑 MIS 权重，RRS 也会成为其中的一部分，更加复杂了
  • 视子路 RRS 会影响 光子路 RRS，更难优化（非凸问题）
  • 相关性问题

其他

  • Participating media
  • Correlated sampling
    • uncorrelated sampling：方差 \(\propto O(n^{-1})\)
    • QMC 并不是
    • quasi-Monte Carlo sampling
  • Dynamic scenes
    • 学习得到的统计量在帧间复用

收敛性证明

  • 凸函数就能保证
  • 如下证明以 S 为例
  • \(\gamma(n)\) 函数：等式 29
    • 恒正
    • 只有 global 部分相关

\[ \gamma(n)=A\sqrt{\dfrac{a+bn}{c+\dfrac{d}{n}}}\in O(\sqrt{n}) \]

  • 于是有

\[ \gamma'(n)>0,\gamma'(n)\in O\left(\dfrac{1}{\sqrt{n}}\right) \]

  • 于是 \(\gamma(n)\) 是严格递增的凹函数，而且具有如下的极限性质

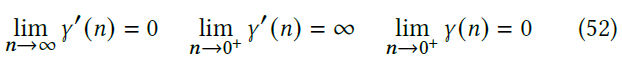
  • 大致图形如下

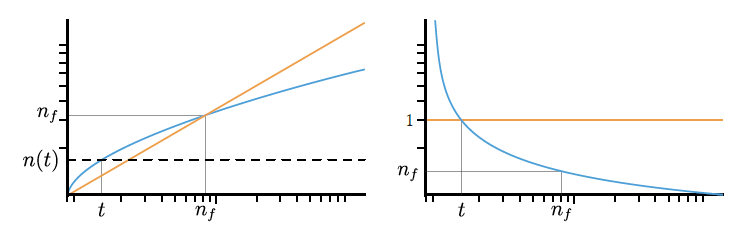
  • 此时，存在 \(t\) 满足 \(\gamma'(t)=1,\gamma(n_f)=n_f\)
    • \(x>t\)：满足条件
      • \(\gamma'(x)<1\)
      • 自映射：\([n(t),\infty)\subset [t,\infty)\)
    • \(x<t\Rightarrow \gamma(x)>x\)
  • RR、RRS 证明同理

总结

  • 不动点迭代的体现
    • 使用上一轮的统计量更新 RRS，使用这一轮的 RRS 更新统计量
    • 下一轮使用的统计量相当于是使用这一轮更新得到的
    • 统计量的迭代更新和 RRS 的迭代更新是一致的
  • 不动点迭代逻辑：\(\gamma_{i-1}\to\text{local}_{i-1}\to\gamma_{i}\)