(论文)[2023] 基于子空间的双向路径连接渲染技术(3)

Posted on 2023-07-25 Edited on 2023-08-03 Views:

BDPT，代理追踪技术，倒数的无偏估计方法（泰勒展开、类路径追踪方法，RRS 方法）

基于子空间的双向路径连接渲染技术(3)

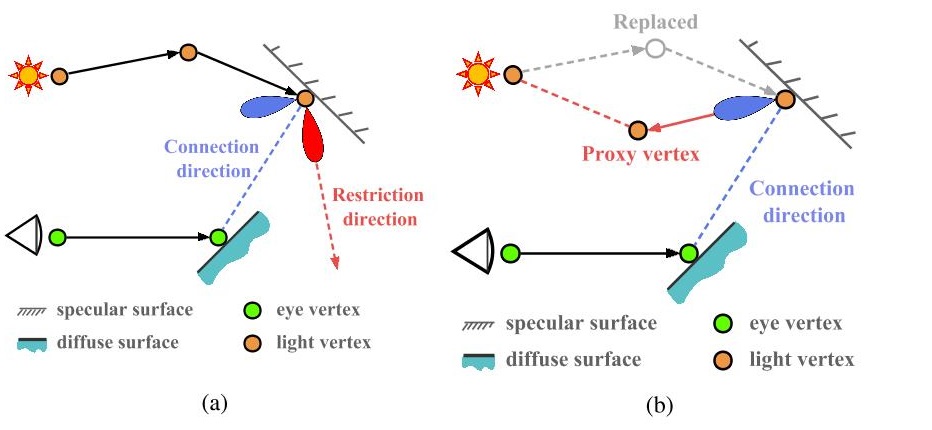
代理追踪技术

概率连接难以解决的问题：光滑材质的镜面投射光路
- 光子路末端顶点在光滑表面，视子路末端顶点在漫反射表面
- 视子路末端顶点落在光子路末端反射的 BSDF 波瓣（狭长）中概率低
代理追踪：调整差的路径顶点

子路径追踪分析

采样路径就是采样路径点

\[ p(\bar{x})=\prod_{i=0}^{k-1}p(x_i) \]

子路径

\[ p(x_i)=p(x_{i-1}\to x_i) \]

路径连接：\(\bar{x}=\bar{y}\bar{z}\)（光子路+视子路）

\[ p(\bar{x})= \left(p(y_0)\prod_{i=1}^{s-1}p(y_{i-1}\to y_{i})\right) \left(\prod_{i=1}^{t-1}p(z_{i}\leftarrow z_{i-1})p(z_0)\right) \]

对于光滑表面 \(y_{s-1}\)，漫反射表面 \(z_{t-1}\)，一个优秀的连接要求
- \(B(y_{s-2}\to y_{s-1}\to z_{t-1})\) 值高
问题：
- 连接策略：概率连接没有考虑这个分量
  - 其采样概率如果包含这个分量，则效果与其更加匹配
- 直接从漫反射表面 \(z_{t-1}\) 进行追踪，很难达到高 BSDF 贡献的要求

代理采样

得到的光路的某些顶点分布差，有些顶点分布好，希望能够保持其他顶点不动的情况下，修改差的顶点的分布
- 重新采样我们指定的部分顶点
算法流程如下
- 常规路径追踪得到完整路径 \(\bar{x}_0=x_0x_1\cdots x_{s-2}x_{s-1}\)
- \(\bar{x}_0\) 划分为：固定顶点组成的残缺路径 \(\bar{h}\) + 可替换顶点组成的路径 \(\bar{g}\)
  - 删除操作：\(\bar{h}=D(\bar{x}_0,\bar{g}_0)\)
- 根据 \(\bar{h}\) 生成一个代理路径 \(\bar{g}\)，并将 \(\bar{g}\) 添加到残缺路径 \(\bar{h}\) 中
  - 修补操作：\(\bar{x}=R(\bar{h},\bar{g})\)

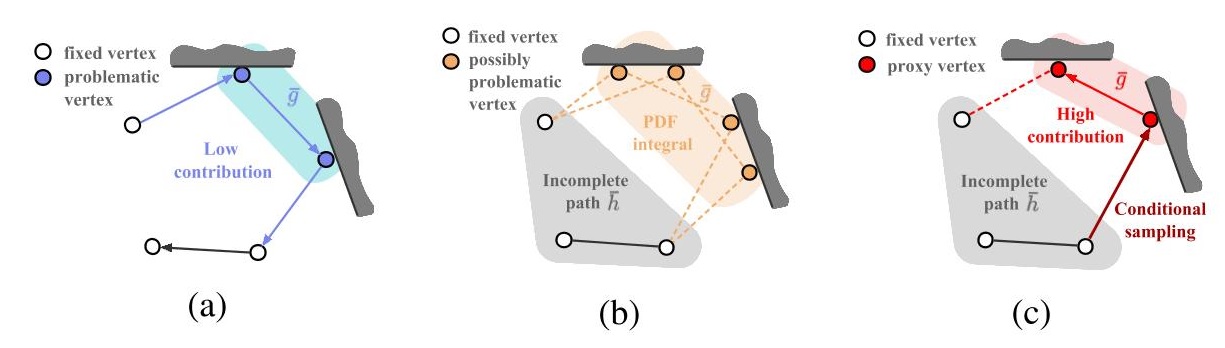
最终采样概率
- 注意这里的 \(p_1(\bar{h})\ne p(\bar{x}_0)\) ，因为可能有多个 \(\bar{x}_0\) 可以生成 \(\bar{h}\)（如上图 b）

\[ p_d(\bar{x})=p_1(\bar{h})p_2(\bar{g}\mid\bar{h}) \]

\(p_1(\bar{h})\) 计算如下：对所有可能生成残缺路径 \(\bar{h}\) 的路径做积分

\[ p_1(\bar{h})=\int_{A^u}p\left[R(\bar{h},\bar{g})\right]\;\mathrm{d}\mu(\bar{g}) \]

代理采样优势：当 \(p_2(\bar{g}\vert\bar{h})\) 性能足够好的时候，优势明显
- 适合光滑顶点，因为出射 lobe 小
问题：倒数的无偏估计?
- MC 框架中，最终贡献 \(\dfrac{f(\bar{x})}{p_d(\bar{x})}\) ，但是分母中 \(p_1(\bar{h})\) 项难求
- 如果我们直接 MC 求解 \(p_1(\bar{h})\)，则最终结果也不是无偏的
  - 如下推理不一定成立

\[ E(X)=\mu\Longrightarrow E(\dfrac{1}{X})=\dfrac{1}{\mu} \]

倒数的无偏估计方法

问题定义

\(f(x):\mathcal{D}\to\mathbb{R}\)
采样分布 \(p(x)\) 满足 \(f(x)>0\Rightarrow p(x)>0\)
\(\int_{\mathcal{D}}f(x)\;\mathrm{d}x=\beta\)
当前可以无偏的估计 \(\beta\)，如何无偏估计 \(\alpha=\dfrac{1}{\beta}\)

泰勒展开

使用泰勒展开进行估计，任意常数 \(B\)

\[ A=B-\beta \]

泰勒展开，在 \(A=0\) 处展开（变量是 \(A\)，\(B\) 是常数）

\[ f(x)=f(x_0)+\sum_{n=1}^{\infty}\dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^{n} \]

\[ \alpha=\dfrac{1}{B-A}=\dfrac{1}{B}+\dfrac{A}{B^2}+\dfrac{A^2}{B^3}\cdots=\dfrac{1}{B}\sum_{n=0}^{\infty}\dfrac{A^n}{B^n} \]

积分形式
- \(\bar{x}\) 由 \(N\) 个来自 \(\mathcal{D}\) 的样本组成
  - \(\mathrm{d}\mu(x)=\mathrm{d}x_1\cdots\mathrm{d}x_{n}\)
- 分母 \(B\) 是常数
- 分子 \(A^n\) 的无偏估计：\(n\) 个独立的期望为 \(A\) 样本累乘
  - \(X,Y\) 独立 \(\Rightarrow\) \(E(XY)=E(X)E(Y)\)

\[ \begin{aligned} \alpha &=\dfrac{1}{B}\sum_{n=0}^{\infty}\dfrac{A^n}{B^n}\\ &=\dfrac{1}{B}+\dfrac{1}{B}\sum_{n=1}^{\infty}I_n\\ &=\dfrac{1}{B}+\dfrac{1}{B}\sum_{n=1}^{\infty}\int_{\mathcal{D}^n}\prod_{i=0}^{n-1}\dfrac{B-f(x_i)}{B}\;\mathrm{d}\mu(\bar{x})\\ \end{aligned} \]

估计 \(\dfrac{A^{n}}{B^{n}}\)：期望为 \(\dfrac{A}{B}\) 的 \(n\) 个随机变量累乘

类路径追踪方法

上面的方式和路径追踪算法的结构类似，可以使用类似路径追踪的方法解决
- 对所有长度的子空间求和
定义贡献值函数

\[ g(x) = \dfrac{B - f(x)}{B} \]

重写 \(\alpha\)，单独处理 \(\mathbb{R}^0\)

\[ \alpha=\dfrac{1}{B}+\int_{\Omega}G(\bar{x})\;\mathrm{d}\mu(\bar{x}) \]

这里的路径空间如下
- 路径：\(\bar{x}=x_{0}\cdots x_{k-1}\)
- 路径的微分单元：\(\mathrm{d}\mu(\bar{x})\)

\[ \Omega=\sum_{n=1}^{\infty}\mathbb{R}^{n} \]

此时：\(G(\bar{x})\)

\[ G(\bar{x}) = \dfrac{1}{B}\prod_{i=0}^{k-1} g(x_i) \]

单向路径追踪的方法
- 因为涉及到无穷，需要使用俄罗斯轮盘赌来保证无偏性
- 每一个路径点的采样分布都是 \(p(x)\)
- 不管相关性，则一次追踪得到的不同前缀都是样本点
一个路径 \(\bar{x}\) 被采样到的概率
- \(\bar{x}_{i}\)：\(\bar{x}\) 以 \(x_{i}\) 为末端节点的前缀 \(x_{0}x_{1}...x_{i}\)
- 最后的累乘是 \((1-r(\bar{x}_i))\) 还是 \(r(\bar{x}_i)\)，看的只是停止的概率是 \(1-r(\bar{x}_i)\) 还是 \(r(\bar{x}_i)\) ，本质上没有区别
  - 这里是 \(1-r(\bar{x}_i)\) 的概率停止

\[ P(\bar{x}) R(\bar{x})= \prod_{i=0}^{k-1} p(x_i) \times \prod_{i=0}^{k-1}(1-r(\bar{x}_{i})) \]

为什么单向 PT 只取一条路径结果也是正确的呢？
- 因为击中光源之后就停止了（相当于最后乘上了 \(r(\bar{x}_{k-1})=1\)）
- \(r(x_i)\) 是任意指定的
单个路径的 MC 评估

\[ \tilde{I}(\bar{x}) = \dfrac{G(\bar{x})}{ P(\bar{x})R(\bar{x})} \]

考虑无偏性

一次采样得到的所有路径前缀：\(k\) 个样本

\[ \tilde{I}=\sum_{i=0}^{k-1} \tilde{I}(\bar{x}_{i}) = \sum_{i=0}^{k-1}\dfrac{G(\bar{x}_{i})}{P(\bar{x}_{i})R(\bar{x}_i)} \]

问题：泰勒展开如果忽略高阶项过多，则误差很大，如何选取 \(B\)、RR 值很重要
- 收敛慢

方差分析

根据我们定义的 \(g(x)\)，最优采样 \(p(x)\propto g(x)\) ，高贡献反而低采样，很反直觉，直观上效率差

\[ g(x) = \dfrac{B - f(x)}{B}=1-\dfrac{f(x)}{B} \]

估计

\[ I(x)=\dfrac{g(x)}{p(x)}=\dfrac{B - f(x)}{Bp(x)} \]

其他选择：已知部分不需要估计，此时最优采样 \(p(x)\propto f(x)\)，高贡献则高采样

\[ I(x) = 1 - \dfrac{f(x)}{Bp(x)} \]

此时整体的 MC 评估器

\[ \tilde{I}(\bar{x}) =\dfrac{1}{B R(\bar{x})}\prod_{i=0}^{k-1}\left(1 - \dfrac{f(x_i)}{Bp(x_i)}\right) \]

无偏性

\[ \begin{aligned} E(\tilde{I}) &=\int_{\Omega}\tilde{I}(\bar{x})P({\bar{x}})R(\bar{x})\;\mathrm{d} \mu(\bar{x})\\ &=\sum_{k=1}^{\infty}\int_{\mathbb{R}^k}\tilde{I}(\bar{x})P({\bar{x}})R(\bar{x})\;\mathrm{d} \mu(\bar{x})\\ &=\sum_{k=1}^{\infty}\int_{\mathbb{R}^k}\dfrac{1}{B}\prod_{i=0}^{k-1}\left(\left(1-\dfrac{f(x_i)}{Bp(x_i)}\right)p(x_i)\right)\;\mathrm{d}\mu(\bar{x})\\ &=\sum_{k=1}^{\infty}\int_{\mathbb{R}^k}\frac{1}{B}\prod_{i=0}^{k-1}\left(p(x_i)-\dfrac{f(x_i)}{B}\right)\;\mathrm{d}\mu(\bar{x})\\ (独立性)&=\sum_{k=1}^{\infty}\dfrac{1}{B}\left(\int_{\mathbb{R}^k}\left(p(x)-\dfrac{f(x)}{B}\right)\;\mathrm{d}x\right)^{k}\\ &=\sum_{k=1}^{\infty}\dfrac{1}{B}\dfrac{A^k}{B^k}\\ &=\alpha-\dfrac{1}{B} \end{aligned} \]

算法

RRS：Russian Roulette and Splitting
不断使用 \(p(x)\) 进行采样，当才到新样本 \(x_i\)，则和之前的采样结果结合成为新路径
当采样到一条新路径的时候，就开始使用 RRS 策略
- 如果 \(r(\bar{x})\in(0,1]\)：则 \(1-r(\bar{x})\) 的概率结束采样，\(r(\bar{x})\) 的概率继续
- 如果 \(r(\bar{x})>1\)：则以 \(r(\bar{x})-\lfloor{r(\bar{x})}\rfloor\) 的概率分裂出 \(\lfloor{r(\bar{x})}\rfloor+1\) 次采样，否则分裂出 \(\lfloor{r(\bar{x})}\rfloor\) 次采样
  - 相同前缀，后继节点的多次独立采样
推荐配置
- 此时只有 RR，没有 Splitting

\[ r(\bar{x})=\left\vert{1-\dfrac{f(x_{k-1})}{Bq(x_{k-1})}}\right\vert \]

\[ B=\max\left(\dfrac{f(x)}{q(x)}\right) \]

好处

求下面这样一个式子的积分的期望

\[ \int\dfrac{f(\bar{x})}{\int p_d(\bar{x}\mid\bar{g})p(\bar{g})\;\mathrm{d}\bar{g}}\;\mathrm{d}\bar{x} \]

如果通过先估计分母在估计分子的方式，此时只有每一轮 \(\bar{g}\) 的样本数趋向无限，结果才是无偏
- 但是在实际操作中我们只会让 \(\bar{x}\) 的样本数趋向无限，\(\bar{g}\) 的样本数只会是有限值，此时结果存在误差
通过上面倒数评估的方式，能够将分母的积分化开，变成分子，和的误差会比倒数和的误差小
具体查看实验