(论文)[2023] 基于子空间的双向路径连接渲染技术(2)
基于子空间的双向路径连接渲染技术(2)
基于子空间的概率连接双向路径追踪
光选择函数及其最优形式
- 光选择函数:\(\gamma(\bar{y},\bar{z}):\mathcal{S}\times\mathcal{S}\to\mathbb{R}\)
- \(\bar{y}\vert\bar{z}\)
- LVCBPT:\(\gamma(\bar{y},\bar{z})\propto p(\bar{y})\)
- PCBPT:\(\gamma(\bar{y},\bar{z})\propto f(\bar{y}\bar{z})\)
- 最优形式(需要考虑 MIS)
\[ \gamma^{\ast}(\bar{y},\bar{z})\propto w_t(\bar{y},\bar{z})f(\bar{y}\bar{z}) \]

- 细化
\[ f_y(\bar{y}) =L_e(y_0,y_1)GV(y_0,y_1)\left[\prod_{i=1}^{s-2}\rho({y}_{i-1},{y}_i,{y}_{i+1})GV({y}_i,{y}_{i+1})\right] \]
\[ f_{yz}(\bar{y},\bar{z})=\rho({y}_{s-2},{y}_{s-1},{y}_{t-1})GV({y}_{s-1},{y}_{t-1})\rho({y}_{s-1},{y}_{t-1},{y}_{t-2}) \]
\[ f_z(\bar{y}) =W_e({z}_{0},{z}_z)GV(z_0,z_1)\left[\prod_{i=1}^{t-2}\rho({z}_{i+1},{z}_i,{z}_{i-1})GV({z}_{i+1},{z}_{i})\right] \]
- 给定 \(\bar{z}\) 最优形式如下
\[ \gamma^{\ast}(\bar{y},\bar{z})\propto w_t(\bar{y},\bar{z})f_{y,z}(\bar{y},\bar{z})f_{y}(\bar{y}) \]
子空间与离散化的光选择函数
- \(\gamma(\bar{y},\bar{z}):\mathcal{S}\times\mathcal{S}\to\mathbb{R}\)
- 子空间:\(\gamma(\bar{y},\bar{z})\)
的一个子集
- 期望同一子空间中的子路径具有较低的差异性
- 如此就能同一子空间共享同一光选择分布
- 视子空间:\(\kappa_{\mathcal{E}}(\bar{z})\)
- 光子空间:\(\kappa_{\mathcal{L}}(\bar{y})\)
- 离散近似
- \(f_y\) 容易处理,\(f_{yz},w_t\) 使用离散矩阵 \(\Gamma\) 近似
\[ \gamma(\bar{y},\bar{z})\approx\gamma_r(\bar{y},\bar{z})= \dfrac {\Gamma(\kappa_{\mathcal{L}}(\bar{y}),\kappa_{\mathcal{E}}(\bar{z}))f_y(\bar{y})} {Q(\bar{z})} \]
- \(\Gamma\):子空间之间的光选择函数,称为子空间采样矩阵
\[ \sum_{i}\Gamma(i,j)=1 \]
- \(Q\):归一化,保证 \(\gamma\) 是个分布
\[ Q(\bar{z})=\int_{\mathcal{S}}\Gamma(\kappa_{\mathcal{L}}(\bar{y}),\kappa_{\mathcal{E}}(\bar{z}))f_y(\bar{y})\;\mathrm{d}\mu(\bar{y}) \]
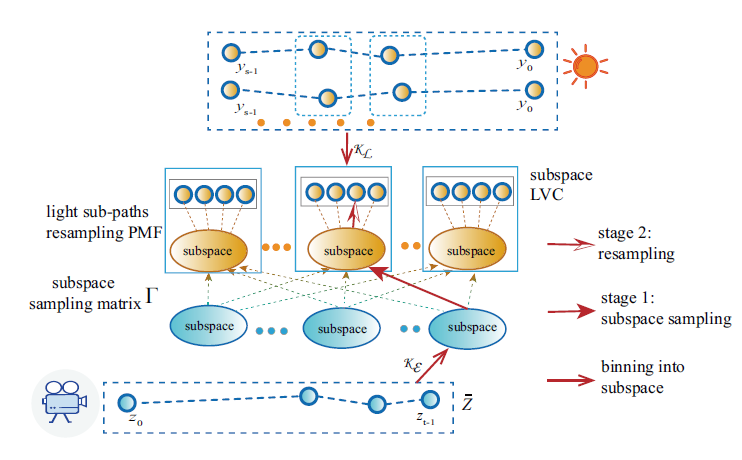
两阶段采样方法
- 阶段一:视子路 \(\bar{z}\) \(\to\) 找到视子空间 \(\kappa_{\mathcal{E}}(\bar{z})\) \(\to\) 采样光子空间 \(\Gamma(\kappa_{\mathcal{L}}(\bar{y})\vert\kappa_{\mathcal{E}}(\bar{z}))\)
- 阶段二:在 \(\kappa_{\mathcal{L}}(\bar{y})\) 中按照正比于 \(f_y(\bar{y})\) 的概率采样得到 \(\bar{y}\),与 \(\bar{z}\) 进行连接
第二阶段的重采样
- 直接采样很难满足正比于 \(f_y(\bar{y})\)
- Resampled Importance Sampling(RIS)
- RIS 流程大致如下
- 为了从目标分布 \(q\) 中生成样本,RIS 首先需要一个辅助采样分布 \(p\)
- \(p\)
可以很容易采样,并且需要满足对任何 \(q>0\) 的样本,都有 \(p>0\)
- 只要满足这些条件,\(p\) 可以被任意指定
- RIS 首先需要从分布 \(p\) 中生成多个候选样本,然后从候选样本中以正比于 \(\dfrac{q}{p}\) 的概率选择输出的样本
- 只要候选样本的规模足够大,RIS 可以产生接近目标分布的样本
- RIS 应用:\(q=f_y(\bar{y}),p=p(\bar{y})\)
- 追踪候选的光子路径是预先处理的,和 LVCBPT 类似
- 算法
- 大量的光子路首先被追踪并被 \(\kappa_{\mathcal{L}}\) 分类到各自的子空间中
- 对于一个视子路径 \(\bar{z}\),我们通过 \(\kappa_{\mathcal{E}}\) 将其分入相关的视子空间,使用矩阵 \(\Gamma\) 对相应的光子空间进行采样,并在光子空间对应的子空间 LVC 内对候选光子路径进行重采样
开销
- 相比于 LVCBPT,额外开销如下
- 对于每一个子路径执行一次子空间查询 \(\Gamma\)
- 不同子路径复用
- 两次采样分布(RIS)
- 对于每一个子路径执行一次子空间查询 \(\Gamma\)
MIS 权重
- 只需要满足 \(\sum_{t}w_t(\bar{x})=1\),那么结果就是无偏的
- 对于完整路径 \(\bar{x}=\bar{z}\bar{y}\) ,某一种采样策略 \(p_t\) 的采样概率如下
\[ \begin{aligned} p_t(\bar{x}) &=p(\bar{z})\gamma_r(\bar{y}\mid\bar{z})&(1)\\ &=p(\bar{z})\dfrac {\Gamma(\kappa_{\mathcal{L}}(\bar{y}),\kappa_{\mathcal{E}}(\bar{z}))f_y(\bar{y})} {Q(\bar{z})}\\ &\propto p(\bar{z})\Gamma(\kappa_{\mathcal{L}}(\bar{y}),\kappa_{\mathcal{E}}(\bar{z}))f_y(\bar{y})\\ \end{aligned} \]
- 以 \(p_t\) 作为 MIS 的依据,使用平衡启发式
- \(\gamma\)
计算中,重采样分布解析式难以计算(RIS 最终会趋向于 \(\propto f_y\))
- 实际采样如下,最后两步有相关性,\(f/p\) 解析式难算
\[ p(\bar{z})\Gamma(\kappa_{\mathcal{L}}(\bar{y}),\kappa_{\mathcal{E}}(\bar{z}))\cdot p(\bar{y})\cdot \dfrac{f_y(\bar{y})}{p(\bar{y})} \]
- 我们使用 \(f_y\)
来代替第二部分重采样的概率
- 是无偏的,相当于 \(\sum_{t}a_t(x)b_t(x)=1\) 使用 \(\sum_{t}a_t(x)c_t(x)=1\) 代替了
- 还得保证 \(c_t(x)\) 在不同的计算下都是一致的(近似一致性)(是个函数)
最优化子空间采样矩阵
- \(\Gamma\):用于近似 \(w_{t}f_{yz}\)
循环依赖问题
- \(\Gamma\longleftrightarrow w_t\)
- 之前工作:Variance-Aware PT
- 迭代不能取得最优值
- 原始论文假设迭代轮之间变化缓慢,迭代的方法能收敛到最值
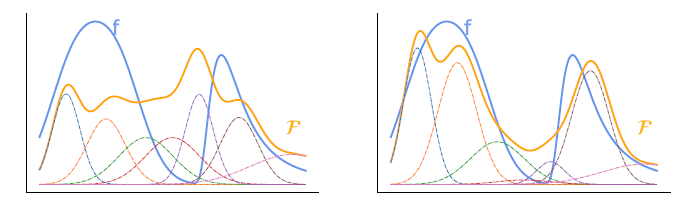
方差分析与全局最优化思想
\[ E(\hat{I}^2)=\int_{\Omega}\dfrac{f^2(\bar{x})}{\mathcal{F}(\bar{x})}\;\mathrm{d}\mu(\bar{x})\\ \]
- 平衡启发式等价于大分布采样:\(\mathcal{F}(\bar{x})=\sum_{t}p_t(\bar{x})\)
- 根据上面的式子 \((1)\),某一种采样策略 \(p_t(\bar{x})\) 将和 \(\Gamma\) 中的某一项成正比
- 于是 \(\mathcal{F}\) 将和 \(\Gamma\) 中的多个项成线性相关,记号
\[ g_{i,j}(\bar{x})=\dfrac{\partial\mathcal{F}(\bar{x})}{\partial\Gamma_{i,j}} \]
- 于是有如下式子,\(g_0\) 表示非连接策略带来的结果(例如 PT 直接打到光源)
\[ \mathcal{F}(\bar{x})=\sum_{t}p_t(\bar{x})=g_0(\bar{x})+\sum_{i,j}\left(g_{i,j}(\bar{x})\Gamma_{i,j}\right) \]
- 如此 \(\mathcal{F}\) 是多个函数
\(g_{i,j}\) 的混合,\(\Gamma_{i,j}\)
表示混合比例,此时求最优的混合比例是一个凸优化问题
- Minimum variance importance sampling via population Monte Carlo
- Variance Analysis of Multi-sample and One-sample Multiple Importance Sampling
- 实现上,预先追踪一部分光路作为训练集,使用梯度下降法最小化方差,获取最优 \(\Gamma\)
子空间划分
- 子空间对于视子路径和光子路径是共用的
- 光子路径中直接光照做特殊处理(有很多现成方法:LightCuts 方法)
- 实践上,将面光源或是环境光源依照其 uv 坐标做网格切分,每一个格子中的子路径集合是一个光子空间
- 一般子空间:通过中心子路径——距离函数的方式定义分类函数
- 中心子路径集 \(\{\bar{C_i}\}\),距离函数 \(d\),一个子路径属于离他最近的子空间
- \(\kappa\) 定义如下
\[ \kappa(\bar{y})=\mathop{\arg\min}_{i}\;d(\bar{C_i},\bar{y}) \]
- 实践中,从高贡献路径的前缀/后缀中采样中心子路径集 \(\{\bar{C_i}\}\),以适应性地提高对那些重要的路径的估计精度
距离公式
- 光子路径为例
- 距离相近的光子路径,在与相同的视子路径连接时,光选择函数 \(\gamma\) 相近
- \(\gamma=w_t\cdot f_{yz}\cdot f_y\)
- \(f_y\) 在重采样中被处理了
- \(w_t\) 过于复杂
- 试图处理 \(f_{yz}\)
- \(f_{yz}\) 影响因素:\(\rho\cdot GV\cdot\rho\)
- 可见性:子路径末端位置
- 材质项:子路径末端位置、法线、入射方向
- 几何项:子路径末端位置、法线
- 特制距离公式如下
\[ d=d_s^2+\sigma_s^2(1-\cos\theta_n)+k_d\sigma_s^2(1-\cos\theta_d) \]
- \(d_s\):空间位置距离
- \(\theta_n\):法线夹角
- \(\theta_d\):入射角夹角
- \(\sigma_s^2\):衡量场景的空间尺度
- 追踪一组完成路径,考虑所有路径顶点空间位置上的方差 \(\sigma_s^2\)
- \(k_d\) :权重,实践中发现作用不大,设置为 0~0.05
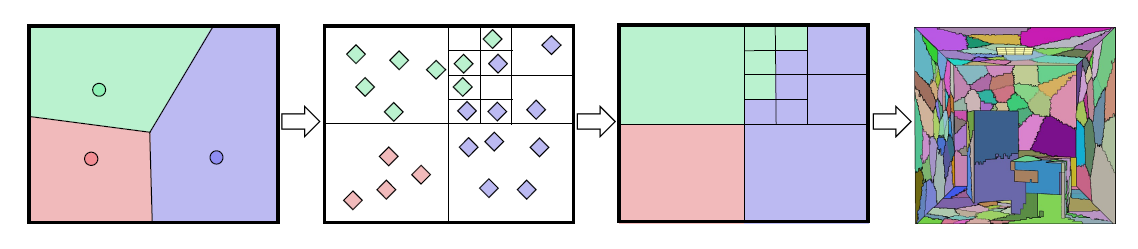
决策树拟合
- 子空间的数目量级:数百至一千
- 最近邻效率低,使用决策树拟合
- 实践
- 生成一组子路径,最近邻将子路径分入空间,并打上标记(序号)
- 使用带标记的子路径构建决策树,节点标记如下
- 决策树节点的标记为子路径标签的众数
- 如果节点不含有子路径,则与父节点在相同
- 决策树分裂
- 随机选择位置、法线、入射方向中的一个属性进行分裂
- 如果 99% 的子路径被正确分类(中众数比例大于 99%),则结束分裂
- 决策树节点的包围盒的中心值作为决策阈值
- 构建过程与可视化
子路径跨帧重用
- 重采样:候选光子路数目越多越好
- 复杂设定下无法保证每个子空间都有足够多的样本
- 跨帧重用:保证每个子空间都有足够样本
- 每一个子空间,维护一个先进先出的队列,只保存 \(M_0\) 个最新的子路径样本
- 实操:\(M_0=200\) 已经足够
算法
- BDPT/PT 打出大量完整光子路,进行子空间划分,构建 \(Q,\Gamma\)
- 进入迭代循环:
- 追踪大量光子路,缓存至对应子空间的 LVC 中
- 追踪视子路,两阶段采样法采样光子路
- 连接,计算贡献值