(论文)[2023] 基于子空间的双向路径连接渲染技术(1)

Posted on Edited on Views:
BDPT，引言，背景知识与相关工作（基础 BDPT、光子路重用 LVCBPT、概率连接思想 PCBPT）

基于子空间的双向路径连接渲染技术(1)

引言

  • 离散像素 \(I\) 的颜色与连续的图像 \(I(u,v)\) 的关系
    • \(W_e\)：相机感知函数，表示这个像素点的颜色与哪些位置的值相关

\[ I=\int W_e(u,v)I(u,v)\;\mathrm{d}u\mathrm{d}v \]

  • 光栅化：\(W_e(u,v)=\delta(u,v)\)
  • 一般认为光源 \(\text{BRDF} = 0\)，即光线打到光源上就被完全吸收
    • 因此 PT 中 camera ray 击中光源则停止追踪，\(L=L_o+L_r=L_o\)
  • BDPT：
    • 光源配置 \(\to\) 间接光占比极高
    • 路径组成复杂
  • 本文（基于 BDPT）
    • Subspace-based Probabilistic Connections for Bidirectional Path Tracing
    • BDPT：光选择过程，光选择函数
    • proxy tracing：替换中间的不好的顶点

背景知识与相关工作

渲染方程

  • 渲染方程的路径积分形式

\[ I=\int_{\Omega}f(\bar{x})\;\mathrm{d}\mu(\bar{x}) \]

  • 路径：\(x_0\) 在光源处，\(x_k\) 在摄像机上

\[ \bar{x}=x_0\cdots x_k \]

  • 面积

\[ \mathrm{d}\mu(\bar{x})=\mathrm{d}A(x_0)\cdots\mathrm{d}A(x_k) \]

  • 贡献

\[ f(\bar{x})=L_e({x}_0,{x}_1)T(\bar{x})W_e({x}_{k-1},{x}_k) \]

\[ T(\bar{x})=GV({x}_0,{x}_1)\left[\prod_{i=1}^{k-1}B({x}_{i-1},{x}_i,{x}_{i+1})GV({x}_i,{x}_{i+1})\right] \]

\[ GV({x}_i,{x}_j)=V({x}_i,{x}_j)\dfrac{\vert\cos\theta_{i,j}\vert\vert\cos\theta_{j,i}\vert}{\Vert{x}_i-{x}_j\Vert^2} \]

MIS

  • 多重重要性采样
  • 一条相同路径的采样策略可能有多个，因此需要对他们加权（权值和为 1）
  • 平衡启发式：效果上等价于使用新的分布进行采样 \(\mathcal{F}(x)\)

\[ \mathcal{F}(x)=\sum_{i}p_i(x) \]

BDPT

  • 同样的一条路径在 BDPT 中会对应多种不同的采样方式，使用 MIS 分配权重
  • 一般流程
    • 从光源和摄像头各自追踪一条子光路，随后对两条子光路上的任意一对顶点做可见性测试
    • 所有都连

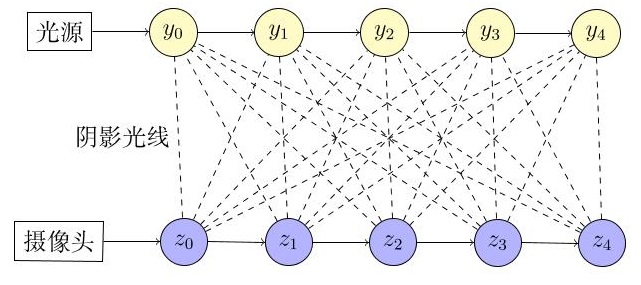
  • 子路径追踪的本质：采样得到了若干个子路径（路径前缀），pdf 的形式说明了这一点
    • 顶点数为 \(t\) 的子路径 \(\bar{z}\)
    • 有相关性

\[ p(\bar{z})=p(z_0)\prod_{i=1}^{t-1}p(z_{i-1}\to z_{i}) \]

  • 采样空间：场景表面集合 \(A\) 的任何一个笛卡尔积 \(A^{t}\)

MC 估计

  • 光子路径 \(\bar{y}\)、视子路径 \(\bar{z}\)

\[ p(\bar{x})=p(\bar{y})\cdot p(\bar{z}) \]

  • MIS：对不同的形成 \(\bar{x}\) 策略，光子路径 \(\bar{y}\)、视子路径 \(\bar{z}\) 的顶点数对 \((s,t)\)
    • 长度 \(k\)，采样策略 \(k+2\)
    • \(s+t=k+1\)

\[ I=\sum_{s,t} I_{s,t} \]

\[ I_{s,t}=\int w_{s,t}(\bar{x})f(\bar{x})\;\mathrm{d}\mu({\bar{x}}) \]

  • 平衡启发式

\[ w_{s,t}(\bar{x})=\dfrac{p_{s,t}(\bar{x})}{\sum_{s'+t'=k+1}p_{s',t'}(\bar{x})} \]

  • 传统 BDPT：一个像素单独追踪一条光子路径和视子路径

光子路重用

  • 对于不同的像素，光子路的的生成过程是一致的
    • 有相关性，因此过程中也需要更新光子路
  • LVCBPT：2 pass
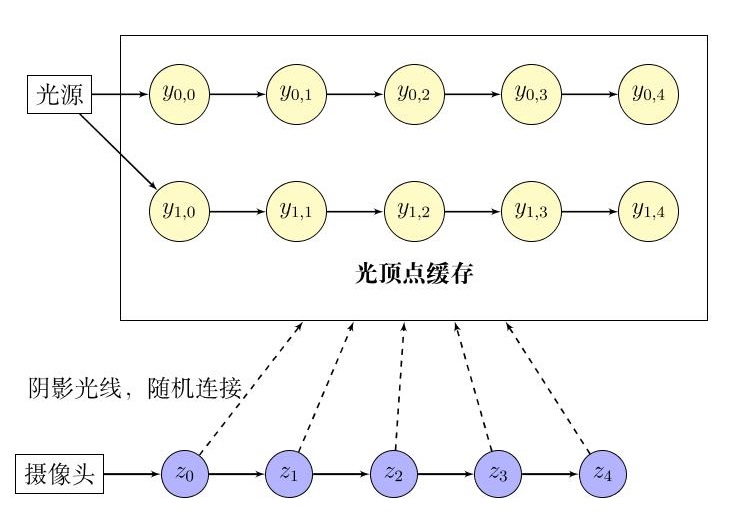
    • 第一步，追踪多条光源子光路，将追踪出的光顶点存放入光顶点缓存中
    • 第二步，追踪视线子光路，对视线子光路中的每一个视顶点，在光顶点缓存中随机选取一个光顶点进行连接
    • LVC：光顶点缓存（Light Vertex Cache）
      • \(\mathcal{S}\)

  • 对于一条路径，他的采样空间为 \(\mathcal{S}\)

MC 估计

  • 选择光子路的时候不会限制长度，只连末端
  • 采样策略：通过视子路径顶点数 \(t\) 来区分

\[ \begin{aligned} I &=\sum_{t}I_t =\sum_{t}\int w_t(\bar{x})f(\bar{x})\;\mathrm{d}\mu(\bar{x})\\ &=\sum_{t}\int_{A_t}\int_{\mathcal{S}} w_t(\bar{y}\bar{z})f(\bar{y}\bar{z})\;\mathrm{d}\mu(\bar{y})\mathrm{d}\mu(\bar{z})\\ \end{aligned} \]

  • 采样光子路的概率 \(p_r(\bar{y})=p_o(\bar{y})\cdot p_{select}(\bar{y})\)
    • 光子路被追踪并且缓存到 LVC 的概率
    • 从 LVC 中采样得到光子的概率
    • 启发：感觉在 path guiding 算法中，根本不会考虑构建构建 \(\mathcal{S}\) 的概率
  • 具体如下
    • \(M\)：每次迭代的光子路追踪次数

\[ p_o(\bar{y})=Mp(\bar{y}) \]

  • 光子路均匀采样，则有
    • 有点怪，感觉这个均匀是按照 \(\bar{y}\) 的权重加权采样，而不是说 \(n\) 条则每一条的概率为 \(\dfrac{1}{n}\)

\[ \begin{aligned} p_{select}(\bar{y}) &=1/\left({M\int_{\mathcal{S}}p(\bar{y'})\;\mathrm{d}\mu(\bar{y'})}\right)\\ &\xlongequal{?}1/\left({\int_{\mathcal{S}}p_o(\bar{y'})\;\mathrm{d}\mu(\bar{y'})}\right)\\ \end{aligned} \]

  • 合在一起可以看到，就是把追踪得到这条光子路的概率归一化之后作为采样权重
  • 实践上也可以直接取：\(p_{r}(\bar{y})=\dfrac{1}{候选光子路数目}\)
    • 这个是 \(n\) 条则每一条的概率为 \(\dfrac{1}{n}\)
  • 确切的来说只需要 \(p_r(\bar{y})\) 对所有的光子路求积分为 1 即可

概率连接思想

  • 连接的时候，可以认为是计算不同的光子路 \(\bar{y}\) 的加权贡献值
    • 类似于 path guiding

\[ I(\bar{z})=\int_{\mathcal{S}}w_t(\bar{y}\bar{z})f(\bar{y}\bar{z})\;\mathrm{d}\mu(\bar{y}) \]

  • LVCBPT 是均匀的选择，如何更好的选择？ \(\to\) 光选择问题

PCBPT

  • Key Idea：不考虑 MIS 权重函数的影响，认为选择光子路的概率应当正比于视子路与光子路连接形成的完整光路的贡献值
  • 每一个视子路的光选择分布都会不太一样，但是实现上，末端相近的视子路使用相同的分布（PMF Record）
    • KD 树等数据结构
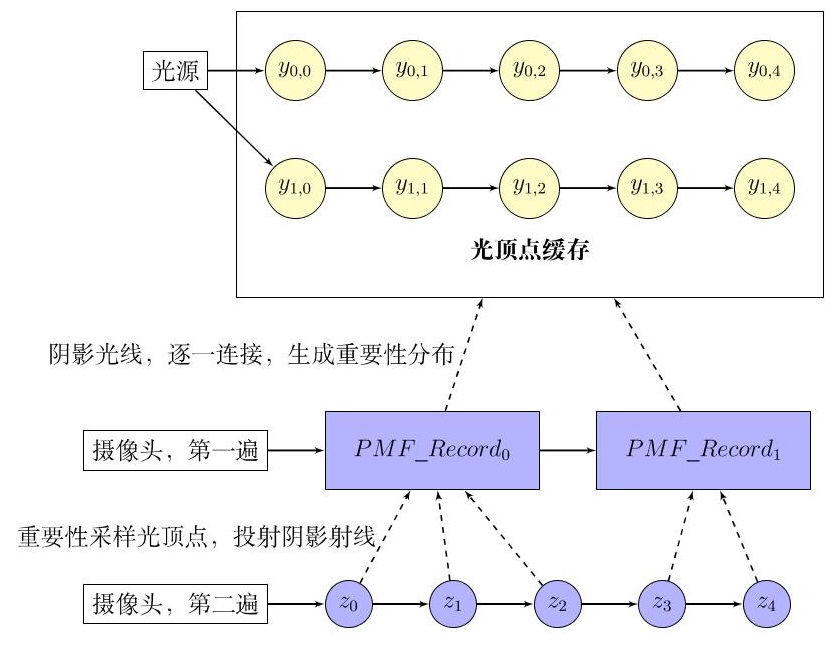
  • 3 Pass
    • 追踪多条光源子光路，将追踪出的光顶点放人光顶点缓存中
    • 追踪少量视线子光路，每个视顶点与光顶点缓存中每一个光顶点连接，生成 PMF Record
    • 追踪视线子光路，为每个视顶点找到合适的 PMF Record，随后重要性采样出光顶点，与其连接

  • 效率能够达到 BDPT 的 3x~4x
  • 问题：
    • PMF Record 构建慢
      • 每一条光子路都需要做可见性测试
      • 光子路更新会使其重建
    • 算法开销正比于光子路个数，因此光子路个数少（100-200）
      • 早期渲染带来巨大的像素间相关性
    • PMF Record 存储的 KD 查询慢
    • 未考虑 MIS，因此不是最优的

其他相关工作

  • 多光源方法
    • Lightcuts、Lightslice
    • 可见性、方差最小化
      • VisibilityCluster
      • Bayesian online regression for adaptive direct illumination sampling
  • Path Guiding
  • Photon Mapping
  • ReSTIR