(论文)[2022-SIG] EARS: Efficiency-Aware Russian Roulette and Splitting(1)

Posted on 2023-07-10 Edited on 2023-11-01 Views:

RRS 理论部分（相关工作、背景知识、RRS 理论推导）

EARS

introduction

大部分 PT 算法中，很多计算都被浪费在追踪低贡献的长路径中
RRS：Russian roulette (RR) and splitting
- RR：提前终止
- S：相同前缀产生多个后缀
分裂在高方差处需要多一些
- 例如焦散的 diffuse 表面
- ADDRS 只考虑了期望贡献值，但是没有考虑方差，只能保证这些路径仍然存在，但是不能分裂

background

渲染方程

\[ I_{\text{px}}=\int f_{\text{px}}(\bar{\mathrm{z}})\;\mathrm{d}\bar{\mathrm{z}} \]

MC 无偏估计

\[ \left\langle I_{\text{px}}\right\rangle=\dfrac{f_{\text{px}}(\bar{\mathrm{z}})}{p(\bar{\mathrm{z}})} \]

效率：方差、计算代价乘积的倒数
- 积分形式如下
- 计算代价的一个启发式：追踪的光线数目

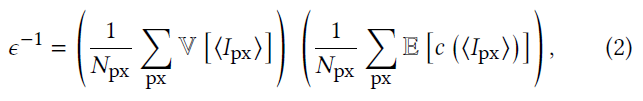
前缀路径：\(\bar{\mathrm{x}}_k=\mathrm{x}_0\cdots \mathrm{x}_k\)
贡献值
- \(t_{\text{px}}\)：throughout
  - the product of sensor response, pixel contribution, BSDFs, and geometry terms

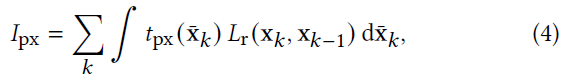
前缀权重

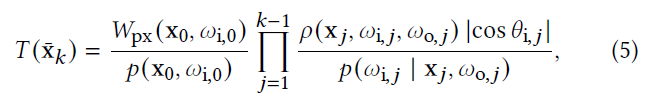
MC 估计

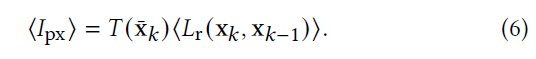
Russian roulette (RR)
- \(q\)：survival probability

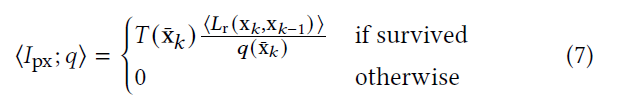
Splitting：相同前缀 \(\bar{\mathrm{x}}_k\) 生成 \(n(\bar{\mathrm{x}}_k)\) 个独立的后缀
- \(\left\langle L_{\text{r}}\right\rangle\) 方差比较大时，效果比较好

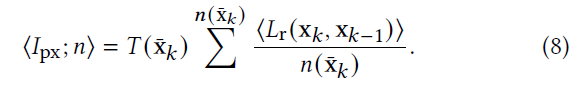
Russian roulette and splitting (RRS)：RR+Splitting，结合到同一个框架里

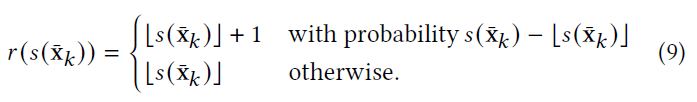
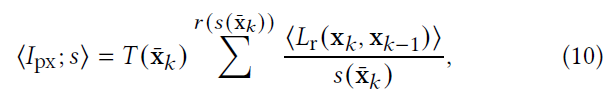
RRS 无偏性
- 当 \(\lfloor{s(\bar{\mathrm{x}}_k)}\rfloor={s(\bar{\mathrm{x}}_k)}\) 时，显然成立，考虑 \(\ne\) 情况

\[ \begin{aligned} E\left[\left\langle I_{\text{px}};s\right\rangle\right] &= \left({s(\bar{\mathrm{x}}_k)}-\lfloor{s(\bar{\mathrm{x}}_k)}\rfloor\right) \sum^{\lfloor{s(\bar{\mathrm{x}}_k)}\rfloor+1} \dfrac {E\left[\left\langle T(\bar{\mathrm{x}}_k)L_{\text{r}}(\bar{\mathrm{x}}_k,\bar{\mathrm{x}}_{k-1})\right\rangle\right]} {\lfloor{s(\bar{\mathrm{x}}_k)}\rfloor+1}\\ &\quad+ \left(1+\lfloor{s(\bar{\mathrm{x}}_k)}\rfloor-{s(\bar{\mathrm{x}}_k)}\right) \sum^{\lfloor{s(\bar{\mathrm{x}}_k)}\rfloor} \dfrac {E\left[\left\langle T(\bar{\mathrm{x}}_k)L_{\text{r}}(\bar{\mathrm{x}}_k,\bar{\mathrm{x}}_{k-1})\right\rangle\right]} {\lfloor{s(\bar{\mathrm{x}}_k)}\rfloor}\\ &= \left({s(\bar{\mathrm{x}}_k)}-\lfloor{s(\bar{\mathrm{x}}_k)}\rfloor\right) \sum^{\lfloor{s(\bar{\mathrm{x}}_k)}\rfloor+1} \dfrac {I_{\text{px}}} {\lfloor{s(\bar{\mathrm{x}}_k)}\rfloor+1} + \left(1+\lfloor{s(\bar{\mathrm{x}}_k)}\rfloor-{s(\bar{\mathrm{x}}_k)}\right) \sum^{\lfloor{s(\bar{\mathrm{x}}_k)}\rfloor} \dfrac {I_{\text{px}}} {\lfloor{s(\bar{\mathrm{x}}_k)}\rfloor}\\ &=\left({s(\bar{\mathrm{x}}_k)}-\lfloor{s(\bar{\mathrm{x}}_k)}\rfloor\right){I_{\text{px}}}+\left(1+\lfloor{s(\bar{\mathrm{x}}_k)}\rfloor-{s(\bar{\mathrm{x}}_k)}\right){I_{\text{px}}}\\ &={I_{\text{px}}} \end{aligned} \]

Nested RRS
- 每个路径节点都可以有 RRS
- \(\left\langle L_r\right\rangle\)：primary estimator（1 sample per vertex）

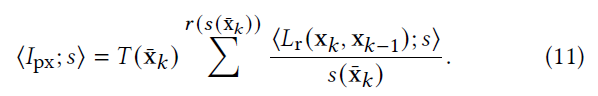
此时 throughout 如下

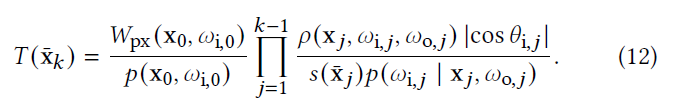
Efficiency-Aware RRS

问题：当给定路径前缀 \(\bar{\mathrm{x}}_k\) 时，求解得到最优的 RRS 值
抽象问题，前缀 \(x\)，后缀 \(y\)

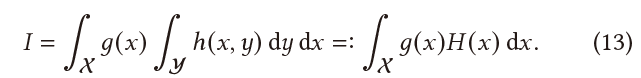
\[ \langle{I}\rangle=\dfrac{g(x_j)}{p(x_j)}\sum_{i=1}^{n(x_j)}\dfrac{h(x_j,y_i)}{n(x_j)p(x_j,y_i)} \]

Optimal splitting

\(n(x):\mathcal{X}\to\mathbb{N}\)
\(y_i\) 独立

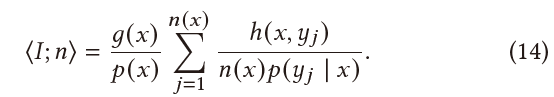
objective：最大化效率

\[ \mathop{\arg\max}_{n}\;\mathbb{V}\left[\left\langle I;n\right\rangle\right]\mathbb{E}\left[c\left(\left\langle I;n\right\rangle\right)\right] \]

方差

方差（条件期望展开）：\(V=VE_y+EV_y\)
- \(V_{\mathcal{Y}}\)：不加 splitting 的方差

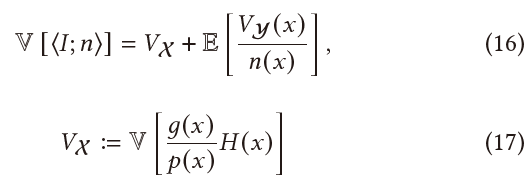
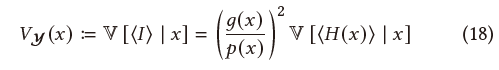\[ \langle{H(x)}\rangle=\dfrac{h(x,y)}{p(y\mid x)} \]

1997 年论文原始公式如下

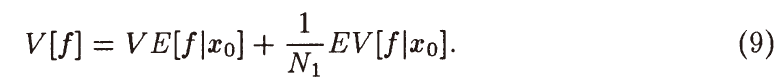
cost

假设：代价 \(\propto\) 发射的光线数目（样本数）
（期望）代价 = 前缀 + 后缀
- 这里的内层，\(\langle{H(x)}\rangle\) 其实还有一个 \(E\)（期望）

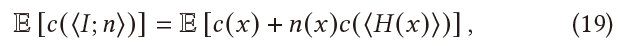
优化

假设：\(n(x)\) 是实数
- 这样可以微分、凸优化
- 引入偏差：最终需要做 round 操作
实数定义上，效率函数关于 \(n(x)\) 是凸函数，有唯一的全局最优值
- \(ax+\dfrac{b}{x}+c,x>0\)
- 如何求得？偏导为 0

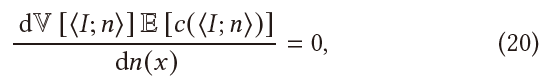
有解析解，但是求解不现实
- 统计量难以估计
- 递归依赖，RRS 发生在各个阶段
- 解析解如下

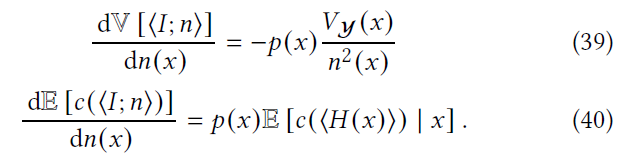
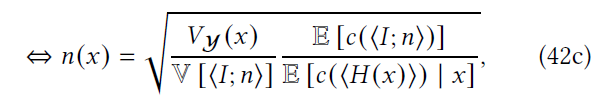
\({\color{red}p(x)}\) 哪里来的？
- 解释：期望展开对可能的数据点求导
- \(n(x)\)：一个 \(x\) 对应一个 \(n(x)\)
- 离散展开

\[ \dfrac{\partial{V[\langle{I;n}\rangle]}}{\partial n(x)} =\dfrac{\partial{E\left[\dfrac{V_{\mathcal{Y}}(x)}{n(x)}\right]}}{\partial n(x)} =\dfrac{\partial{\left(\sum_{i}\dfrac{V_{\mathcal{Y}}(x_i)}{n(x_i)}p(x_i)\right)}}{\partial n(x_i)} =-\dfrac{V_{\mathcal{Y}}(x_i)p(x_i)}{n^2(x_i)} \]

\({\color{red}p(x)}\) 哪里来的？
- 泛函：\(n(x)\) 是一个函数

\[ f(n)=E\left[\dfrac{V_{\mathcal{Y}}(x)}{n(x)}\right]=\int\dfrac{V_{\mathcal{Y}}(x)}{n(x)}p(x)\;\mathrm{d}x \]

\[ \begin{aligned} f(n(x)+\delta n(x))-f(n(x)) &=\int\dfrac{V_{\mathcal{Y}}(x)}{n(x)+\delta n(x)}p(x)\;\mathrm{d}x-\int\dfrac{V_{\mathcal{Y}}(x)}{n(x)}p(x)\;\mathrm{d}x\\ &=\int-\dfrac{V_{\mathcal{Y}}(x)p(x)}{n(x)(n(x)+\delta n(x))}\delta n(x)\;\mathrm{d}x\\ &=\left\langle-\dfrac{V_{\mathcal{Y}}(x)p(x)}{n^2(x)},\delta n(x)\right\rangle+o(\delta n(x))\\ \end{aligned} \]

不动点迭代

Fixed-point iteration

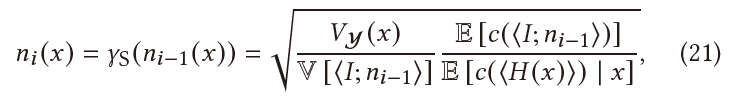
收敛性分析
- 条件：自身映射、连续、导数小于1
  - 这里要求 \(D=(t,+\infty)\) 的形式
- 如果初始化点 \(x\notin\) 定义域 \(D\)，增加如下条件
  - \(x_0\notin D\)，迭代几步之后进入 \(D\)
  - \(D=(t,+\infty)\Rightarrow\) 的条件下，就是要求 \(g(x)>x,\forall x\le t(/\forall x\notin D)\)
  - 这个作用是将初始条件放松到任意正值
TODO：附录 C

结合 RR

Optimal RR

只考虑 RR，不考虑 S
- RR 必然增加方差
方差如下（推导）

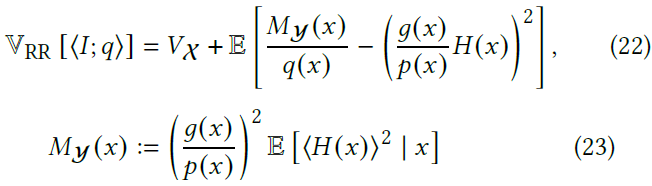
同样为凸函数
此时不动点迭代函数如下
- 推导过程和上面一样，求偏导 \(=0\)

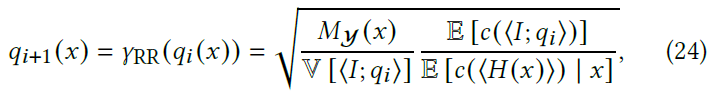
Optimal RRS

联合优化
分段函数
- 将二者用统一的方式表达

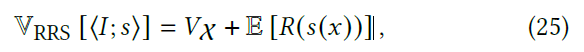
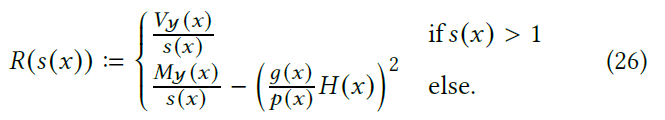
此时效率函数 \(\epsilon^{-1}\) 还是凸函数
方差
- 从定义上看，二者显然都是递减的
- \(s(x)=1\) 时，值相等（连续）
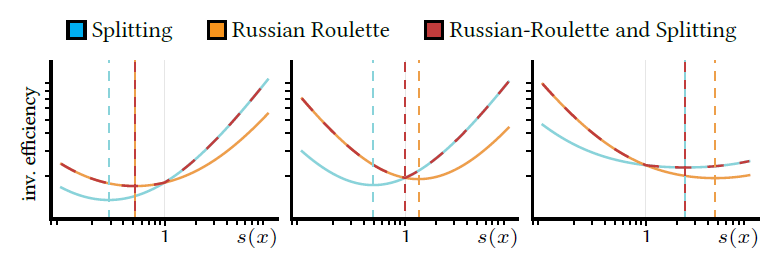
\(\epsilon^{-1}\)
- \(s(x)=1\) 时，值相等（连续）
- \(x<1\) 时，RR 值更大；\(x>1\) 时，RR 值更小（牛的）
  - 代价函数定义相同，只需要比较方差项
  - 式子 \((26)\)，上面定义为 \(A\)，下面定义为 \(B\)

\[ \begin{aligned} E[A]-E[B] &=E\left[\dfrac{V_{\mathcal{Y}}(x)}{s(x)}-\dfrac{M_{\mathcal{Y}}(x)}{s(x)}+\left(\dfrac{g(x)}{p(x)}H(x)\right)^2\right]\\ =&E\left[\dfrac{1}{s(x)}(V_{\mathcal{Y}}(x)-M_{\mathcal{Y}}(x))\right]+E\left[\left(\dfrac{g(x)}{p(x)}H(x)\right)^2\right]\\ =&E\left[-\dfrac{1}{s(x)}\left(\dfrac{g(x)}{p(x)}H(x)\right)^2\right]+E\left[\left(\dfrac{g(x)}{p(x)}H(x)\right)^2\right]\\ =&E\left[\left(\dfrac{s(x)-1}{s(x)}\right)\left(\dfrac{g(x)}{p(x)}H(x)\right)^2\right] \end{aligned} \]

分类讨论：根据上面两个条件，对最优值的位置分类讨论，发现都是凸函数
- 交点一阶导递增

算法
- 首先计算分裂因子 \(n(x)\)，如果结果大于 \(1\)，那么就是最优值
- 否则计算 RR 值，并将结果 clamp 到 \(\le1\)（恰好为 \(1\) 取到最值）

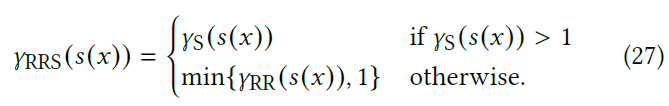
看到代码里面优先 RR

// src/integrators/path/recursive_path.cpp:L416
const Float splittingFactorS = calcS();
const Float splittingFactorR = calcR();

if (splittingFactorR > 1) {
    if (splittingFactorS < 1) {
        return clamp(1);
    } else {
        return clamp(splittingFactorS);
    }
} else {
    return clamp(splittingFactorR);
}

(论文)[2022-SIG] EARS: Efficiency-Aware Russian Roulette and Splitting(1)

EARS

introduction

相关工作

Albedo-based

Approximated contributions

Efficiency analysis

Adaptive sampling

Fixed-point iterations in rendering