glm 库的一些知识

Posted on Edited on In Views:
OpenGL 数据排布、glm 矩阵列优先、glm 变换使用示例

glm 库

OpenGL 数据排布

  • OpenGL 的数据排布是列优先的，例如如下的矩阵

\[ M=\begin{bmatrix}a & b \\c & d \end{bmatrix} \]

  • 在内存中的数据排布是 \(a,c,b,d\)，也就是说具体如下

\[ \begin{array}{c} M[0][0]=a\\ M[0][1]=c\\ M[1][0]=b\\ M[1][1]=d\\ \end{array} \]

  • 第一个下标表示第几列，第二个下标表示第几行
  • 这和我们平常 C++ 的数据排布是不一样的，我们平常使用的数组是行优先的

平移变换的例子

  • 平移变换的矩阵如下

\[ T=\begin{bmatrix} 1 & 0 & 0 & a\\ 0 & 1 & 0 & b\\ 0 & 0 & 1 & c\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \]

  • \(T\cdot x\) 表示将点 \(x\) 平移 \((a,b,c)\)
  • 以 ogl-intro 中的代码为例，我们在 01-ebo 中进行修改
  • 原始效果如下

  • 如何将它向右平移 0.5 个单位

  • 回忆 OpenGL 的 NDC 坐标系（左手系），正方向

    • x：朝右

    • y：朝上

    • z：朝屏幕里面

  • 构造的矩阵应该如下

\[ T=\begin{bmatrix} 1 & 0 & 0 & 0.5\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \]

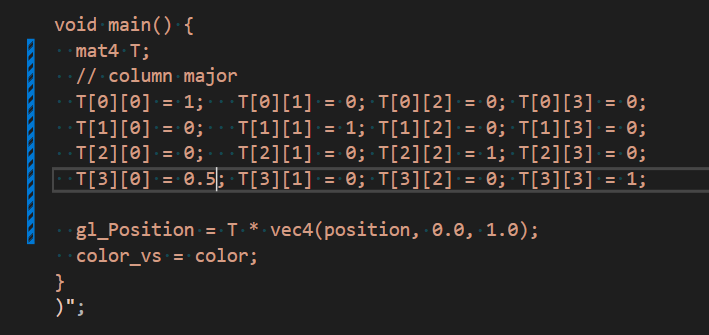
  • 修改 vertex shader，左乘变换矩阵
1
2
// 修改 vertex shader
static const char *vertex_shader_text;
1
2
3
4
5
6
7
8
9
// 关键代码如下，注意是列优先的
mat4 T;
// column major
T[0][0] = 1;   T[0][1] = 0; T[0][2] = 0; T[0][3] = 0;
T[1][0] = 0;   T[1][1] = 1; T[1][2] = 0; T[1][3] = 0;
T[2][0] = 0;   T[2][1] = 0; T[2][2] = 1; T[2][3] = 0;
T[3][0] = 0.5; T[3][1] = 0; T[3][2] = 0; T[3][3] = 1;

gl_Position = T * vec4(position, 0.0, 1.0);

  • 结果如下
img
  • 如果我们每次都需要自己去进行行优先转为列优先的操作的话，就会很麻烦
  • 不用担心，glm 库为我们做了这个操作

glm 库

(1) 列优先排布

  • glm 库是表示的矩阵是列优先的
    • 也就是说，如果使用下标索引方式的话
      • 第一个下标表示列索引
      • 第二个下标表示行索引
    • 和 OpenGL 适配的
1
2
3
4
5
6
7
8
9
10
11
12
13
// 定义一个输出函数
// 如果 transpose = true，则将其理解为列优先的矩阵
void print_mat4(glm::fmat4& m, bool transpose = false) {
    // glm is column-major
    std::cout << "\n[Log: print_mat4()]" << std::endl;
    for (int i = 0; i < 4; ++i) {
        for (int j = 0; j < 4; ++j) {
            float num = transpose ? m[j][i] : m[i][j];
            std::cout << " " << num;
        }
        std::cout << std::endl;
    }
}
  • 例如平移变换，结果如下
1
2
3
4
5
6
7
8
9
10
glm::fmat4 m3 = glm::translate(
    glm::fmat4(1.0f),            // 原始变换矩阵初始化为 I
    glm::fvec3(1.0f, 2.0f, 3.0f) // 平移量
);
print_mat4(m3);
// 输出结果如下
// 1 0 0 0
// 0 1 0 0
// 0 0 1 0
// 1 2 3 1
  • 因此他表达的实际矩阵如下
1
2
3
4
5
6
print_mat4(m3, true); // true 表示将其理解为列优先表示方式
// 输出结果如下
// 1 0 0 1
// 0 1 0 2
// 0 0 1 3
// 0 0 0 1

(2) glm 乘法

  • 首先需要理解，矩阵表示是列优先的，然后就是普通的矩阵乘法了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 初始化为全 0 的矩阵
glm::fmat4 m4 = glm::fmat4(0.0f);
// 设置第 0 列第 0 行的元素为 1，设置第 0 列第 1 行的元素为 2
m4[0][0] = 1.0f; m4[0][1] = 2.0f;

// 初始化为全 0 的矩阵
glm::fmat4 m5 = glm::fmat4(0.0f);
// 设置第 0 列第 0 行的元素为 1，设置第 1 列第 0 行的元素为 2
m5[0][0] = 1.0f; m5[1][0] = 2.0f;

glm::fmat4 m6 = m4 * m5;
print_mat4(m4, true);
print_mat4(m5, true);
print_mat4(m6, true);
  • 输出结果如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
[Log: print_mat4()]
1 0 0 0
2 0 0 0
0 0 0 0
0 0 0 0

[Log: print_mat4()]
1 2 0 0
0 0 0 0
0 0 0 0
0 0 0 0

[Log: print_mat4()]
1 2 0 0
2 4 0 0
0 0 0 0
0 0 0 0

(3) 变换顺序

  • 我们在 ogl-intro 中的 02-uniform 中进行修改，用作示例
  • 修改如下函数
1
glm::mat4 calculate_transform(float aspect);
  • 我们不进行模型变换，修改代码如下，得到结果图
    • 设置模型变换为单位矩阵 \(I\)
1
2
3
4
5
6
glm::mat4 calculate_transform(float aspect) {
    glm::mat4 model = glm::identity<glm::mat4>();
    glm::mat4 projection = glm::ortho(
        -aspect, aspect, -1.0f, 1.0f);
    return projection * model;
}

  • 现在我们想得到如下的结果，将这个头像顺时针旋转 90 度，然后向右平移 0.5 个单位长度，如下图所示

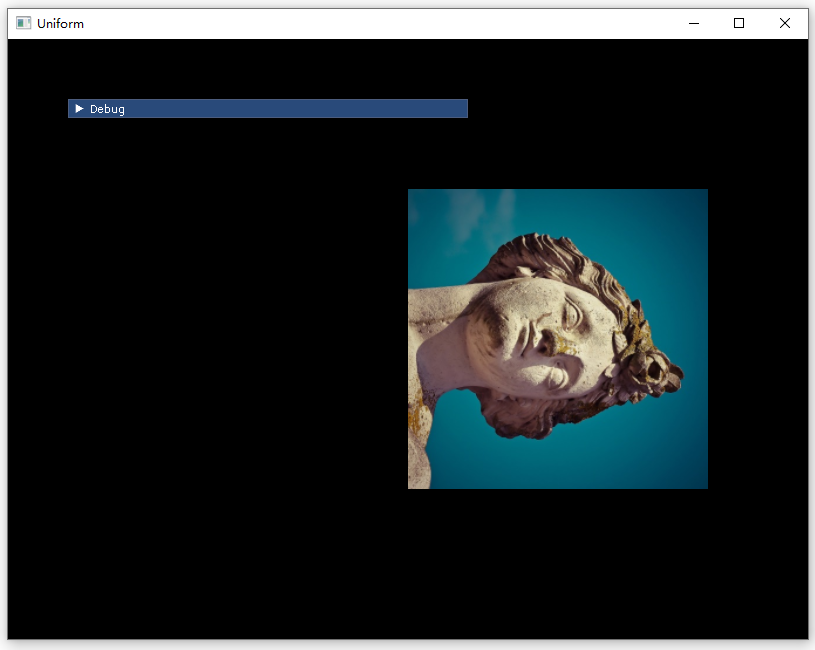
方法1：直接构建

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
glm::mat4 rotation = glm::identity<glm::mat4>();
constexpr float theta = -0.5f * glm ::pi<float>();
float cos_theta = glm::cos(theta);
float sin_theta = glm::sin(theta);
// 第一个索引下标表示第几列
// 第二个索引下标表示第几行
rotation[0][0] = cos_theta;
rotation[1][0] = -sin_theta;
rotation[0][1] = sin_theta;
rotation[1][1] = cos_theta;

glm::mat4 translation = glm::identity<glm::mat4>();
// 注意行列索引
translation[3][0] = 0.5f;

glm::mat4 model = translation * rotation;

  • 注意点：第一个索引下标表示第几列，第二个索引下标表示第几行

  • 旋转矩阵：具体形式见上课 PPT《几何变换》中的三维几何变换章节

    • 角度是弧度制
    • 课程中推导的矩阵是右手系下的矩阵变换
      • OpenGL 在 NDC 之后是左手系，之前实现为左手系和右手系都可以
      • glm 库中默认为右手系
    • 顺时针旋转 90 度
      • 注意这里的顺时针/逆时针和左右手系相关，四指转向的方向为逆时针
      • 因此 rotate 矩阵的构建不需要判断是左手系还是右手系（可以查看源码）
        • 抵消了
    • 课上推导的是以逆时针为正，因此最后的 \(\theta=-90\)

  • 右手系：xyz 轴满足右手定则

    • 右手 4 指从 x 轴正方向转向 y 轴正方向（4指张开到合上）
    • z 轴正方向刚好是大拇指的方向

方法2：利用内置函数构建

1
2
3
4
5
6
7
8
// 初始矩阵
glm::mat4 model = glm::identity<glm::mat4>();
constexpr float theta = -0.5f * glm ::pi<float>();

// 旋转变换
model = glm::rotate(model, theta, glm::vec3(0, 0, 1.0f));
// 平移变换
model = glm::translate(model, glm::vec3(0.5f, 0, 0));
  • 我们会发现，这样的结果是不正确的

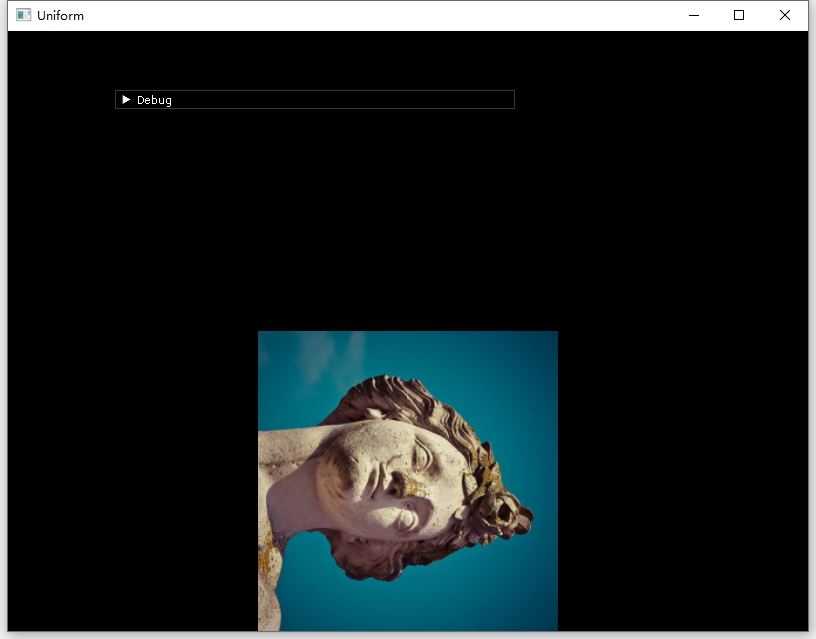
  • 查看源码发现，glm 库的变换矩阵都是在原有矩阵的基础上右乘当前变换

    • 例如 rotate()

    • 文件：glm/extmatrix_transform.inl

  • 因此相当于是先做了当前变换，再进行原来的变换矩阵

  • 因此，如果调用内置函数的话，后进行的变换应该先调用

1
2
3
4
5
glm::mat4 model = glm::identity<glm::mat4>();
constexpr float theta = -0.5f * glm ::pi<float>();

model = glm::translate(model, glm::vec3(0.5f, 0, 0));
model = glm::rotate(model, theta, glm::vec3(0, 0, 1.0f));

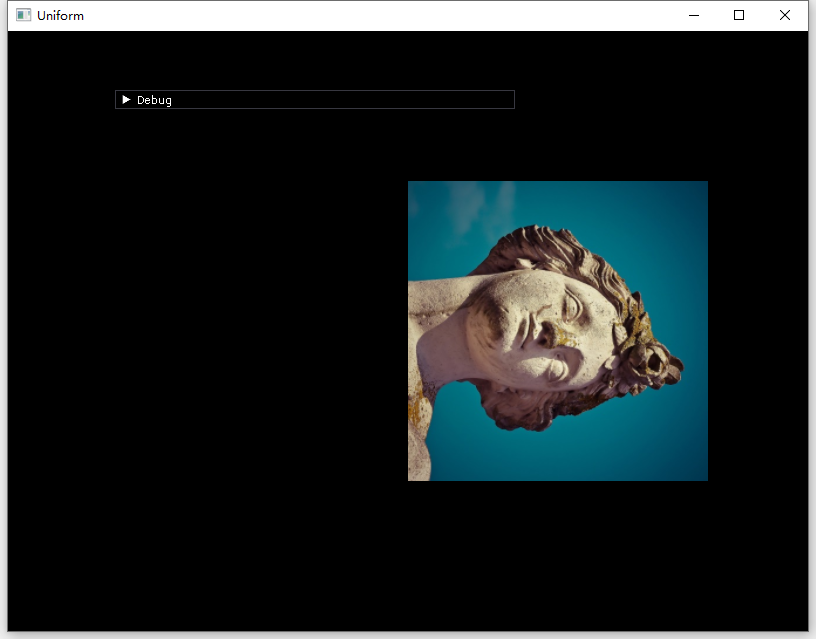
(4) 细节

  • 注意齐次坐标需要除以 \(w\)，否则可能没有归一化