算法设计与分析.08.NP 完全性理论 (4)

Posted on Edited on In Views:
求解 NPC 问题；树上问题，平面图问题，近似算法，指数算法

NP 完全性理论 (4)

  • intractability

求解 NPC 问题

  • 实际设计算法
    • 只能解决部分实例
    • 牺牲最优性
    • 可接受非多项式时间
  • 策略
    • 特殊情形
    • 近似算法、启发式算法
    • 优化指数级别算法

树

  • 树上问题的特例

树上的独立集

  • 点数最多
  • 观察：如果 v 是叶子节点，则存在一个最大独立集，包含这个节点

贪心算法

  • 适用于森林（树的集合）
  • 算法：将叶子节点加入独立集，删除叶子节点及其父节点之后，重复上面步骤
  • \(O(n)\)

最大权重独立集

  • 每一个节点都带权，找到一个权重和最大的独立集（不一定点数最多）
  • 树上 DP
  • \(OPT_{in}(r)\) ：子树 \(r\) 包含根节点的最大权重独立集
  • \(OPT_{out}(r)\) ：子树 \(r\) 不包含根节点的最大权重独立集
  • 原始问题：\(\max\{OPT_{in}(R),OPT_{out}(R)\}\)
  • 转移方程

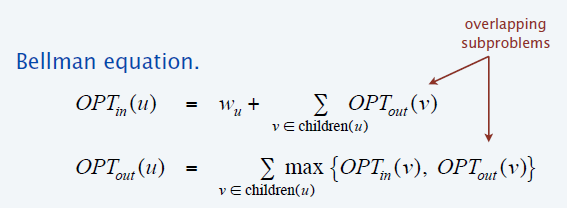
  • 实现：树的后序遍历

树的优势

  • 能够将原始问题划分为若干不相关的子问题
    • 通过某个节点断开
  • 普通图不行

平面图

  • 同构于某个在平面上没有两条边相交的图
  • 没有同构于 \(K_{3,3},K_{5}\) 的子图
  • 判断是否为平面图：\(O(n)\)
  • Efficient Planarity Testing
    • [Hopcroft–Tarjan 1974]
  • 简单平面图的性质：\(m\le3n\)

平面图3着色

  • 顶点着色
  • 平面区域3着色 \(\equiv_{p}\) 平面图3着色

  • 平面图3着色 \(\in\) NPC
    • 图3着色 \(\le_{p}\) 平面图3着色
  • 平面图3着色 \(\in\) NP 是显然的
  • 如何对任意实例 \(G\) 构造一个平面图

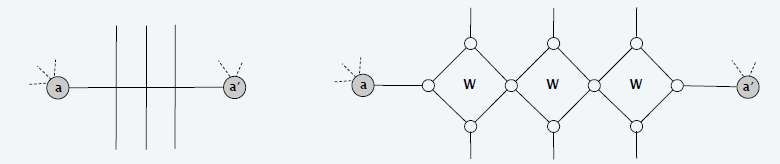
构造

  • gadget

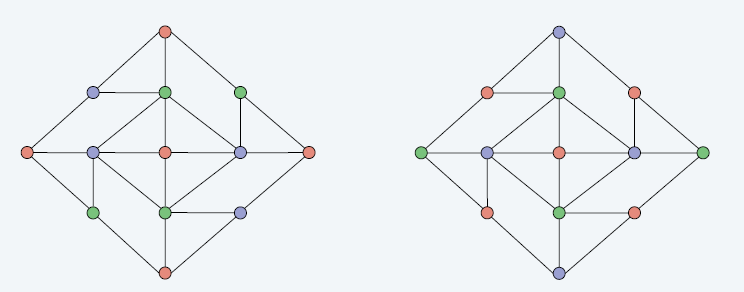
  • 对于如上的 gadget，只有上面两种 3 着色方案
    • 从中间开始向外着色
    • 都保证对角的两个点着色相同（最左最右，最上最下）
  • 对于任意的一个交叉进行如下构造

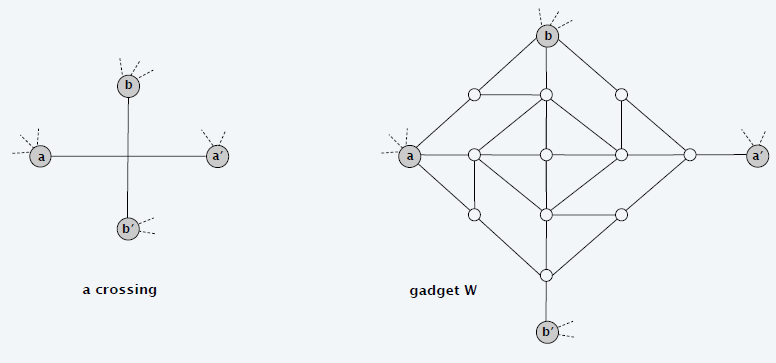
  • 如果有多个交叉，则进行连接

平面图k着色

  • Every planar map is 4-colorable
    • [Appel–Haken 1976]
    • \(O(n^4)\)
  • First major theorem to be proved using computer.
  • 现在的最优算法
    • 平面图4着色：\(O(n^2)\)
    • 平面图5着色：\(O(n)\)

特殊图

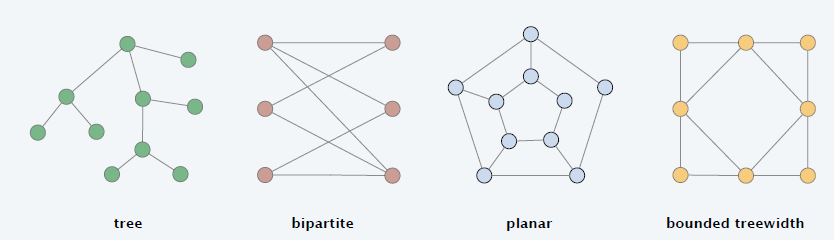
  • bounded treewidth

近似算法

点覆盖

  • k-近似算法
    • 多项式时间
    • 能够处理任意输入
    • 算法找到的结果是最优解的 \(k\) 比率
  • 例如，点覆盖2-近似算法
    • 找到的点数 \(\le\) 2x最小点覆盖的点数

贪心算法

  • 随机找和当前选中的点不相关联的边，加入这些顶点

  • \(O(m+n)\)
  • 是 2-近似算法
  • \(S'\)：最小点覆盖
  • 算法：\(\vert{S}\vert=2\vert{M}\vert\le2\vert{S'}\vert\)
    • 任意点覆盖 \(S_0\)，任意匹配 \(M_0\)
    • \(\vert{M_0}\vert\le\vert{S_0}\vert\)

k-近似算法

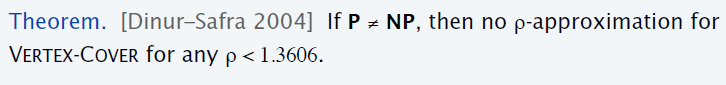
  • 猜想：不存在 \(\rho<2\)

背包问题

  • NPC
    • 子集和 \(\le_{p}\) 背包问题
  • 输入规模：\(n,\log W\)

DP1

  • \(OPT(i,w)\)：前 i 个物体，重量限制为 w 的最大价值
  • 原始问题：\(OPT(n,w)\)

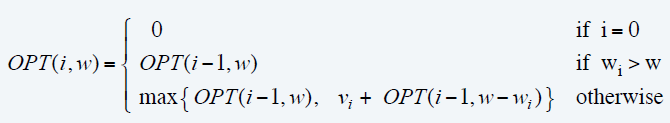
  • \(O(nW)\)
  • 当 \(w_i\) 很小的时候，可以认为是多项式时间的

DP2

  • \(OPT(i,v)\)：前 i 个物体，达到价值 v 的最小权重
  • 原始问题：最大的 v 满足 \(OPT(n,v)\le W\)

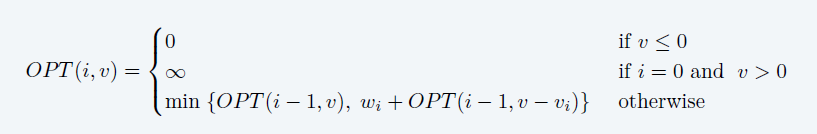
  • \(O(n\cdot nv_{max})=O(n^2v_{max})\)
  • 当 \(v_i\) 很小的时候，可以认为是多项式时间的

近似算法

  • \(\epsilon\in(0,1]\)
  • \(v_{max}\)
  • \(\theta=\dfrac{\epsilon v_{max}}{2n}\)：放缩因子

\[ \bar{v}_i=\lceil\dfrac{v_i}{\theta}\rceil\theta,\hat{v_i}=\lceil\dfrac{v_i}{\theta}\rceil \]

  • 使用 \(\bar{v}_i,\hat{v}_i\) 两者是等价的
  • 直观
    • \(\bar{v}\) 是近似的，结果也是近似最优的
    • \(\hat{v}\) 比较小，DP2 算法较快
  • 使用 \(\bar{v}\) 是 \((1+\epsilon)\)-近似的
    • 价值不是整数如何处理
    • \(\theta=\lfloor\dfrac{\epsilon v_{max}}{2n}\rfloor\)（证明的时候倒数第二行换成 \(\le\) ）
  • 原始问题可行解 \(S^{\ast}\)，\(\bar{v}\) 的可行解 \(S\)

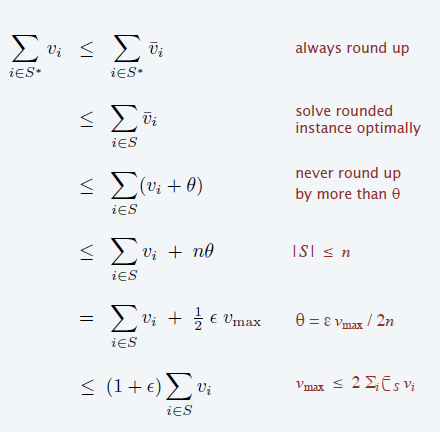
  • 等价性：\(\hat{v}\) 也满足
  • \(O(n^2\hat{v}_{max})=O(n^3/\epsilon)\)

指数算法

3SAT

  • \(n\) 个变元，\(m\) 个语句
  • 暴力枚举：\(O((m+n)2^n)\)

递归算法

  • 分配律

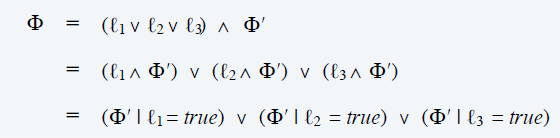
  • 复杂度

\[ \begin{array}{c} T(n)\le3T(n-1)+poly(n)\\ \Rightarrow T(n)=O(poly(n)3^{n}) \end{array} \]

  • 上面 3 种情况不是互斥的，修改为互斥的情况

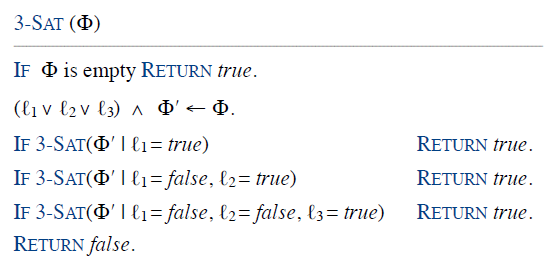
  • 这样让子问题不重叠，效率更高

\[ \begin{array}{c} T(n)\le3T(n-1)+T(n-2)+T(n-3)+O(m+n)\\ \Rightarrow T(n)=O(1.84^{n}) \end{array} \]

  • \(1.84:r^3=r^2+r+1\)
  • 最优：\(O(1.33334^{n})\)
  • 其他算法
    • DPPL：Highly-effective backtracking procedure.
    • Chaff：sota

TSP

  • traveling salesperson problem：货郎问题
  • 完全图中找到权重小于等于 D 的哈密顿回路
  • 哈密顿回路 \(\le_{p}\) TSP
    • 有边：权重 1
    • 无边：权重 2
  • DP： TSP can be solved in \(O(n^22^n)\) time.
    • [Held–Karp, Bellman 1962]

DP

  • \(c(s,v,X)\)：从 s 出发，经过 X 中所有的点有且只有一次，到达 v 的最小代价
    • \(v\ne s\)
  • 原始问题

\[ \min_{v\in V}\{c(s,v,V)+c(v,s)\} \]

  • 转移方程

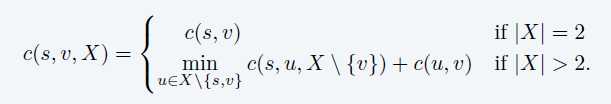
  • 子问题个数：\(\le n2^n\)
    • 子集个数：\(2^n\)
    • 每个子集选择一个终点

Euclidean TSP

  • 距离函数使用欧拉函数定义

  • 近似算法