算法设计与分析.08.NP 完全性理论 (3)

NP 完全性理论 (3)

• intractability

P与NP

P问题

• 判定性问题（decision problem）

• 算法 \(A\) 是多项式时间的，\(A(s)\) 能够在小于等于 \(p(\vert{s}\vert)\) 步骤内完成
  • \(p(\cdot)\) 是多项式
• P 问题：存在多项式算法的判定性问题
• 例子（质数）

NP问题

• certifier：验证器
• 算法 \(C(t,s)\) 是问题 \(X\) 的验证器
  • \(\forall s\in X\Leftrightarrow \exist t\) 使得 \(C(s,t)=\text{yes}\)
• NP 问题：存在多项式时间验证器的判定算法
  • \(C(t,s)\) 是多项式时间算法
  • \(t\) 是多项式时间的大小，\(\vert{t}\vert\le p(\vert{s}\vert)\)，\(p(\cdot)\) 是多项式
• 多项式是时间可验证的，如果存在一个解，那么是多项式时间可验证的
• 例子（质数）

• SAT \(\in\) NP，3-SAT \(\in\) NP
  • 代入判定即可

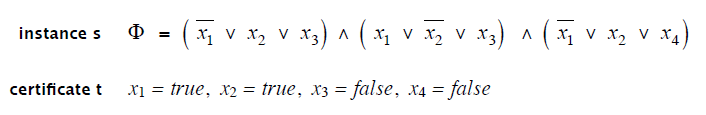
• 哈密顿回路 \(\in\) NP
• NP：Nondeterministic polynomial time
  • 非确定性的，多项式时间可验证的算法
  • 如果找到证据 \(t\)，则就可以在多项式时间验证
  • 但是找到 \(t\) 的时间不确定

P-NP-EXP

• P：Decision problems for which there exists a poly-time algorithm.
• NP：Decision problems for which there exists a poly-time certifier.
• EXP：Decision problems for which there exists an exponential-time algorithm.

关系

• P \(\subseteq\) NP
  • \(C(s,t)=A(s)\) 即可
  • \(A(s)\) 是多项式时间的算法
• NP \(\subseteq\) EXP
  • \(\vert{t}\vert\le p(s)\)
  • 枚举所有的 \(t\)，每一个 \(t\) 可以在多项式时间内验证
  • 如果有一个 \(t\) 返回 yes，则返回 yes
• 3-SAT \(\in\) EXP
  • 枚举 \(2^n\) 种赋值
• 推测（conjecture）：3-SAT \(\notin\) NP

P=NP?

• 一般观点：no

NPC

• NP complete

多项式归约

• Cook 归约：多次调用
  • 多项式时间归约
  • polynomial (Cook) reduction
• Karp 归约：一次调用
  • 多项式时间变换
  • polynomial (Karp) transformation

• 在描述中，我们混用他们，因为在问题的难易程度上，都表示 X 不比 Y 难

NPC

• NP complete
• \(Y\in NPC\)
  • \(Y\in NP\)
  • \(\forall X\in NP,X\le_{p} Y\)
• 如果 \(Y \in NPC\)，此时 \(Y\in P\Leftrightarrow P=NP\)
  • \(\Rightarrow\)：

\[ \begin{array}{c} \forall X\in NP,X\le_{p}Y\Rightarrow X\in P\\ NP\subseteq P \end{array} \]

• 第一个被证明的 NPC 问题
• SAT \(\in\) NPC

证明 NPC

• 如何证明 \(Y\in NPC\)
  • \(Y\in NP\)
  • 找到 \(X\in NPC\)
  • 证明 \(X\le_{p} Y\)
• 传递性

NPC 问题

• Cook-Levin / Karp

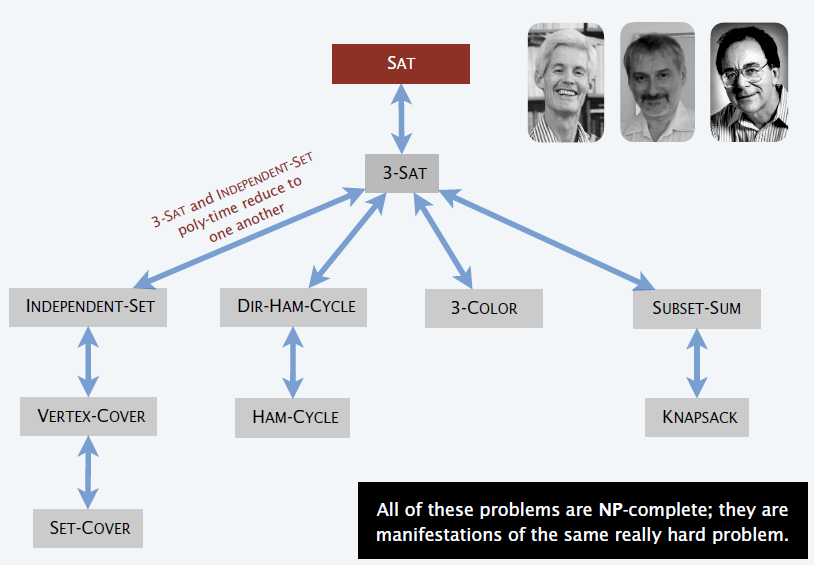
• 《Computers and Intractability》
  • Garey and Johnson

co-NP

• NP 问题的补问题
• Set / Un-Set
  • Set：判定一个 CNF 可满足
  • Un-Set：判定一个 CNF 不可满足
• 哈密顿回路 / 不存在哈密顿回路
• Set \(\in\) NPC，Set \(\equiv_{p}\) Un-Set，但是 Un-Set \(\notin\) NP
  • 不是多项式时间可验证的
• 问题 \(X\) 的补问题 \(\overline{X}\)：和 \(X\) 相同，只是把回答互换了（yes/no 互换）
• co-NP：NP 问题的补问题
• NP=co-NP ?
  • 一般认为：no

定理

\[ NP\ne co-NP\Rightarrow P\ne NP \]

• P 问题的补问题还是 P 问题
• 如果 \(P=NP\)，那么 NP 问题的补问题还是 NP 的，于是 \(NP=co-NP\)

NP-coNP

• 二部图的匹配问题
• 给定一个二部图，问是否存在完美匹配？
  • yes：存在匹配
  • no：存在一个节点子集 S，满足 \(\vert\text{neighbor}(S)\vert\le\vert{S}\vert\)
• 最大流——最小割
  • 最大流 \(\ge k\) ？（NP）
  • 最大流 \(\le k-1\)？（co-NP）
    • 最小割 \(\le k-1\) （NP）
• 好的形式化能够让问题变简单
• 观察

\[ P\subseteq NP\cap co-NP \]

• \(P=NP\cap co-NP\) ？
  • 没有统一意见

Linear programming

• 线性规划问题

\[ A\in\mathrm{R}^{m\times n},b\in\mathrm{R}^{m},c\in\mathrm{R}^{n},\alpha\in\mathrm{R} \]

• 是否存在 \(x\in\mathrm{R}^{n}\) 满足 \(Ax\le 0,x\ge 0,c^{T}x\ge\alpha\)
• 补问题
  • 如果有解，则 max=min

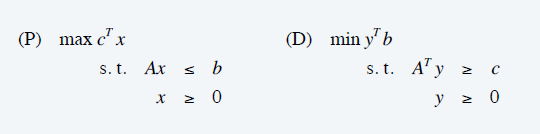
• 线性规划 \(\in NP \cap co-NP\)
  • [Gale–Kuhn–Tucker 1948]
• 线性规划 \(\in P\)
  • [Khachiyan 1979]

Primes

• primes \(\in NP\cap co-NP\)
  • [Pratt 1975]

• primes \(\in P\)
  • [Agrawal–Kayal–Saxena 2004]

质因子分解

• factorize：给定 x，找到 x 的质因数分解
• factor：给定 x、y，问 x 是否存在比 y 小的因数（非1）
• factor \(\equiv_{p}\) factorize
  • \(\le_{p}\)：找到因子分解，然后逐个过一遍就好
  • \(\ge_{p}\)：二分找到因子，除以这个因子继续重复这个步骤
• factor \(\in NP\cap co-NP\)
  • certificate：给定一个小于 \(y\) 的因子
  • disqualifier：给定质因数分解（都小于 \(y\)）
• factor \(\in\) P ？
  • 暂时未知
• RSA 加密算法：利用质数相乘容易，之因素分解难的性质
• 量子计算机：\(n\) bit 整数能够在 \(O(n^3)\) 时间按复杂度上计算
  • 引入了随机
  • 有一定错误概率
• P = BQP ?
  • BQP：bounded error quantum polynomial time

NP 难

• NP-complete（NP 完全）
  • A problem in NP such that every problem in NP poly-time reduces to it.
• NP-hard（NP 难）
  • A problem such that every problem in NP poly-time reduces to it.
  • 和 NPC 相比，不要求问题本身是 NP 的