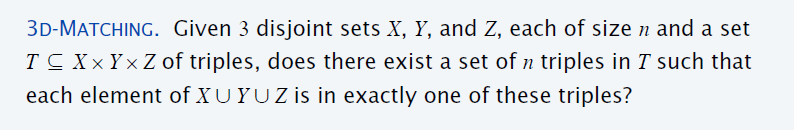算法设计与分析.08.NP 完全性理论 (2)

Posted on Edited on In Views:
划分问题，图着色问题，数值问题（子集和问题，背包问题）

NP 完全性理论 (2)

  • intractability

划分问题

  • partitioning problems

3d匹配

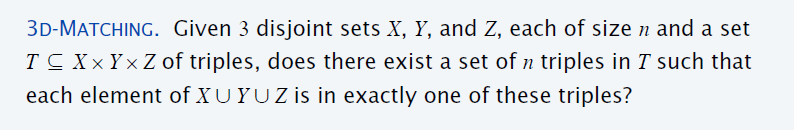
实例

  • \(n\) 个老师，\(n\) 门课，\(n\) 个时间段
  • 给定一些三元组 \((t_i,c_j,t_k)\)，表示老师 \(t_i\) 可以在 \(t_k\) 时间教课程 \(c_j\)
  • 能否找到一个所有老师、课、时间正常不冲突的安排

3SAT-3d匹配规约

  • 3-SAT \(\le_{p}\) 3d 匹配规约

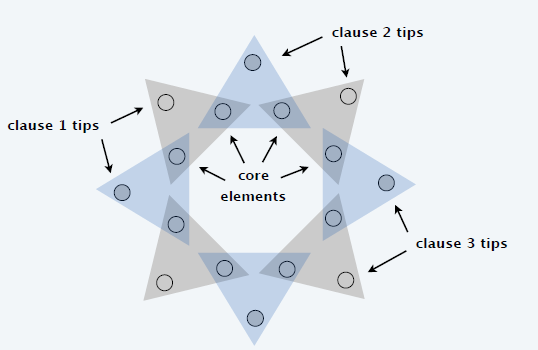
构造

  • \(n\) 个变量，\(k\) 个子句
灰色蓝色
  • 每一个变量构建一个 gadget
    • \(2k\) 个三角形
    • 灰色：\(x_i\) 赋值 true
    • 蓝色：\(x_i\) 赋值 false
  • 每一个三角形表示一个匹配
    • 保证了每一个完美匹配使用了 \(C_i\) 中所有蓝色/灰色块
  • \(k=3\)

绿色
  • 每一个 \(C_i\) 增加一个 gadget，两个元素和每一个文字对应的 gadget 中对应的 tip 连线
  • \(C_1=x_1\lor \overline{x_2}\lor x_3\)
    • \(C_1\) 中的两个元素和 \(x_1\) gadget 中的对应子句 \(C_1\) 的 \(x_1\)（false）tip 相连
      • 如果 \(x_1\) = true，此时选择了灰色的三角形，于是蓝色的空下来了，\(C_1\) 连蓝色的，赋值为真
    • \(C_1\) 中的两个元素和 \(x_2\) gadget 中的对应子句 \(C_1\) 的 \(x_2\)（true）tip 相连
    • \(C_1\) 中的两个元素和 \(x_3\) gadget 中的对应子句 \(C_1\) 的 \(x_3\)（false）tip 相连

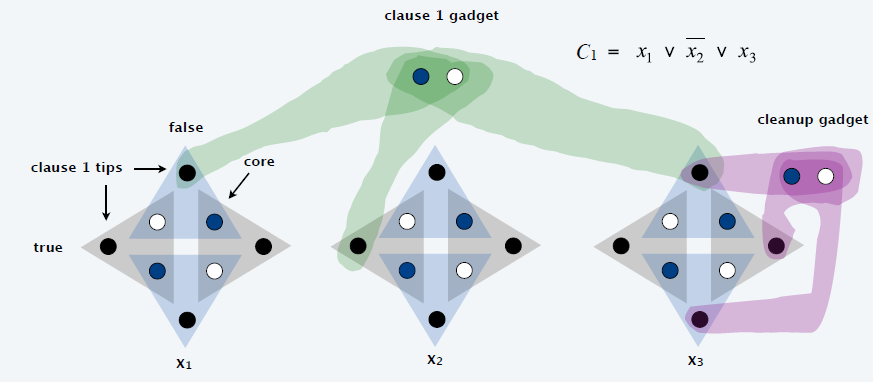
紫色
  • tips 有多出来
  • tips：\(2nk\)
  • 匹配
    • 蓝/灰：\(nk\)
    • 绿：\(k\)
  • 不是完美匹配
  • 添加边，添加 \((n-1)k\) 个 clean gadget
    • 每一个 clean gadget 和所有的 tips 相连
    • 例如上面的紫色，这个 clean gadget 应该有 12 条边，上面只是和 3 个 tips 相连，应该和所有的（12 个）tips 相连

证明

  • \(\Rightarrow\)：蓝/灰色根据变元取值，绿色任意取一个，紫色选择剩下的
  • \(\Leftarrow\)：\(x_i\) 按照是蓝色还是灰色进行赋值
    • 每一个变元选择的三角形都是蓝色或者灰色

图着色问题

  • 3色问题
    • 给定一个无向图，能够使用 3 种颜色对顶点进行一个着色，使其满足任意一条变得两个顶点颜色不同
  • 2着色问题 \(\Leftrightarrow\) 判断是不是二部图 \(\Leftrightarrow\) 判断是否存在奇回路
    • BFS
  • 寄存器分配问题
  • 3 着色问题 \(\le_{p}\) 寄存器分配问题（\(k\ge3\)）

3色问题

  • 3-SAT \(\le_{p}\) 3 着色问题

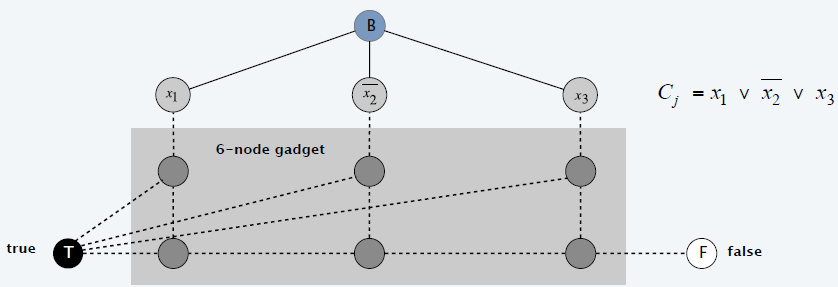
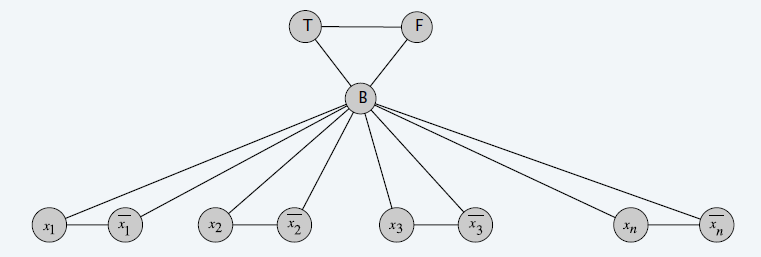
构造

  • 每个文字一个节点
    • \(x_i,\overline{x_i}\) 之间加一条边
  • 3 个节点：T、B、F
    • 所有文字和 B 之间连一条边
  • 每一个子句一个 gadget
    • 6节点，13边

证明

充分性
  • \(\Rightarrow\)
  • 假设：T 黑色，F 白色，B 蓝色
  • 着色为黑色为 true，白色 false
    • 这需要保证所有的文字都被着色为i黑色或者白色（B 相连保证）
    • \(x_i\) 和 \(\overline{x_i}\) 着色不同（\(x_i,\overline{x_i}\) 相连保证）
    • 需要保证子句 \(C_i\) 中的任意一个文字为 true（着色为黑色）
      • badget 保证
  • badget
    • 假设全白，则无法 3 着色

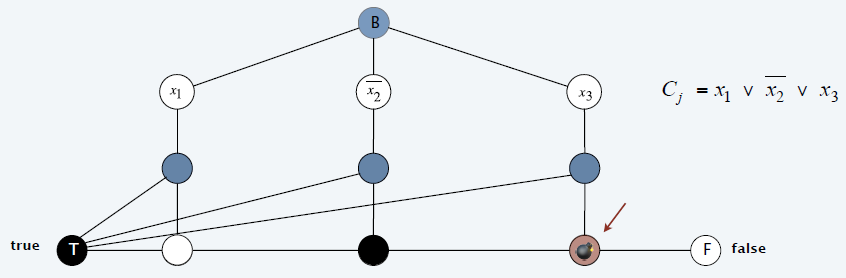
必要性
  • \(\Leftarrow\)
  • 其他显然，枚举证明1，2，3个黑色，badget 都能 3 着色即可

数值问题

  • 子集和问题
  • 给定 \(n\) 个自然数的集合 \(S\) 和一个整数 \(W\)，能否找到 \(S\) 的一个子集，然集合元素和恰好为 \(W\)

子集和问题

  • 3-SAT \(\le_{p}\) 子集和问题
  • \(n\) 个语句，\(k\) 个子句

构造

  • \((2n+2k)\) 个 \((n+k)\) 位十进制整数
  • \(n\) 位：\(x_i\)，\(k\) 位：\(C_j\)
  • 每一个文字一行，\(y=x_i/\overline{x_i}\) 行
    • 高位：\(y=x_k\lor \overline{y}=x_k\)，则为 1
    • 低位：\(y\in C_k\)，则为 1
  • 每个子句一行，\(y=C_i\)
    • 两行：\(y=C_k\Rightarrow \{1,2\}\)
  • \(W\)：高位1，低位4

  • 注意不管怎么选都不会有进位

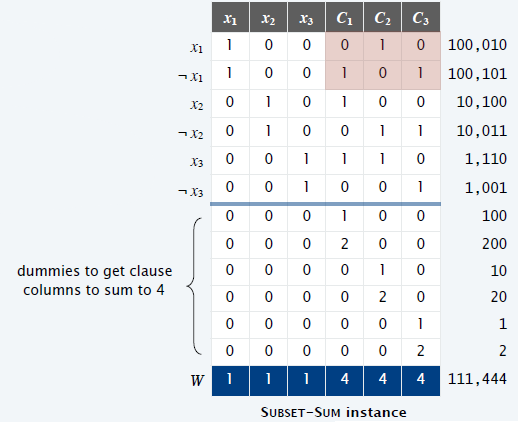
证明

  • \(\Rightarrow\)
    • \(x_i\) 为真则选择 \(x_i\) 行，否则选 \(\overline{x_i}\)
    • 此时 \(C_j\) 列至少为 1，选择 \(C_j\) 对应的数可以得到 4
      • 1 选择 1,2
      • 2 选择 2
      • 3 选择 1
  • \(\Leftarrow\)：赋值即可
    • \(x_i,\overline{x_i}\) 有且只会选中一个
    • \(C_j\) 列至少为 1

背包问题

  • knapsack
  • 物品重量 \(w_i\)，价值 \(v_i\)，选中若干物品，重量和小于等于 \(W\)，价值和大于等于 \(U\)
  • dp：\(O(nU)\)
  • 子集和问题 \(\le_{p}\) 背包问题
  • 构造，子集和问题是背包问题的子问题
    • \(W=U\)
    • \(v_i=w_i,\forall i\)

总结