算法设计与分析.08.NP 完全性理论 (1)

Posted on Edited on In Views:
NP 完全性理论，多项式时间归约，覆盖问题，约束满足问题，等价转化（判定问题，搜索问题，最优化问题），排列问题（哈密顿回路）

NP 完全性理论

  • intractability

多项式时间规约

  • poly-time reductions
  • 实际可求解的问题：多项式算法类（poly-time algorithm）
  • 是否可以多项式求解 | yes | probably no | | :----: | :----: | | shortest path | longest path | | min cut | max cut | | 2-satisfiability | 3-satisfiability | | planar 4-colorability | planar 3-colorability | | bipartite vertex cover | vertex cover | | matching | 3d-matching | | primality testing | factoring | | linear programming | integer linear programming |

指数级算法

  • 已被证明
  • k-停机问题：Given a constant-size program, does it halt in at most k steps?
  • 棋盘必胜策略：Given a board position in an n-by-n generalization of checkers, can black guarantee a win?
  • 问题分类（指数/多项式），这本身也不容易

多项式时间规约

  • \(X\le_{P}Y\)
  • 问题 \(X\) 多项式时间（Cook）归约到问题 \(Y\)
    • 如果对于 \(X\) 问题的任意一个实例能够通过以下方式求解
      • 多项式次数调用解决问题 \(Y\) 的算法
      • 多项式时间的额外的计算步骤

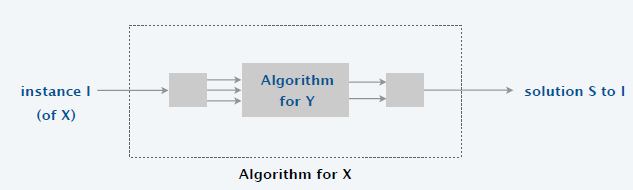
  • 理解：\(X\) 的难度比 \(Y\) 小
    • 如果问题 \(Y\) 能在多项式时间内求解，那么问题 \(X\) 也能在多项式时间内求解
    • 如果问题 \(X\) 不能在多项式时间内求解，那么问题 \(Y\) 也能在多项式时间内求解
  • \(X\equiv_{p}Y\)：\(X\le_{P}Y\land Y\le_{P}X\)
  • 传递性

\[ X\le_{P}Y\land Y\le_{P}Z\Rightarrow X\le_{P}Z \]

覆盖问题

  • packing and covering problems

独立集

  • Independent set
  • 给定图 \(G=(V,E)\) 和整数 \(k\)，问是否至少存在这样的点集
    • 点数不超过 \(k\) ，这些点互不相邻

点覆盖

  • Vertex cover
  • 给定图 \(G=(V,E)\) 和整数 \(k\)，问是否最多存在这样的点集
    • 点数不超过 \(k\) ，这些点关联所有边

独立集点-覆盖规约

  • 独立集 \(\equiv_{p}\) 点覆盖
  • \(S\) 是 \(k\) 大小的独立集 \(\Leftrightarrow\) \(V-S\) 是 \(n-k\) 的点覆盖

集合覆盖

  • set cover
  • 给定集合 \(U\)，\(U\) 的子集的集合 \(S\)，是否存在 \(S\) 的子集，满足
    • 元素个数小于等于 \(k\)
    • 元素的并等于 \(U\)
  • 应用：很多废旧电脑组装一台新电脑

点覆盖-集合覆盖规约

  • 点覆盖 \(\le_{p}\) 集合覆盖
  • 证明思路
    • 对于点覆盖问题的一个实例 \(G=(V,E)\) 和参数 \(k\)，构造一个集合覆盖问题 \((U,S,k)\)
    • 证明：\(G\) 有一个大小为 \(k\) 的点覆盖 \(\Leftrightarrow\) \((U,S,k)\) 有大小为 \(k\) 的集合覆盖

构造

  • \(U=E\)
  • 对每一个节点 \(v\in V\)，构造一个 \(S\) 中的元素 \(S_v\)，\(S_v\) 是 \(v\) 关联的边的集合

证明

  • \(\Rightarrow\)：点覆盖的有解实例能够被正确解决
    • 点覆盖有解，则集合覆盖有解
  • \(\Leftarrow\)：点覆盖的无解实例能够被正确解决
    • 点覆盖无解，则集合覆盖无解
    • \(\Leftrightarrow\) 集合覆盖无解，则点覆盖无解

约束满足问题

  • constraint satisfaction problems
  • 文字：\(x_i,\overline{x_i}\)
    • 变元及其否定形式
  • 子句（Clause）：文字的或
    • disjunction
  • CNF 合取范式：子句的与
    • Conjunctive normal form
  • SAT：给定 CNF 的形式 \(\Phi\)，问是否存在一个使其为真的变元赋值
  • 3-SAT：每一个子句都只有 3 个文字
  • 假设：3-SET 问题没有多项式时间求解的算法
    • 等价于 P \(\ne\) NP

3SAT-独立集规约

  • 3-SAT \(\le_{p}\) 独立集
  • 证明思路：构造+等价
  • 3-SAT：\(k\) 个子句
  • \(G\) 的顶点：\(3k\)
    • 每个子句 3 个节点，每个文字一个节点
  • \(G\) 的边
    • 一个子句中的文字两两相连
    • 每个变元和他的否定形式相连
  • 示例

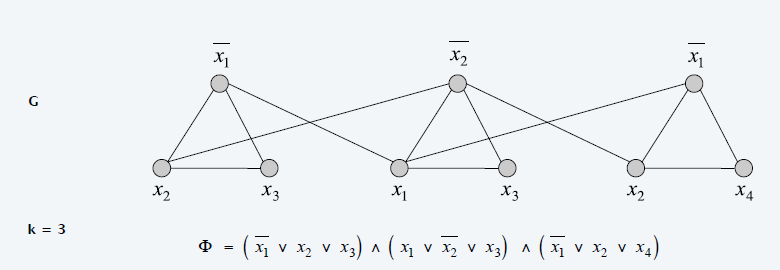
证明

  • 3-SAT 可满足 \(\Leftrightarrow\) 构造的图有 \(k=\vert\Phi\vert\) 独立集
  • \(\Rightarrow\)：
    • 每个子句中选择一个为真的文字，这些文字对应的点的集合就是独立集
  • \(\Leftarrow\)：
    • \(k\) 独立集存在，则肯定是每个子句一个（内部都相连），独立集中的点赋值为真
    • 不会出问题，独立集保证不会出现 \(x_i=\overline{x_i}=true\)（有边）

3 种问题

  • Decision problem（判定问题）
    • Ex：Does there exist a vertex cover of size \(\le\) k?
  • Search problem（搜索问题）
    • Ex：Find a vertex cover of size \(\le\) k.
  • Optimization problem（最优化问题）
    • Ex：Find a vertex cover of minimum size.
  • 3 个问题可以在互相实现多项式时间规约

点覆盖

  • 判定问题：是否存在大小小于等于 \(k\) 的点覆盖
  • 搜索问题：找到大小小于等于 \(k\) 的点覆盖
  • 优化问题：找到大小最小的点覆盖

判定问题搜索问题规约

  • 判定问题 \(\equiv_{p}\) 搜索问题
  • \(\le_{p}\)：判定问题是搜索问题的特例
  • \(\ge_{p}\)：算法如下
    • 判定是否存在大小小于等于 \(k\) 的点覆盖，若不存在则结束，若存在继续
    • 找到一个节点 \(v\) 满足 \(G-\{v\}\) 存在大小小于等于 \(k-1\) 的点覆盖
      • \(k\) 次判定
    • 将 \(v\) 加入点覆盖集合，在 \(G-\{v\}\) 中递归找大小等于 \(k-1\) 的点覆盖

搜索问题优化问题规约

  • 搜索问题 \(\equiv_{p}\) 优化问题
  • \(\le_{p}\)：搜索问题是优化问题的特例
  • \(\ge_{p}\)
    • 二分 \(k\)，得到 \(k^{\ast}\)，找到大小小于等于 \(k^{\ast}\) 的点覆盖
      • \(\log k\) 次调用

sequencing problems

  • 排列中的问题

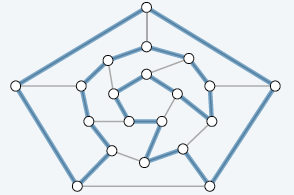
哈密顿回路

  • 无向图 \(G=(V,E)\) 的一条回路，恰好包含所有顶点一次

有向哈密顿回路

  • 有向哈密顿回路 \(\le_{p}\) 哈密顿回路
  • 证明思路：构造+等价
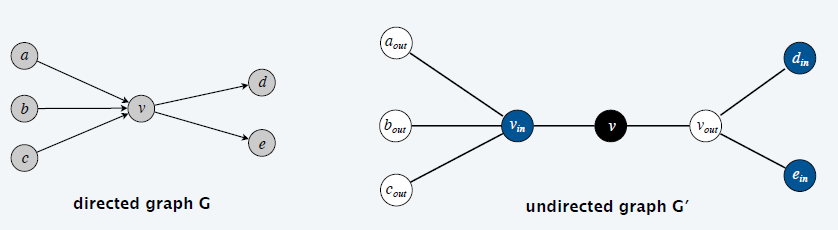
  • 构造：3n 个点
    • 将有向图 \(G\) 的每一个顶点 \(v\) 拆分为 3 个顶点 \(v_{in},v,v_{out}\)
    • \(v\) 和 \(v_{in},v_{out}\) 相连
    • \(e(x,y)\in G\)，则在 \(G'\) 中加入边 \((x_{out},y_{in})\)
  • \(G'\) 中哈密顿回路结构：\(v_i,v_{i,out},v_{j,in},v_j\)
    • \(v_{i,out},v_{j,in}\) 后面肯定得接 \(v_j\)，否则到达 \(v_j\) 肯定是最后一个点，此时无法成环
    • out, in 规定了方向

3SAT-哈密顿回路归约

  • 3-SAT \(\le_{p}\) 哈密顿回路
  • 证明：构造+等价

构造

  • \(n\) 个变元，\(k\) 个子句
    • 构造一个含有 \(2^n\) 个哈密顿回路的图 \(G\)，使得每一个回路对应一个变元的取值
    • 如果 \(x_i\) 行是左到右，则表示 \(x_i\) 赋值 true，否则 false

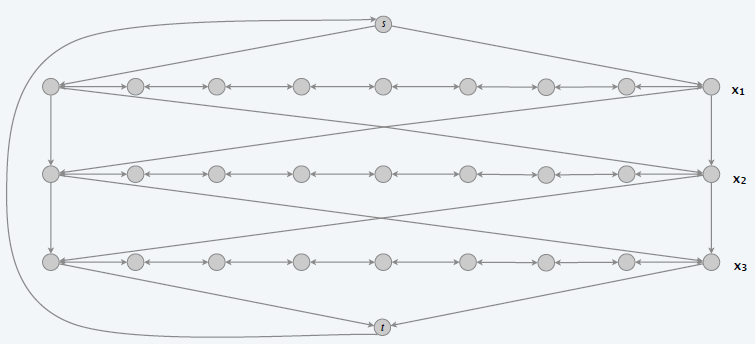
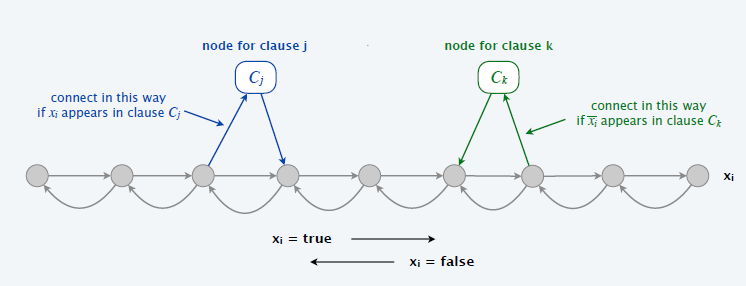
  • 对于每一个子句，增加 1 个节点 \(C_j\)，6 条边
    • 如果 \(x_i/\overline{x_i}\) 出现在 \(C_j\) 中，则 \(C_j\) 和 \(x_i\) 行连边
      • 如果是 \(x_i\)，则左向右连
      • 如果是 \(\overline{x_i}\)，则右向左连
    • 不同的子句节点不能连向同一个点

证明

  • \(\Rightarrow\)：赋值对应的哈密顿回路，串上子句节点
  • \(\Leftarrow\)：
    • \(x_i\) 行指向 \(C_j\)，则必然指回去 \(x_i\) 行
    • 否则 \(C_j\to x_i\) 的那个节点将成为最后一个节点，无法形成回路
    • 这也保证了一行内必然是同向
    • 赋值方式和之前相同