算法设计与分析.07.网络流 (4)
网络流 (4)
- Network Flow
最小代价匹配
- 输入:带权的完全二部图 \(G=(X\cup Y,E)\),\(\vert{X}\vert=\vert{Y}\vert\)
- 输出:最小权重的完美匹配
实例问题
研讨会
- \(m\) 个研讨会,\(n=12m\) 个学生,每个研讨会需要 12 个学生参加
- 每个学生给出一个他最喜欢的研讨会列表(8 个)
- 建模
- \(X\):研讨会(每个研讨会复制 12 份)
- \(Y\):学生
- \(E\):\(X\to Y\) 所有边,权重设置如下
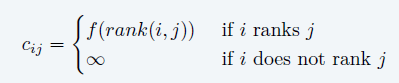
定位
- 通过两个传感器定位场景中 \(n\)
个物体的位置
- 传感器返回一个方向
- 建模
- \(X_i\):传感器 1 对物体 \(i\) 的定位方向
- \(Y_i\):传感器 2 对物体 \(i\) 的定位方向
- \(E_{i,j}\):传感器 1 和物体 \(i\) 的连线、传感器 2 和物体 \(j\) 的连线的距离
- 由于测量误差,\(w(e_{i,j})>0\)
肾脏交换
- 情况
- \(x_i\) 的朋友 \(y_i\) 愿意捐献给 \(x_i\),但是配型很差
- \(x_j\) 的朋友 \(y_j\) 愿意捐献给 \(x_j\),但是配型很差
- \(x_i-y_j,x_j-y_i\) 配型好
- 边权设置:配型越好越小,配型越差越大
二部图匹配
- \(w(e)=1,\forall e\in E\)
- 规约为最大流
- 0-1 流
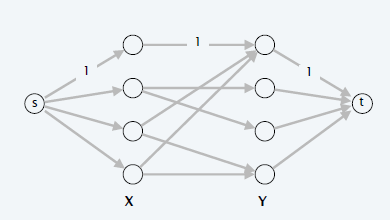
- 残差图 \(G_M\) 如下
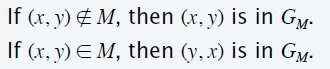
- 增流路径
- 起始边:\(s\to x\),\(x\in X\) 是非匹配点
- 中间边:匹配边和非匹配边的交错路径
- 终止边:\(y\to t\),\(y\in Y\) 是非匹配点
交错路径
- 上面的增流路径的中间边
- 匹配边和非匹配边的交错路径
- 如果匹配 \(M\) 存在交错路径 \(P\),则 \(M'=M\oplus P\) 也是一个匹配,而且 \(\vert{M'}\vert=\vert{M}\vert+1\)
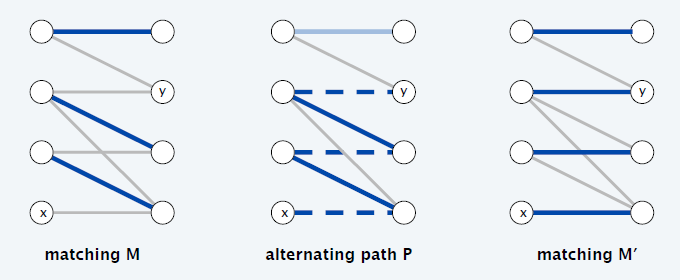
- 代价(cost):\(P\) 上关于匹配
\(M\) 的非匹配边权重之和 -
匹配边权重之和
- to match - to unmatch
- 最短交错路径:cost 最小的交错路径
successive shortest path algorithm
- 解决最小代价匹配问题
- 算法:从空匹配开始,反复寻找最短交错路径,直到找不到
- 如何找到最短交错路径?
- \(s\to t\) 的最短路
- 找最短路时,边的方向如下(和 \(G_M\) 的定义一致)
- 匹配边:\(X\to Y\)
- 非匹配边:\(Y\to X\)
- 最短路是交错路径
- \(s\) 的下一个点一定是 \(X\) 中未匹配的点
- 路径中的点 \(y\in Y\) 的下一个点
\(y'\) 一定是 \(X\) 中的匹配点或者 \(t\)
- 否则 \(G_M\) 中不存在边 \(y'\to y\),同样转换图中也不存在
- 路径中的点 \(x\in X\) 的下一个点
\(x\) 一定是 \(Y\) 中的匹配点
- 转换图中匹配边权值为 0(后面证明)
- Dijkstra 算法
- 负权边如何处理?
- 如果没有负权环,使用 Bellman-Ford 算法
- 进行转换,把负权边转化为非负权边
等价转换
- 对于 \(\forall x\in X\),将它的所有出边都加上/减去 \(p(x)\) 最小代价匹配对应的边不变
- 对于 \(\forall y\in Y\),将它的所有入边都加上/减去 \(p(y)\) 最小代价匹配对应的边不变
- 证明:对于完美匹配 \(M\) 和任意 \(x\in X,y\in Y\),肯定会使用到 \(x\) 中一条出边,\(y\) 的一条入边
转换后的代价函数
- reduced cost:\(c^{p}(x,y)\)
- 从 \(X\) 到 \(Y\)
\[ c^{p}(x,y)=p(x)+c(x,y)-p(y) \]
- Compatible prices:相容赋值
- \(p(x),p(y)\) 满足如下条件
\[ \begin{array}{cc} c^p(x,y)\ge 0,&\text{for all }(x,y)\notin M\\ c^p(x,y)= 0,&\text{for all }(x,y)\in M\\ \end{array} \]
- 如果代价函数是相容赋值,而且 \(M\)
是完美匹配,那么 \(M\) 是最小代价匹配
- 证明:\(cost(M)=0\)
算法

引理1
- \(p\) 是相容赋值,\(d\) 是 \(G_M\) 关于 \(c^p\) 的最短路,那么 \(d\) 上的边都满足 \(c^{p+d}(x,y)=0\)
- 证明
- 对于 \((x,y)\in d\) 都有 \(d(x)+c^{p}(x,y)-d(y)=0\)
- \((x,y)\in M\)
- 于是有 \((y,x)\in d\)
- 于是有 \(d(x)=d(y)-c^{p}(x,y)\)
- \((x,y)\notin M\)
- 于是有 \((x,y)\in d\)
- 于是有 \(d(y)=d(x)+c^{p}(x,y)\)
- 根据定义
\[ c^{p}(x,y)=p(x)+c(x,y)-p(y) \]
- 于是有
\[ \begin{aligned} c^{p+d}(x,y) &=\Big(p(x)+d(x)\Big)+c(x,y)-\Big(p(y)+d(y)\Big)\\ &=p(x)+c(x,y)-p(y)-c^{p}(x,y)\\ &=0\\ \end{aligned} \]
- 证毕
- 这里匹配边赋值为 0,保证了在下一步找最短路时,可以将匹配边定义为反向
- \(G_M\) 的合理性(即这里说明了为什么定义 \(c^{p}(x,y)\) 的时候说 \(X\to Y\),但是在找最短路的时候匹配边是 \(Y\to X\) 的)
引理2
- \(p\) 是相容赋值,\(d\) 是 \(G_M\) 关于 \(c^p\) 的最短路,那么 \(p'=p+d\) 也是相容赋值
- 证明:分类
- \((x,y)\in M\)
- \((y,x)\) 是图 \(G_M\) 中唯一的一条 \(x\) 的入边
- 对于未匹配边,流量为 0,在残差图中没有反向边
- 因此 \((x,y)\in M\)
- 根据引理 1,\(c^{p+d}(x,y)=0\)
- \((y,x)\) 是图 \(G_M\) 中唯一的一条 \(x\) 的入边
- \((x,y)\notin M\)
- 对于未匹配边,流量为 0,在残差图中有正向边(而且是 \(X\to Y\) 的边)
- 距离三角不等式:\(d(y)\le d(x)+c^{p}(x,y)\)
\[ \begin{aligned} c^{p+d}(x,y) &=\Big(p(x)+d(x)\Big)+c(x,y)-\Big(p(y)+d(y)\Big)\\ &=\Big(p(x)+c(x,y)-p(y)\Big)+\Big(d(x)+d(y)\Big)\\ &=c^{p}(x,y)+\Big(d(x)-d(y)\Big)\\ &\ge0\\ \end{aligned} \]
引理3
- \(p\) 是 \(M\) 的相容赋值,\(M'\) 是 \(M\) 按照最短路 \(d\) 增流之后的匹配,则 \(p'=p+d\) 是 \(M'\) 的相容赋值
- 证明
- 引理2 \(\Rightarrow\) \(p'\) 是 \(M\) 的相容赋值
- 相较于 \(M\) 而言,\(M'\) 只是把 \(d\) 上的边进行反向了
- 由引理1,\(d\) 上的边满足 \(c^{p+d}(x,y)=0\)
- \(c^{p+d}(x,y)\) 和方向性无关,都是从 \(X\to Y\)
- 证毕
算法正确性
- 初始 \(p\) 相容,根据引理 2、3,算法一直都是相容的,在找到完美匹配的时候,\(w(M)=0\),是最小权值匹配
算法复杂度
- \(O(n^3)\)
- \(n\) 次迭代(找最短路)
- Dijkstra 算法:\(O(n^2)\)
- \(m=n^2/4\)
发展

Input-queued switching
- 数据包要从 \(x_i\to y_j\)
- 一个时间片内,一个 \(x_i\) 只能发送一个包,一个 \(y_i\) 只能接收一个包
- 如果两个数据包,起点终点都不冲突,可以一起发送
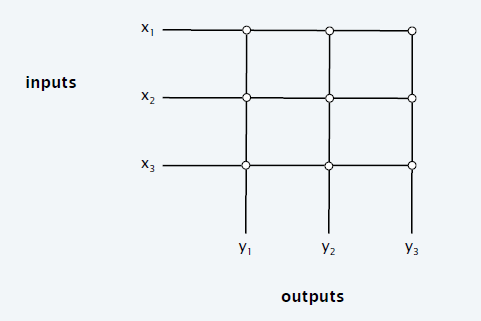
FIFO
- 问题:Head-of-line blocking (HOL)
- 这个时刻本来可以发送:\((x_1\to y_1,x_2\to y_2,x_3\to y_3)\)
- 但是由于 FIFO,最多只能发送两个包
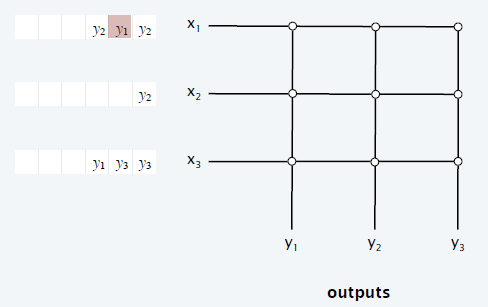
- uniform i.i.d.:58% throughput
VOQ
- Virtual output queueing
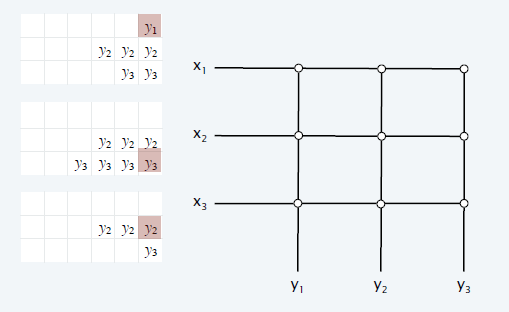
- 每一个输入维护关于每一个输出的队列
- 找最大匹配
- uniform i.i.d.:100% throughput
- 问题:starve input-queues when arrivals are nonuniform
最小带权匹配
- LQF:\(c(x_i,y_j)\) 表示 \(x_i\) 传到 \(y_j\) 的包数量
- OCF:\(c(x_i,y_j)\) 表示 VOQ 算法中距离上一次传送 \(x_i\) 到 \(y_j\) 包的时间
- independent (even if not uniform):100% throughput
- 问题
- 硬件难以实现
- 匹配过慢
- 意义
- 提供了理论框架