算法设计与分析.07.网络流 (3)
网络流 (3)
- Network Flow
bipartite matching
- 图 \(G=(V,E)\) 的一个匹配 \(M\in E\),满足每个节点最多在 \(M\) 中出现一次
- 最大匹配:\(\vert{M}\vert\) 最大的匹配
- 二分图:能够将节点划分为两个部分 \(A,B\),只有 \(A,B\) 之间有边
max-flow
- 转化为 max-flow 问题
- 增加两个虚拟节点 \(s,t\),分别和两个部相连
- 中间的权重设置为 1 也行
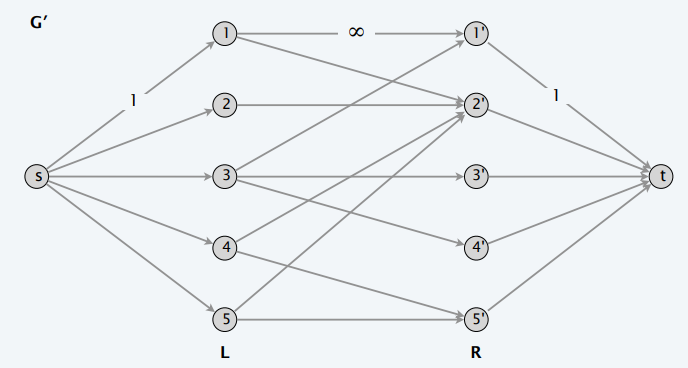
- 匹配 \(M\) 和流量 \(f\) 一一对应
- SB 定理
- 单射 + 单射 = 双射
- \(A\subseteq B\land B\subseteq A\Rightarrow A=B\)
- FF 算法:\(O(mn)\)
完美匹配
- 每个 \(G\) 中的顶点恰好都在 \(M\) 中出现 1 次
- \(S\):节点子集
\[ N(S)=\{v:edge(w,v)\in E\land v\in S\} \]
Hall
- 满足 \(\vert{L}\vert=\vert{R}\vert\) 的二部图
\(G=(V,E)\),\(V=L\cup R\)
- \(G\) 存在完美匹配 \(\Leftrightarrow\) 对于任意 \(S\subseteq L\),都有 \(\vert{N(S)}\vert\ge \vert{S}\vert\)
- 注意 Hall 定理的前提是二部图
- \(\Rightarrow\)
- 每一个点都需要匹配到不一样的点
- \(\Leftarrow\)
- 反证法
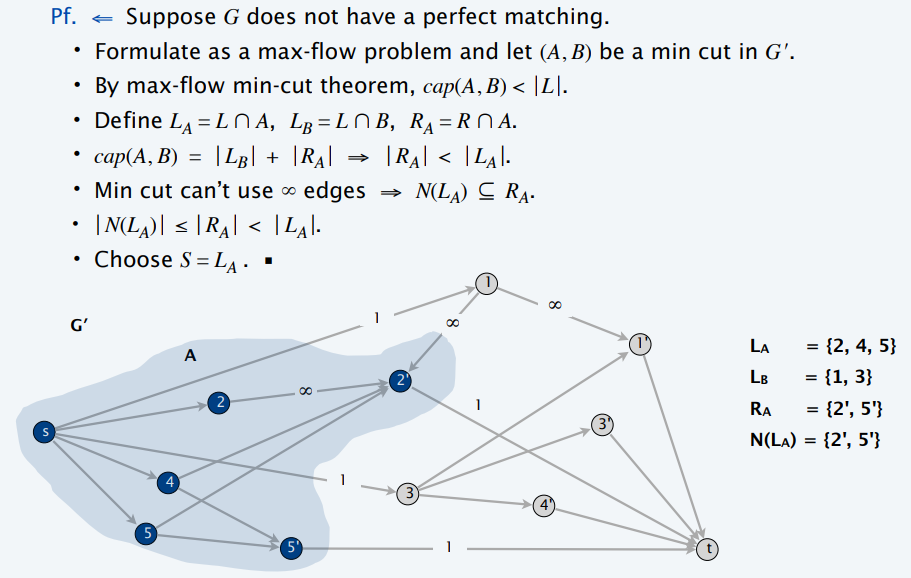
- \(cap(A,B)=\vert{L_B}\vert+\vert{R_A}\vert\)
- 从最小割的角度思考
- 首先不会包含 \(\infty\)
的边,也就是说 \(A\)
只有可能有如下两种情况
- \(A=\{s\}\)
- \(A=\{s\cup V_1\}\),同时 \(V_1\) 和 \(V-V_1\) 之间没有边
- 再观察就看得出来上面的式子了
- \(N(L_A)\subseteq R=R_A\cup
R_B\),\(R\) 除去无穷边(连接
\(L,R\) 的边),即 \(R_B\)
- 于是 \(R_B\) 中的点不在 \(N(L_A)\) 中
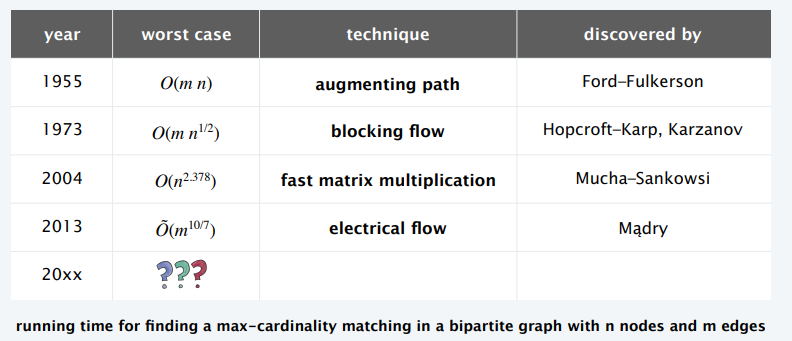
发展史
非二部图的匹配
- 结构更加复杂
- Blossom algorithm:\(O(n^4)\)
- [Edmonds 1965]
- Best known:\(O(mn^{0.5})\)
- [Micali–Vazirani 1980, Vazirani 1994]
k-regular bipartite graph
- 二部图,每个节点恰好都有 \(k\) 个相邻的点
- every k-regular bipartite graph have a perfect matching
- 证明
- 和 \(S\) 关联的边的数量 \(k\vert{S}\vert\)
- 和 \(N(S)\) 关联的边的数量 \(k\vert{N(S)}\vert\)
- 和 \(S\) 关联的边一定和 \(N(S)\) 关联
- \(k\vert{N(S)}\vert\ge k\vert{S}\vert\)
- \(\vert{N(S)}\vert\ge \vert{S}\vert\)
- 根据 Hall,得证
disjoint paths
- edge-disjoint paths:路径两两之间没有相同的边
- 节点可以相同
Edge-disjoint paths problem
- 图 \(G=(V,E)\),给定点 \(s,t\),找出最多的边不相交的路径
- 最大流模型:所有的容量都设置为 \(1\)
- 正确性:证明双射
- 路径 \(\Rightarrow\) 最大流:赋权即可
- 最大流 \(\Rightarrow\) 路径:根据流守恒提取出 k 条路径
Network connectivity
- 有向图删除几条边,才能让 \(s\)
不可达 \(t\)
- 和上面一样的转化,求最小割
Menger’s theorem
- The max number of edge-disjoint \(s\to t\) paths equals the min number of edges whose removal disconnects \(t\) from \(s\)
- 路径 \(P_1,\cdots,P_k\)
- 去除边集 \(\vert{F}\vert=l\)
- \(\le\):每条路径至少使用了 \(F\) 的一条边
- \(\ge\):最大流 \(\Rightarrow\) 最小割 \(\Rightarrow\) \(k\ge l\)
无向图
- 最大流模型:每一条边 \(e(u,v)\) 转化为两条有向边 \(e(u,v),e(v,u)\),权重设置为 1
- 存在最大流,使得对于任意一组反向边 \(e,e'\),满足 \(f(e)=0\lor f(e')=0\)
- 证明
- 若存在不满足条件的边,则都减去 \(\min\{f(e),f(e')\}\),此时 \(val(f')=val(f)\)
- 正确性:证明双射
- 路径 \(\Rightarrow\) 最大流:赋权即可
- 最大流 \(\Rightarrow\) 路径:转化为 \(f(e)=0\lor f(e')=0\),然后再根据流守恒提取
Menger 定理

最大流扩展
多源多汇
- 增加一个虚拟的源点、一个虚拟的汇点
- 虚拟源点连接所有的源点,权重设置为 \(\infty\)
- 接所有的汇点连虚拟汇点,权重设置为 \(\infty\)
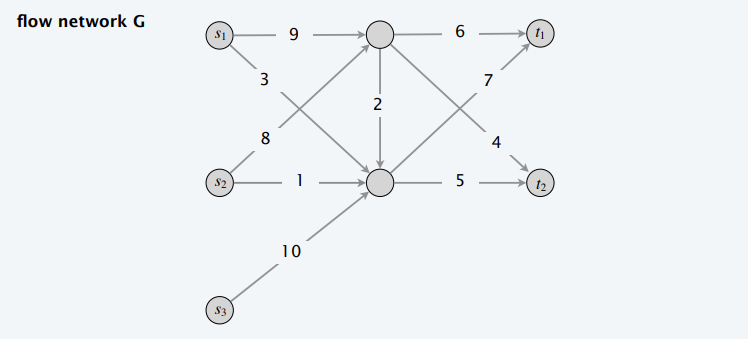
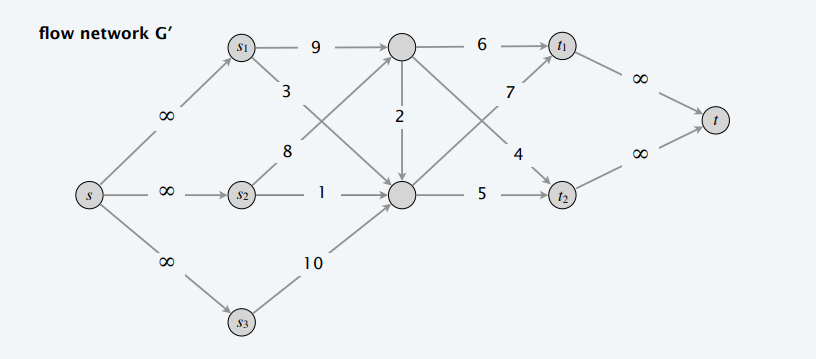
顶点有需求
- Circulation with supplies and demands
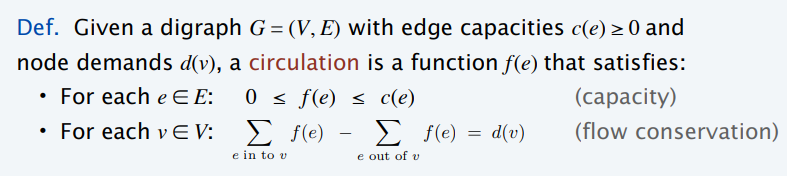
- 看能否构建起流通
- 增加虚拟的源点和汇点,边这么加

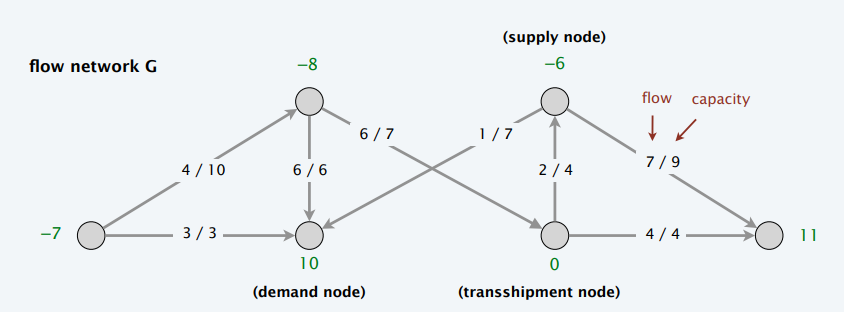
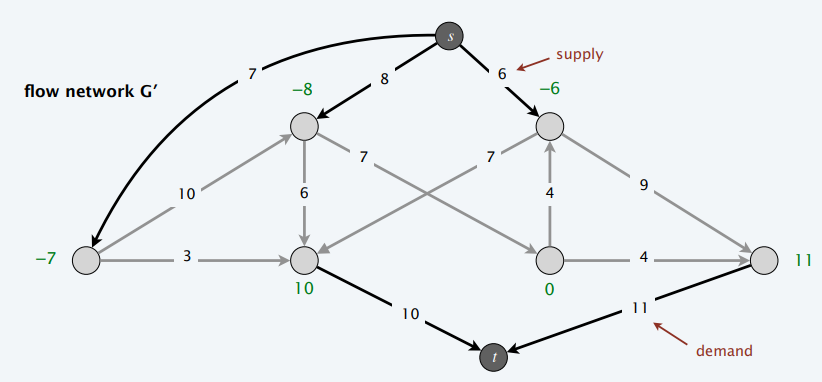
- 能流通起来,当且仅当存在最大流 \(D\)
- 只有把新加的边满起来了,才能满足流量限制
\[ D=\sum_{v:d(v)>0}d(v)=\sum_{v:d(v)<0}-d(v) \]
- \(c(e),d(v)\)
都是整数,如果存在流通,则存在赋值全为整数的循环
- max-flow
- 不存在流通 \(\Leftrightarrow\)
存在一个划分 \((A,B)\),使得 \(\sum_{v\in B}d(v)>cap(A,B)\)
- 需要的超过了能供给的
- 图 \(G'\) 中的割集 \((A,B)\),记作 \(cap'\)
\[ \begin{aligned} cap'(A,B) &=cap(A,B)+\sum_{v\in B\land d(v)<0}-d(v)\\ &<\sum_{v\in B}d(v)+\sum_{v\in B\land d(v)<0}-d(v)\\ &=\sum_{v\in B\land d(v)>0}d(v)\\ &\le\sum_{v\in V\land d(v)>0}d(v)\\ \end{aligned} \]
- 不满足流通条件了
带下界+顶点有需求
- Circulation with supplies, demands, and lower bounds
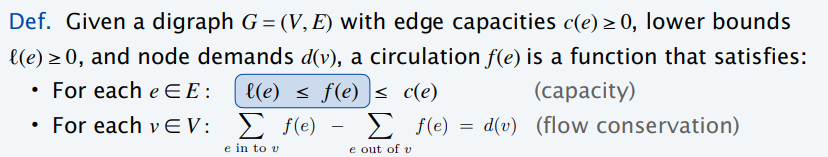
- 把边的下界转换到点上
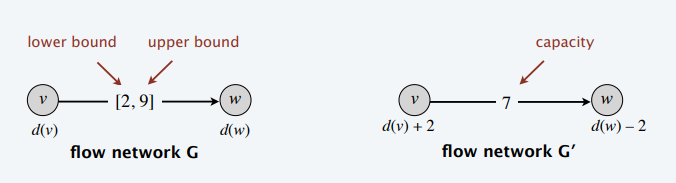
- \(G\) 中有流通 \(f(e)\) \(\Leftrightarrow\) \(G'\) 中有流通 \(f(e)-l(e)\)
应用
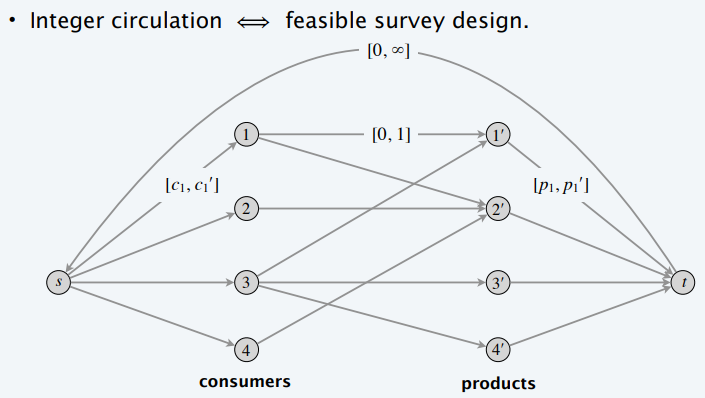
Survey design

- 求一个流通,注意 \(t\to s\) 的边
airline scheduling
- 重用航班人员、飞机,很难的问题

- 不考虑时间,二分求解流通问题

- 时间复杂度:\(O(k^3\log k)\)
- \(k\) 个航班
- edge:\(O(k^2)\)
- node:\(O(k)\)
- \(\log k\) 次尝试
- 每次 \(O(k^3)\),\(O(mn)\)
- \(k\) 个航班
- Can solve in \(O(k^3)\) time by formulating as minimum-flow problem
image segmentation
- 前后景分割
- 无向图
- node:像素
- edge:最多 4 个邻居像素
- \(a_i\):像素为前景的概率
- \(b_i\):像素为后景的概率
- \(p_{i,j}\):penalty 当 \(i,j\) 一个是前景一个是后景
- Goal

- 转化为最小化问题
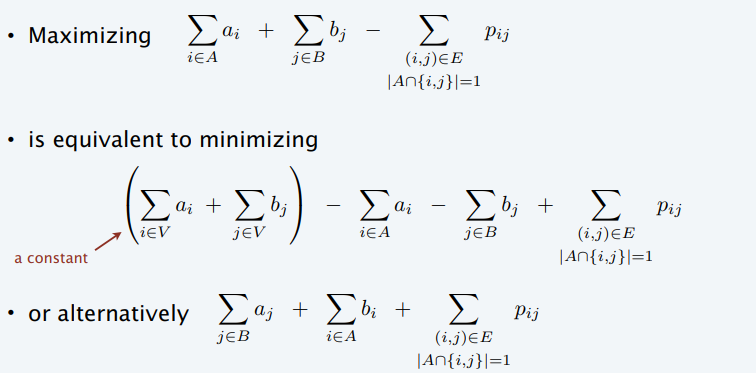
建模
- 无向图转为有向图
- s-j:\(a_j\)
- i-t:\(b_i\)
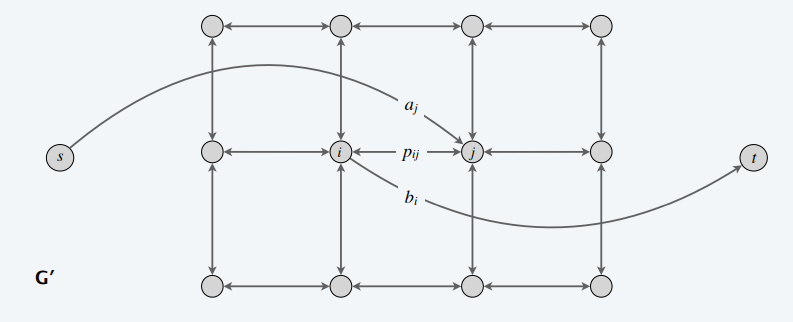
- 转变为最小割问题
- Grabcut. [ Rother–Kolmogorov–Blake 2004 ]
project selection
- 每一个工程需要财政 \(p_v\)(可正可负)
- 若干限制:\(v\) 需要在 \(w\) 之前
- 目标:满足限制条件下,最大化财政
- 先驱图:\(w\) 是 \(v\) 的先决条件 \(\Rightarrow\) edge(v,w)
- 最小割模型

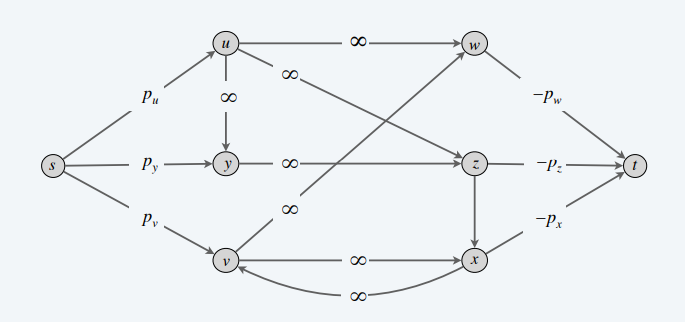
- \((A,B)\) 是最小割 \(\Leftrightarrow\) \(A-\{s\}\) 是最优结果
- 最小割不会选中 \(A\to B\) 的无穷边
- \(A\to B\) 的边
- \(s\to v,v\in B\)
- \(v\to t,v\in A\)
\[ \begin{aligned} cap(A,B) &=\sum_{v\in B:p_v>0}p_v+\sum_{v\in A:p_v<0}(-p_v)\\ &=\sum_{v:p_v>0}p_v-\sum_{v\in A}p_v\\ \end{aligned} \]
- 第一项为常数,第二项就是结果
- 最小化就是最大化财政
- 如何满足多个先决条件?
- 如果只满足了部分先决条件,则会存在 \(A\to B\) 的无穷边
- 算法保证不会出现这种情况
open-pit mining

baseball elimination
- 判定冠军最有可能是谁
- 信息:当前输赢信息,还需要和谁比几场
- 发现:判定和如下信息有关
- 当前输赢
- 接下来要和谁打
- 判断 4 是否还有机会胜利
- \(w_i\):队 \(i\) 已经赢得的比赛数量
- \(r_i\):队 \(i\) 还剩下的比赛数量
- 队 4 如果接下来全胜,则赢得的比赛数量 \(w_4+r_4\)
- 其他队应该都要比 \(w_4+r_4\) 小
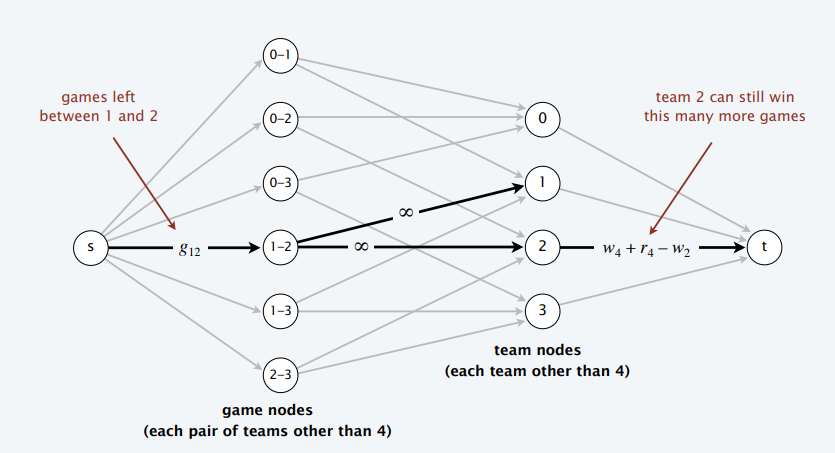
- s 出来的边都被饱和了 \(\Leftrightarrow\) 4 还有机会赢
- 如果存在最大流,则说明比赛都比完了,而且满足了队 4 赢最多的要求
HR 定理

- 在一个集合中,他们赢得的总数+内部还需要比赛的场数,如果他们算出来的平均胜利场数大于 \(w_z+g_z\),则该球队没戏了
- \(\Rightarrow\):上面的说法
- \(\Leftarrow\):max-flow
- 最小割不包含无穷边
- 比赛节点 \(x-y\in A\) \(\Rightarrow\) 球队节点 \(x,y\in A\)
- max-flow
- 球队节点 \(x,y\in A\) \(\Rightarrow\) 比赛节点 \(x-y\in A\)
- 否则将其加进来之后能够增流 \(g_{xy}\)
- 如果没戏,则最大流未满足 \(s\to\cdot\)
- 最小割不包含无穷边
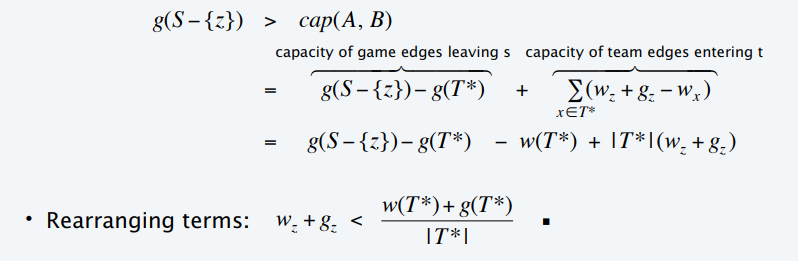
- \(S\):球队
- \(T^{\ast}\):\(A\) 中的球队